TRIGONOMETRY WITH RIGHT TRIANGLES: USING TRIGONOMETRY RATIOS TO FIND A SIDE OF A TRIANGLE
 |
Unit Overview
In this unit, students will use Trigonometry ratios to find a missing side given one of the acute angles of a right triangle.

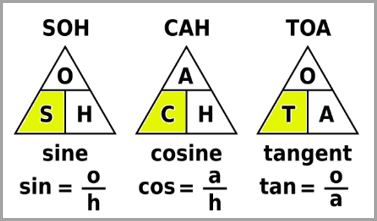
Using Trigonometry Ratios to Find a Side of a Triangle
The trigonometry ratios can be used to find many types of information, and one of their main purposes is to help solve triangles. To solve a triangle means to find the length of all the sides and the measure of all the angles. There are three main steps to help you find the side lengths of a triangle:
You will choose either sine, cosine, or tangent by determining which side you know and which side you are looking for.
Substitute your information into the trigonometry ratio.
Solve the resulting equation to find the length of the side. |
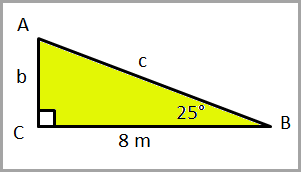
Example - Find b in the triangle below.
 |
Step 1: Choose the correct trigonometry ratio to use.
First, we know we must look at angle B because that is the angle we know the measure. So, looking at angle B, we want to identify which sides are involved. We know one side is 8m, and that side is adjacent to angle B. The side we're looking for is opposite angle B. So we need to choose the trigonometry ratio that has opposite and adjacent. We need to use the trigonometry ratio of tangent.
Step 2: Substitute.
Next, we write our trigonometry ratio: tan B = opposite/adjacent
Then, we substitute in the angle and the side we know: tan 25° = b/8
Step 3: Solve.
Now move the 8 to the other side by multiplying both sides by 8: 8* tan 25° = b
Use a calculator to find the answer. b = 3.7 m.
Let's Practice – Find a Side of a Triangle
1.) Identify all three step in order to find c in the triangle below.
|
Summary
Watch the video below in order to complete some practice problems.
Here are few reminders in order to find a side in a right-angled triangle using trigonometry.
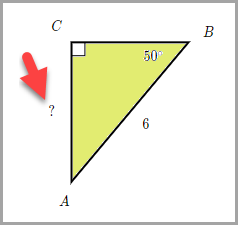
Example - Given r ABC, find AC.
Step 1: Determine which trigonometric ratio to use.
Focus on angle B since that is the angle that is given in the diagram. Note that we are given the length of the hypotenuse, and we are asked to find the length of the side opposite angle B. The trigonometric ratio that contains both of those sides is the sine.
Step 2: Create an equation using the trig ratio sine and solve for the unknown side.
Sin (B) = opposite/hypotenuse
Step 3: Substitute.
Sin (50°) = AC / 6
Step 4: Solve.
Multiply both sides by 6.
6 sin (50° ) = AC
4.60 ≈ AC
Let's Practice - Summary
2.) Determine which trigonometry ratio to use for the following triangle in order to find the missing side length of a.
|
3.) Determine which trigonometry ratio to use for the following triangle in order to find the missing side length of a.
|
| |
|
5.) Given rDEF, find DE.
|
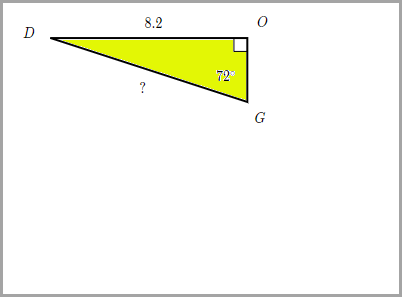
6.) Given rDOG, find DG.
 |
7.) Given rTRY, find TY.
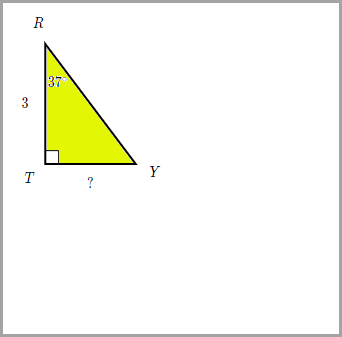 |
8.) Look at the triangle below and find the side BC.
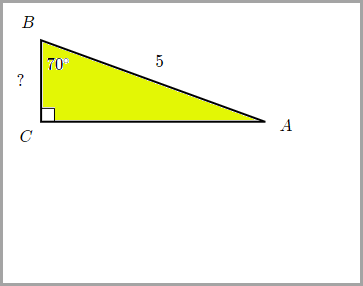 |
9.) Look at the triangle below and find the side AB.
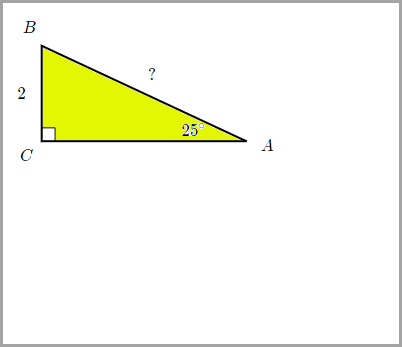 |
10.) Look at the triangle below and find the side AC.
|
 |
 Click on the icon to the left to practice solving for a side in right triangles. Click on the icon to the left to practice solving for a side in right triangles. |
| Practice 1: Using Trigonometry to Find Lengths |