CIRCULAR TRIGONOMETRY
 |
Unit Overview
This unit reviews angles and angle measurement. You will review special right triangles and apply them to the study of circular trigonometry.
Angle Measurement
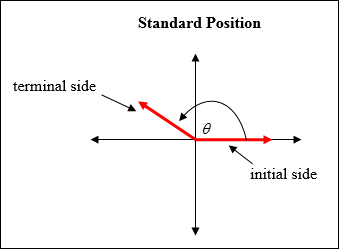
In a plane, an angle is formed by rotating a ray, called the initial side of the angle, around its endpoint until it coincides with another ray called the terminal side. An angle is in standard position if the vertex is at the origin and its initial side is along the positive x-axis.
 |
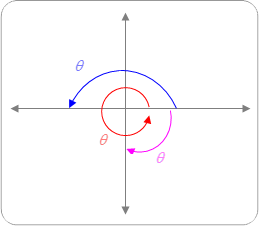
The measure of an angle in standard position is the amount of rotation from the initial side to the terminal side. If an angle rotates counter clockwise, the measure is positive. If the angle rotates clockwise, the measure is negative. *One rotation is equal to 360º.
 |
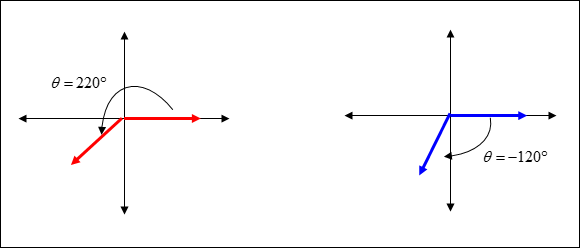Two angles in standard position are coterminal angles if they have the same terminal side.
| Example #1: |
 |
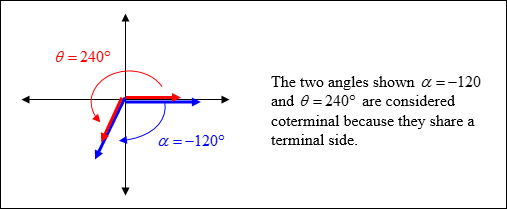To find coterminal angles to a given angle such that –360° < θ < 360°, add or subtract 360° to the given angle until the coterminal angles satisfy the given condition of –360° < θ < 360°. |
| Example #2: Find all coterminal angles such that –360° < θ < 360° for 560°. |
 |
Stop! Go to Questions #1-5 about this section, then return to continue on to the next section.
Reference Angles
For any angle θ in standard position, the reference angle θref is the positive acute angle formed by the terminal side of θ and the nearest part of the x-axis.
The reference angle of any angle can be found using the following:
 |
If the terminal side of θ is in quadrant III, then The reference angle of any angle can be found using the following:
 |
| Example #1: |
 |
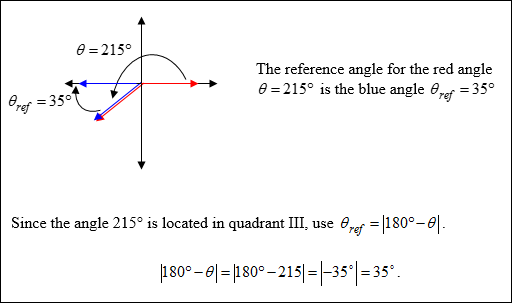Trigonometric Values (07:08) Stop! Go to Questions #6-9 about this section, then return to continue on to the next section.
Degree and Radian Measures
Degree measure of angles is used extensively in engineering, surveying and navigation. Another unit of angle measure is called the radian, which is better suited for certain mathematical development, scientific work and engineering applications.
The radian measure of an angle is equal to the length of the arc on the unit circle (a circle centered at the origin with a radius of 1) that is intercepted by the angle in standard position. The circumference of any circle is 2πr, where r is the radius of the circle. So the circumference of a unit circle is 2π(1) or 2π radians. Therefore an angle representing one complete revolution of the circle measures 2π radians or 360°. Thus, an angle of 180° = π radians and 90° =
. |
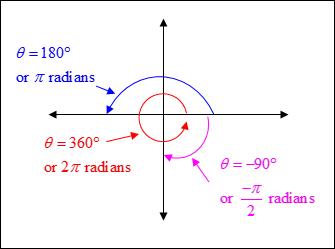You can convert from degrees to radians and visa versa.
 |
| Example #1: Convert 40° from degrees to radians and radians to degrees. |
 |
Example #2: Convert  radians to degrees. |
 |
Stop! Go to Questions #10-17 about this section, then return to continue on to the next section.
Circular Trigonometry
Trigonometry is the study of angles and triangles. The word trigonometry comes from the Greek words for “triangle measure Angles whose measures are multiples of 30° and 45° are commonly used in trigonometry. These angle measures are equivalent to radian measures of
and 
, respectively. The critical values in Quadrant I are as follows:
 |
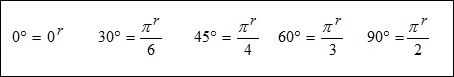If you remember that 180° = π radians, it is easy to remember the other angles.
 |
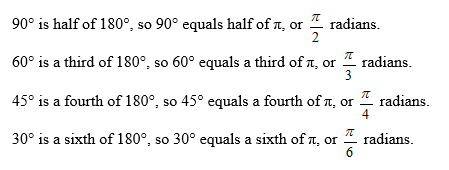In addition all whole number multiples will also be critical values for all angles ≤ 360°.
For example:
 |
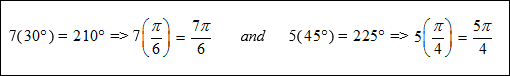The unit circle with critical values labeled in radian and degrees angles is shown below:
 |
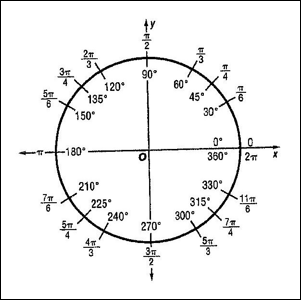The trig (short for trigonometry) ratios sine(sin), cosine (cos) and tangent (tan) are based on properties of right triangles. These three ratios are the most common trig ratios.
 |
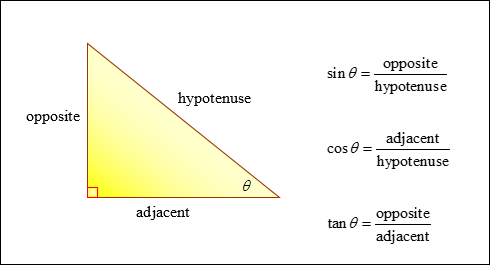There are certain angles whose exact trig functions can be found without a calculator. These angles are 30°, 45°, 60°, and any angle having any of these three as reference angles. The ratios of the lengths of the sides of each triangle is shown below. Throughout this unit, it will be helpful for you to learn the exact values of sin, cos, and tan of these angles.
 |
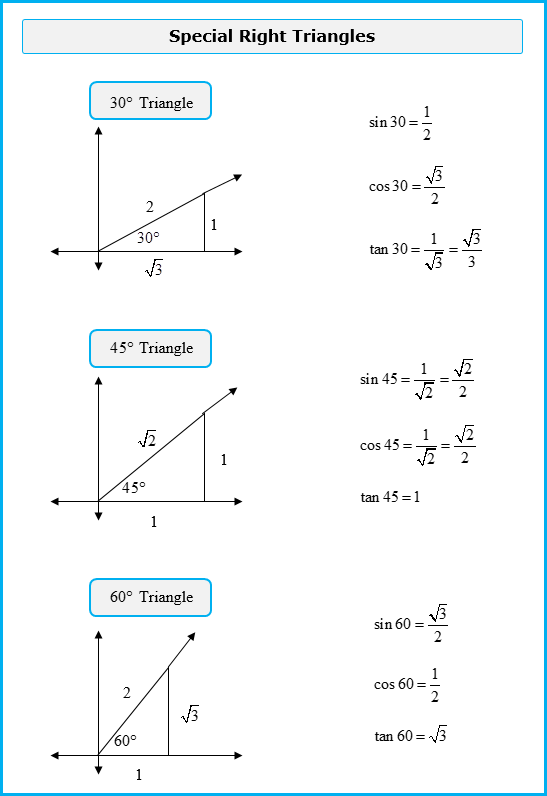Six Trig Functions (02:33)
Six Trig Functions and More (12:13)
Solving Right Triangles (04:15)
Special Right Triangles (04:25)
Polar Coordinates: Radar Blips (05:12)
Right Triangles in Quadrant 1
In the circle diagram below, a right triangle can be inscribed in the circle in the following manner. For an angle in standard position, the terminal side of an angle in the unit circle hits at a point whose x-coordinate is the angle’s cosine and whose y-coordinate is the angle’s sine, that is cos θ = x and sin θ = y.
 |
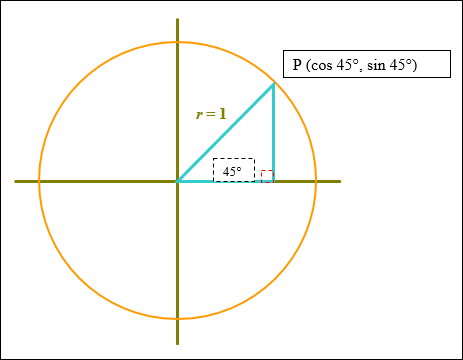In the above diagram, the hypotenuse of the triangle is also the radius of the circle. If we allow r = 1 and select one of the special right triangles to be inscribed in each quadrant of the circle, the trigonometric values can be established for each critical value from 0r to 2πr.
Example #1: Find the exact values of the sin |
 |
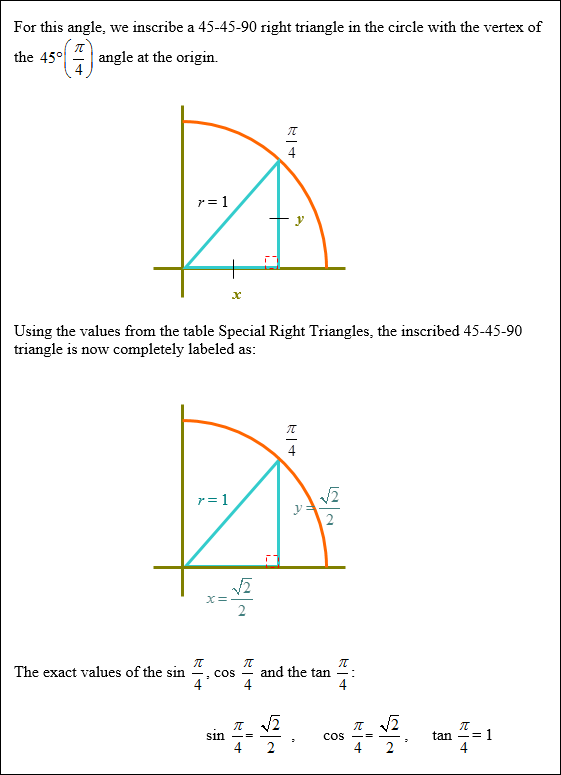Example #2: Find the exact values of the sin |
 |
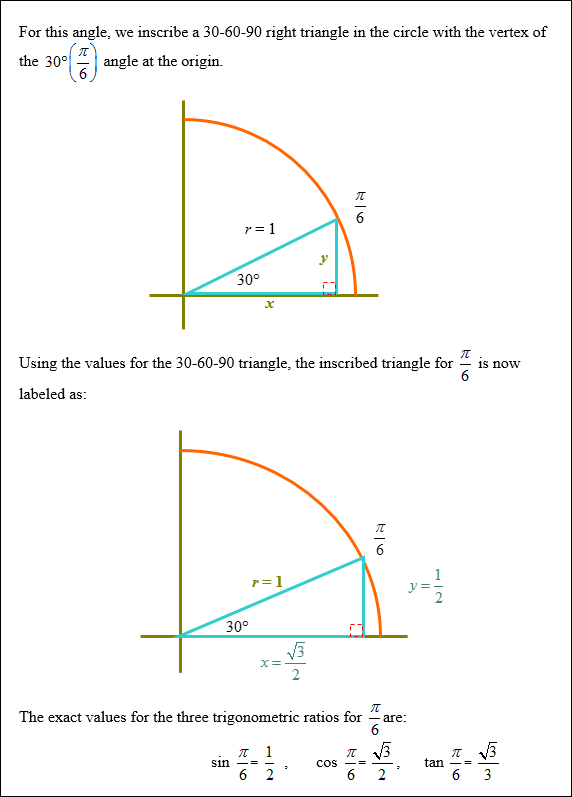Polar Coordinates: Radar Blips (05:12)Stop! Go to Questions #18-20 about this section, then return to continue on to the next section.
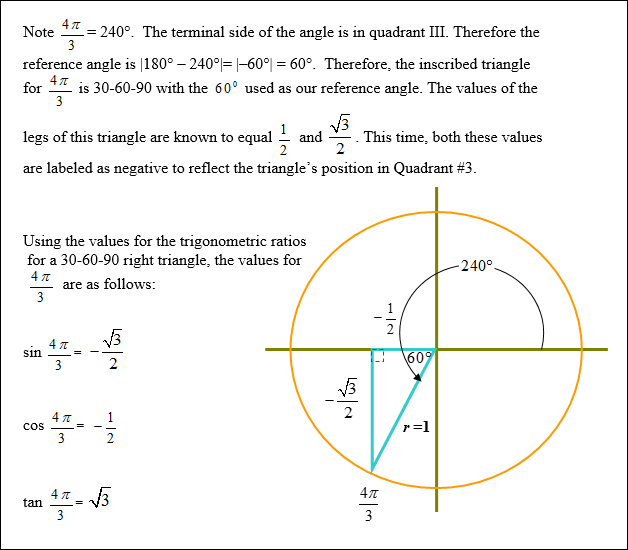
Right Triangles and Reference Angles in Quadrants #2, 3, 4
As the special right triangles are inscribed in quadrants #2, 3, and 4, the legs of the triangles take on values to reflect the direction taken in order for the radius (hypotenuse) to intersect the critical value on the unit circle.
Example #1: Find the exact values of the sin |
 |
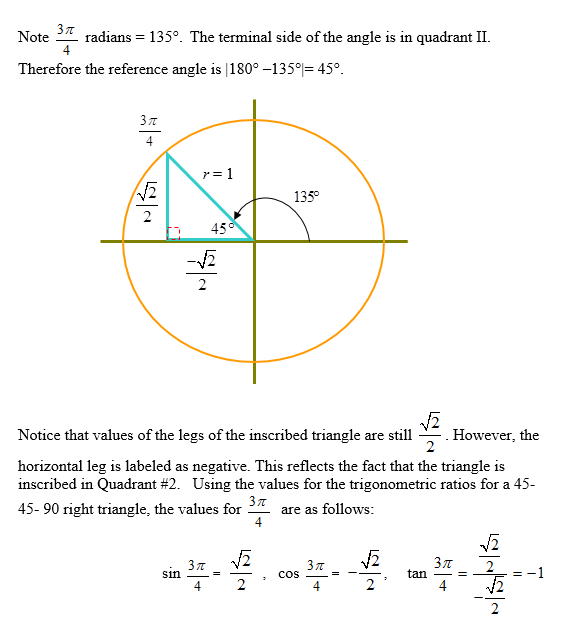, cos The chart below summarizes the signs of the trigonometric ratios for each quadrant.
 |
Example #2: Find the exact values of the sin |
|
, cos 
Example #3: Find the exact values of the sin |
 |
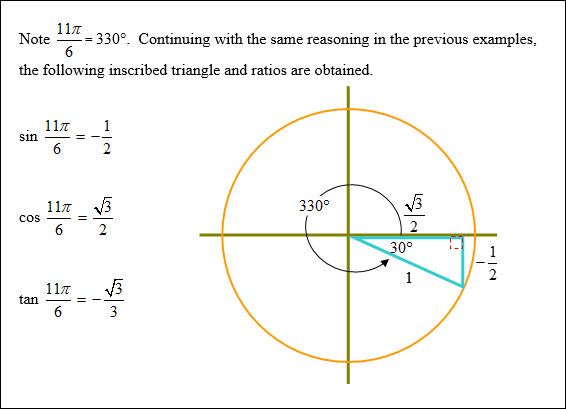, cos The Unit Circle (07:07) Stop! Go to Questions #21-38 about this section, then return to continue on to the next section.
Trigonometric Ratios for Quadrantal Angles
If the terminal side of an angle in standard position coincides with one of the axes it is called a quadrantal angle. In the previous discussion, inscribed triangles were used to evaluate the trigonometric ratios of the angles found in each quadrant of the unit circle. However, the angle measures of 0,
, π
, and 2π (0°, 90°, 180°, 270°, 360°) are not found “inside” any of the Quadrants # 1, 2, 3, or 4. Each of those angle’s position on the unit circle is found on either the x or y-axis which are the boundary lines between the four quadrants.  |
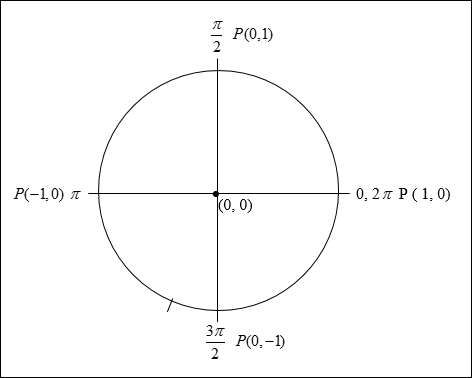It is easy to find the trigonometric ratios for these angles since the terminal sides lie along an axis.
Example #1: Find the exact values of the sin |
 |
Stop! Go to Questions #39-50 to complete this unit.