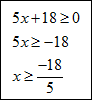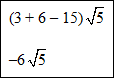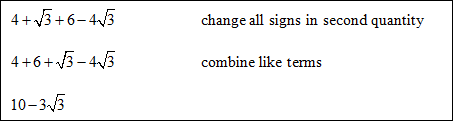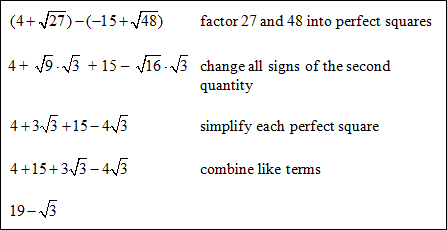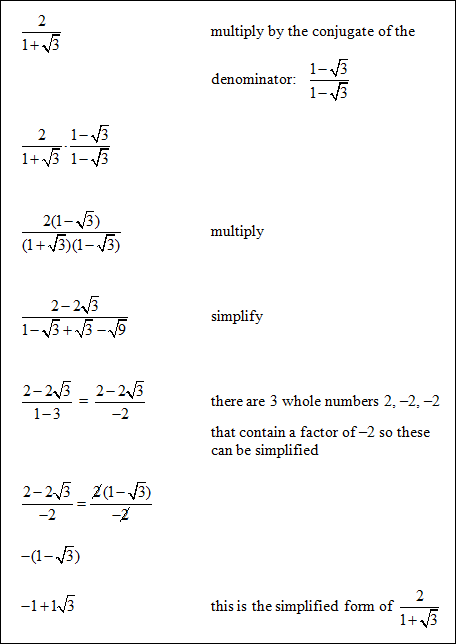PDF
RADICAL EXPRESSIONS AND EQUATIONS
Unit Overview
In this unit you will learn to simplify and manipulate radical expressions so that you can solve radical equations. You will also examine the rational exponents and how they relation to radical expressions.
Domain of a Square Root Function
The domain of a function is the set of all real-number values of x; therefore, the domain of a square root function,
f (x) = 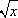 , does not include negative numbers. , does not include negative numbers.
To find the domain:
| 1.) set the numbers under the radical sign ≥ to 0 |
| 2.) solve the inequality |
| 3.) the result will be your domain |
Example #1: Find the domain of h(x) = 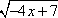 . .
|
Example #2: Find the domain of g(x) = 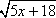 . .
The domain of g(x) is all x-values greater than or equal to 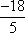 . . |
Stop! Go to Questions #1-4 about this section, then return to continue on to the next section.
Simplifying Radical Expressions
In the expression 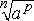 the the 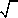 is called the radical, n is the index, a is the radicand and p is the power. is called the radical, n is the index, a is the radicand and p is the power.
To simplify:
| -divide p by n, this is the exponent of the variable outside the radical sign. |
| |
| -if there is a remainder, this is the new exponent of the variable under the radical sign. |
You may want to remember that when you have an even index, the answer is either positive or negative. Such as 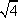 = ±2. When this is required, we use an absolute value symbol. In this unit you may want to only consider the positive square root. For example, = ±2. When this is required, we use an absolute value symbol. In this unit you may want to only consider the positive square root. For example, 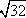 = = 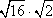 = = 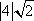 . However, for our purposes, we will not be concerned with the absolute value notation on even roots. This will become more significant in later courses. . However, for our purposes, we will not be concerned with the absolute value notation on even roots. This will become more significant in later courses.
Example #1: Evaluate 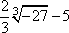 . .
|
Example #2: Evaluate 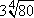 . .
|
Example #3: Evaluate 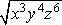 . .
This is a square root and the index is a 2. When an index is not written in a radical, it is understood to be an index of 2.
Divide each of the exponents by the index 2. This will be the new exponent of the variable outside of the radical.
|
Since there was a remainder of 1 when the exponent 3 was divided by the index 2, there is still an x inside the radical sign. |
Example #4: Evaluate 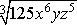 . .
Since the index is odd, we do not have to worry about absolute value signs.
Take the cubed root of 125 and divide each of the exponents by 3. Any remainders will stay inside the radical sign.
|
*If the radicand is not a perfect root, then we will factor it into perfect roots, if possible. |
Example #5: In 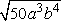 , 50 is not a perfect square root; but it can be factored using a perfect square root. , 50 is not a perfect square root; but it can be factored using a perfect square root.
|
Example #6: In 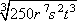 , 250 is not a perfect cubed root, but it can be factored using a perfect cubed root. , 250 is not a perfect cubed root, but it can be factored using a perfect cubed root.
|
 Squares and Square Roots (01:52) Squares and Square Roots (01:52)
 Higher Roots (05:09) Higher Roots (05:09)
Stop! Go to Questions #5-13 about this section, then return to continue on to the next section.
Product and Quotient Properties of Radicals
If a term has a rational exponent, it can be rewritten in radical form in the following way.
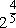 can be rewritten as can be rewritten as 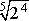 . . |
You can see that the numerator became the exponent of the radicand and the denominator became the index. |
This process can be reversed.
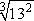 can be written using a rational exponent as can be written using a rational exponent as 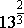 . . |
Example #1: Find the product of 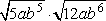 . .
|
Example #2: Find the quotient of 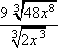 . .
|
 Fractional Exponents (06:21) Fractional Exponents (06:21)
Stop! Go to Questions #14-17 about this section, then return to continue on to the next section.
Adding and Subtracting Radicals
To add or subtract radicals:
1.) they must have the same index |
| |
2.) they must have the same radicand |
| |
3.) add or subtract the numbers in front of the radical term |
Example #1: Compute: 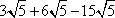 . .
*When adding or subtracting numbers and radicals, you want to combine like terms. |
Example #2: Find the difference: 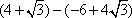 . .
*If the radicands are not the same in an addition or subtraction problem, check to see if they can be simplified into common radicands. |
Example #3: Find the sum.
|
Example #4: Find the difference.
|
Stop! Go to Questions #18-20 about this section, then return to continue on to the next section.
Multiplying Radicals
Example #1: Find the product.
|
Stop! Go to Questions #21-22 about this section, then return to continue on to the next section.
Rationalizing the Denominator
If a rational expression contains a radical in the denominator, it is not completely simplified. A process called rationalizing the denominator is used to eliminate the radical from the denominator. We used a similar process in a previous unit when we simplified expressions containing complex numbers. If you remember, we used a process call the conjugate of the denominator. The same process is used for radical expressions. Let’s first review how to find the conjugate of a complex number.
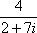 would have a conjugate of 2 – 7i because you use the opposite sign. would have a conjugate of 2 – 7i because you use the opposite sign.
|
| |
To simplify this expression you would multiply it by 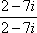 . . |
Let’s look at a radical expression now.
Example #1: Simplify by rationalizing the denominator.
|
Stop! Go to Questions #23-27 about this section, then return to continue on to the next section.
Solving Radical Equations
| One Radical Term |
| |
| -isolate the radical term |
| |
| -square or cube both sides (depending on what the index is) |
| |
| -solve and check |
| Two Radical Terms |
| |
-make sure that the radicals are on opposite sides of the equal sign, one on each side |
| |
-square or cube both sides (depending on what the index is) |
| |
| -solve and check |
Let’s try another example.
Stop! Go to Questions #28-31 to complete this unit.
|