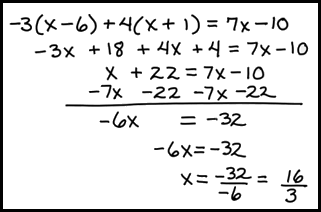
SOLVING EQUATIONS, PART 1
|
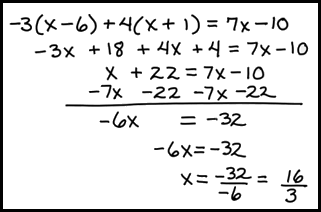Unit Overview
In this unit, students will be able to solve and check multi-step, one-variable linear equations.
Key Concepts
Introduction
Solution: any number(s) substituted in for the variable that makes an equation true
Look at these examples to determine if x = 4 is a solution.
x + 2 = 6
4 + 2 = 6 ?
Yes, 4 is a solution.
5x – 8 = 10
5 • 4 – 8 = 10 ?
12 = 10 ?
No, 4 is not a solution.
Look at these examples to determine if y = 5 is a solution.
3(2y + 1) – 5 = 3y + 10
3(2 • 5 + 1) – 5 = 4 • 5 + 8 ?
28 = 28 ?
Yes, 5 is a solution.
3y2 – 8y + 7 = 10
3 • 52 – 8 • 5 + 7 = 10 ?
42 = 10 ?
No, 5 is not a solution.
Let's practice. Determine if the given value is a solution for the equation.
|
 Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
PROPERTIES OF EQUALITY TO SOLVE 1-STEP EQUATIONS
A key step to solve most any algebraic equation is the property of equality, which allows one to perform the same operation to both sides of equation. This method is used to get the variable by itself on one side of the equation by eliminating constants and coefficients. Use the inverse operation to eliminate those numbers.
Look at these basic examples that illustrate the four properties of Equality:
 |
While those above examples may be relatively easy to solve mentally, many algebraic equations are much more complex, but can be solved using these basic Properties of Equalities.
SOLVING 2-STEP EQUATIONS
When solving 2-step equations, you should use the addition and subtraction properties of equality before applying the multiplication and division properties of equality.
Look at these examples that correctly and incorrectly apply the properties of equality.
CORRECT METHOD (using the subtraction property of equality prior to the division property):
2x + 4 = 10
2x + 4 – 4 = 10 – 4
2x = 6
2x ÷ 2 = 6 ÷ 2
x = 3
3 checks out as a solution:
2 • 3 + 4 = 10?
10 = 10
INCORRECT METHOD (using the division property of equality prior to the subtraction property):
2x + 4 = 10
2x ÷ 2 + 4 = 10 ÷ 2
x + 4 = 5
x + 4 – 4 = 5 – 4
x = 1
1 does not check out as a solution:
2 • 1 + 4 = 10?
6 ≠ 10
Also be careful when dealing with negative constants and coefficients, along with decimals and fractions. Look at this example.
-5d – 32.6 = -12. 8
-5d – 32.6 + 32.6 = -12. 8 + 32.6
-5d = 19.8
-5d ÷ (-5) = 19.8 ÷ (-5) *put negative #s in parentheses when multiplying
d = -3.96 or dividing to avoid confusing with subtraction
Use your calculator to check your solution:
-5 • (-3.96) – 32.6 = -12. 8
19.8 – 32.6 = -12. 8
-12.8 = -12.8
Click on the video for a further explanation and practice:
Let's practice. Determine the solution for each equation.
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
SOLVING EQUATIONS WITH VARIABLES ON BOTH SIDES
If variables are on both sides of equations, apply the addition or subtraction property of equality to eliminate the variables on one side of the equation.
Look at this example applying the subtraction property of equality.
6x + 12 = 2x – 40
6x – 2x + 12 = 2x – 2x – 40
4x + 12 = -40
4x + 12 – 12 = -40 – 12
4x = -52
4x ÷ 4 = -52 ÷ 4
x = -13
Use your calculator to check your solution: 6(-13) + 12 = 2(-13) – 40
For efficiency, many students prefer to write each property of equality under the previous step when solving any type of equation. It may be helpful to draw a line through the equal signs to show the property being done to both sides of the equation.
Here is the previous example done using this method.
6x + 12 = 2x – 40
-2x -2x
4x + 12 = -40
-12 - 12
4x = -52
÷ 4 ÷ 4
x = -13
Look at this next example applying the addition property of equality.
-4x – 32 = -9x + 82.6
+9x +9x
5x + 32 = 82.6
+32 +32
5x = 114.6
÷ 5 ÷ 5
x = 22.92
Use your calculator to check your solution:
-4(22.92) – 32 = -9(22.92) + 82.6
-123.68 = -123.68
Click on the video for a further explanation and practice:
Let's practice. Determine the solution for each equation.
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
SOLVING MULTI-STEP EQUATIONS
In some cases, you may have simplify a side by eliminating parentheses (using the distributive property) and/or combining like terms.
Look at this example of solving a multi-step equation.
6(2x – 3) – 8x + 4 = 70
6(2x – 3) – 8x + 4 = 70 *Eliminate parentheses by using the distributive property
12x– 18 – 8x+ 4 = 70 *combine like terms on the left side
4x– 14 = 70 *finish solving the equation
4x – 14 + 14 = 70 + 14
4x = 84
4x ÷ 4 = 84 ÷ 4
x = 21
Use your calculator to check your solution:
6(2 • 21 – 3) – 8 • 21 + 4 = 70?
70 = 70
Click on the video for a further explanation and practice:
Let's practice. Determine the solution for each equation.
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
ADVANCED MULTI-STEP EQUATIONS
For any complex equation, follow these steps:
1. Eliminate parentheses by using the distributive property
2. Simplify each side by combining like terms
3. Get the variables on the same side (use the addition or subtraction property of equality)
4. Get the variable by itself using the inverse of the properties of equalities
Look at this next example applying these steps.
2(3x + 4) – 2 + 8x = 4x + 73
2(3x + 4) – 2 + 8x = 4x + 73 *Eliminate parentheses by using the distributive property
6x+ 8 – 2 + 8x = 4x + 73 *Combine like terms on the left side of the equation
14x+ 6 = 4x + 73
-4x -4x *Get the variables on the same side
10x + 6 = 73
-6 -6 *Get the variable by itself
10x = 67
÷10 ÷10
x = 6.7
Use your calculator to check your solution:
2(3 • 6.7 + 4) – 2 + 8 • 6.7 = 4 • 6.7 + 73
99.8 = 99.8
Click on the video for a further explanation and practice:
Let's practice. Determine the solution for each equation.
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
