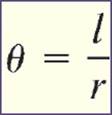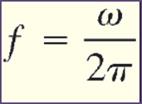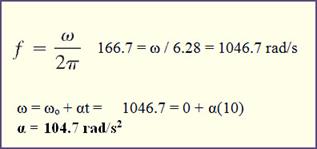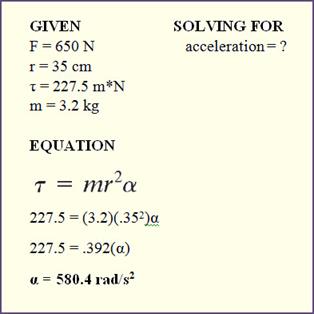
ROTATIONAL MOTION
Unit
Overview
During
this unit, we will discuss velocity and acceleration of different points moving
along a circular, rotating object. Later in the unit we will also see how
forces affect objects moving in a circular motion to create acceleration.
Rotational
Motion, Angular Quantities
During
this chapter we will be referring to objects that travel in a circular motion
as being a rigid rotating object. We
call it a rigid object because we are assuming that its shape is never
changing. Sometimes when forces act on an object, the shape can be deformed,
but most of the time it is so small that it will not affect the overall system
of the rotating object.
During
rotational motion, all points on the object move in circles around the axis of rotation. The axis of rotation
is referring to the center of the circle. The radius of the circle will be
written as the symbol r. Any point along
a circle with the same radius will sweep out equal angles in the same amount of
time. In physics it is common to refer to an angle as a radian when talking
about rotational motion.
|
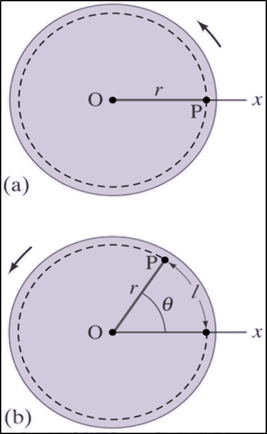
A radian is defined as the angle
subtended by an arc whose length is equal to the radius. If the arc length
and the radius are the same, that is equal to 1 radian. This yields the
equation:
where l
is the arc length. |
The picture below shows a point “P” on a
circle rotating around the axis of rotation “O”, the distance along the arc of
the circle that “P” travels is the arc length “l”
When
talking about the radian, it does not have any units because it is a ratio of
two lengths. But when given an angle in radians, it is best to write rad after it to remind us that it is not
in degrees. Radians are however related to degrees.
|
A
complete circle has 360 degrees, which is the same as an arc length equaling
the circumference of a circle, so l =
2pr2
and since θ = l/r we can substitute 2pr2 in for l and get 2π rad in a complete
circle, so 360° = 2π rad One radian is then equal to 360/2π = 57.3° An
object that has completed one complete revolution has rotated through 360° or
2π rad. |
|
Examples: |
|
1. A car tire rotates 6.7 revolutions.
How many radians has it rotated? |
|
Knowing
that 1 revolution = 360 degrees = 2π rad, we can just convert to the
units needed 6.7 revolutions (2π rad / 1 rev) = 13.4π rad = 42.1 rad OR 6.7
(360) / 57.3 = 42.1 rad - knowing that there are 57.3 degrees
per radian, you can simply divide the total degrees traveled along the circle
and divide it by 57.3 degree. |
|
|
|
A bird’s eye can distinguish objects
that have an arc angle no smaller than 3 X 10-4 rad. a)
How many degrees is
this? b)
How small of an
object can the bird distinguish when flying at a height of 100m? c)
Convert 3 X10-4 radians to degrees 3 X10-4 (360°/2π rad) = .017° d)
In this problem, we know that the radius is 100m and the
θ is 3 X10-4 radians we can use the equation θ = l/r so 3 X10-4(100) = .03 m
or 3 cm. |
|
|
Angular velocity and acceleration
Velocity
and acceleration for a rotating object mean the same thing as it did in unit 2
for an object moving along a linear path. For angular velocity, because it is
now angular displacement divided by time, we will use the change in angular
displacement which is where θ1
is the initial angle and θ2 is the final angle.
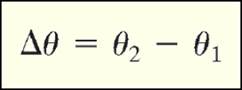
The
picture below shows how the change in angular displacement is found.
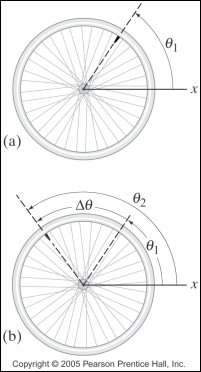
The
angular velocity will be written
with the Greek lowercase omega symbol, ω. The equation for angular
velocity is then written as
ω = Δθ /
Δt
Angular
velocity has units of radians/second (rad/s). One thing to remember is that all
points along a rigid rotating object will rotate with the same angular
velocity, because every position on the object moves through the same angle per
same amount of time.
Just
like linear velocity, an object can have a negative velocity if traveling west
or south. With angular velocity, an object is considered positive if it is moving in a counterclockwise
direction and negative if it is
moving clockwise.
Angular acceleration is written with the
Greek lowercase letter alpha (α). Angular acceleration is the change in
angular velocity divided by the amount of time needed to make this change.
Which gives us the equation:
![]()
Since
ω is the same for all points on a rotating object, α will also be the
same for all points and angular acceleration will be expressed as rad/s2.
A
point traveling along a rotating object will have an angular velocity, as well
as a linear velocity. If you remember from our unit on circular motion, an
object traveling in a circular path has a velocity that is tangent to the
circle. That is the same in this case when talking about linear velocity.
Because it is tangent, we can solve for linear velocity by using the following
equation:
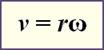
By
examining the equation, we can see that the further away from the axis of
rotation, the greater the linear velocity will be. This is not true for angular
velocity, remember that angular velocity
is the same for all points traveling along the same rotating object.
The
picture below shows how linear and angular velocities are related
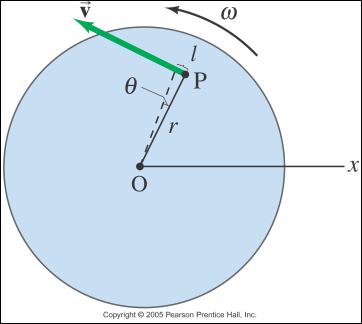
The
next picture shows how linear velocity increases as you move further away from
the axis of rotation.
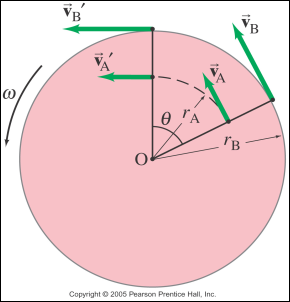
If
a rotating object contains a linear velocity, it must also contain a linear
acceleration. Linear acceleration however is a little more complicated than
linear velocity. There is a linear acceleration vector that points tangent to
the path of the circular motion just like linear velocity does. There is also a
radial acceleration pointing towards the center of the circle (like we saw in
our unit on circular motion). Radial acceleration is also called centripetal
acceleration. So with these two types of acceleration, total linear
acceleration is the vector sum of these two components.
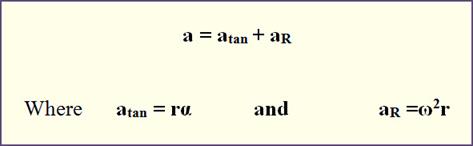
Centripetal (radial) acceleration depends on radius, therefore the
further the point is from the axis of rotation, the greater centripetal
acceleration it will feel.
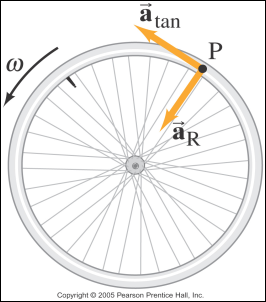
The picture below shows the direction of the atan and aR
vectors
|
Example |
|
1. A merry-go-round is
initially at rest, after being pushed it obtains an angular acceleration of
.060 rad/s2 which increases its angular velocity for 8.0 seconds.
At the end of the 8 seconds determine the
|
|
GIVEN
SOLVING
FOR time = 8 s angular velocity anfular acceleration = .06 rad/s2 a.
α = Δω/Δt .06 = ω/8
ω = .48 rad/s |
|
b. GIVEN – the radius of the child is 2.5 m v = rω v
= (2.5)(.48) v = 1.2 m/s |
|
c.
atan = rα atan = (2.5)(.06)
atan = .15 m/s2
|
|
d. aR =ω2r aR = (.482)(2.5) aR = .58
m/s2 |
|
e. When finding the
total acceleration, we know that it is a vector sum of atan and aR
and looking at the direction that these two vectors point along a
circle, we can see that they are perpendicular to one another. Therefore in
order to find the vector sum, we need to find the hypotenuse of the right
triangle that they form. So… atotal2
= atan2 + aR2 a
total2 = .152 + .582 a
total2 = .3599 atotal
= √.3599 atotal2
= .60 m/s2 |
|
|
Frequency
and Period
In
our unit about circular motion we learned that frequency is equal to the number of revolutions per second. In this
chapter we can relate angular velocity to frequency by thinking of it in terms
of radians. One revolution corresponds to an angle or 2π radians.
|
Therefore
1 rev/s = 2π rad/s which will yield the equation:
Don’t
forget the unit for frequency is the Hertz (Hz). The
time required for one revolution is known as the period and is the inverse of frequency. So T = 1/f because
period is an amount of time, its units are the second. |
|
Example |
|
1. A CD rotates at 6800 rpm
(revolutions per minute) what is the angular velocity of the CD? |
|
|
|
|
Constant
Angular Acceleration
In
unit 2, we learned the kinematics equations that we have used countless times
throughout all units thereafter. These equations relate displacement, time,
velocity and acceleration, assuming acceleration is constant. These same types
of equations can be written in terms of angular displacement, time, angular
velocity and angular acceleration assuming angular acceleration is constant. A
main difference between them is that displacement (x) is replaced by radians
(θ), v is replaced by ω, and a is replaced with α. Below is a
chart that shows both linear kinematics equations alongside angular equations.
You can see that they are very similar.

|
Example 1 |
|
1. A motor accelerates from rest to
10,000 rpm in 10 seconds, what is the average angular acceleration? |
|
|
|
In
order to find acceleration, we first need to solve for final angular velocity
and then plug it in to find angular acceleration. |
|
|
|
Example 2 |
|
A car engine slows from a frequency of
75 Hz to 20 Hz in 2.5 seconds. Find the acceleration of the car’s engine. |
|
|
|
In
order to solve for acceleration, we need to take the frequencies and find the
initial and final angular velocities |
|
|
Torque
Just
like with linear motion, in order to get an object to move, a force is
required. For rotational motion it is also very important where the force is
applied as well as the direction of the force.
For
example, think of using a wrench. The longer the wrench, the more force can be
applied. The length at which the force is applied relative to the axis of
rotation is called the lever arm. When using something like
a wrench, the further away from the axis of rotation, the less force is needed
to move the object. In other words, not only does the amount of force matter,
but the angular acceleration is also proportional to the perpendicular distance
from the axis of rotation to the line along which the force acts (lever arm).
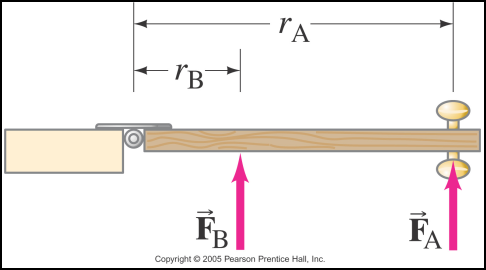
Below
is a picture showing two forces acting at two different distances. This is a
picture of a door on a hinge. And forces A and B are applied to open the door.
At distance rB it will take more of a force to open the door compared to
distance rA. Both forces are perpendicular to the lever arm.
The
angular acceleration then must be equal to the product of the force and the
lever arm. This product is known as torque. Torque is represented by the
Greek lowercase letter tau (τ).
Depending
on how a force is applied to create angular acceleration depends on the angle
at which it is applied. If force is perpendicular to the lever arm, it will be
the most effective. If it is at an angle, it will be slightly less
effective.
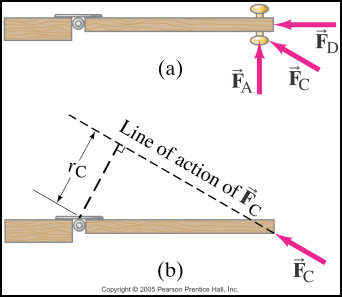
Below
is a picture of three different forces acting on a door in order to open
it, FA, FC and FD.
FA is acting perpendicular to the lever arm so it will need
the least amount of force. FC is acting at an angle. When a force
acts at an angle, the easiest way to figure out exactly how force is actually
used to cause an acceleration is to draw an imaginary line from the force
vector to the axis of rotation. Then another line from the axis of rotation to
the imaginary line in order to form a right angle. This is shown in picture B
below. The distance then between the axis of rotation and the imaginary
extension of the force vector is the actual lever arm distance being applied to
the object in order to cause an angular acceleration. As you can see from the
picture rC is much shorter than where the force is actually being
applied on the door. This shows how a force at an angle (FC) is less
effective than a force that is perpendicular. (FA). Now looking at
force FD, it is somewhat common sense that the door would not move
at all based on the location of the force.
Torque
is defined as the perpendicular distance (lever arm) times the amount of force.

So
if the force is at an angle, the
equation becomes τ = rF(sinθ) where
the θ is the angle between F and r. (HINT: you may have to draw a picture
to see which angle to use, the angle the problem gives you, or its
complimentary angle).
When
more than one torque acts on an object, the angular acceleration is
proportional to the sum of the torques. So if multiple torques are acting in
the same direction, we can add the torque together to find acceleration. If a
torque is acting in the opposite direction, we subtract the torques to find the
net torque. Once again, torque can be negative. If the net torque is applied to
accelerate the object in a counterclockwise direction, it is a positive torque.
If the net torque is applied to accelerate the object in the clockwise
direction, it is a negative torque.
Since
torque is related to force and when a force or torque is applied to an object
it causes an acceleration, it is easy to relate torque to Newton’s Second Law
of motion (F = ma).
![]()
The
quantity mr2 in the equation above is known as the rotational
inertia of a particle in motion. Since anything with mass has inertia
and it also depends on its location, we can relate it to Newton’s First Law in
terms of inertia (the tendency for objects to resist change). Depending on the
location of the mass m, an object can contain more than one rotational inertia,
if these masses are along the same object. In this case, you would just find
the rotational inertia for each mass and add them together. This then creates
its own equation: Where I is
rotational inertia. When there are many rotational inertias in a system, this
is used to find the net torque.
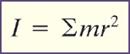
|
Example 1 |
|
1. You push on a door perpendicular to
the axis rotation with a force of 650 N at a distance of 35 centimeters from
the door. How much torque is applied to opening the door? |
|
|
|
Example 2 |
|
2. If the same door in example one has
a mass of 3.2 kg, how fast would the door accelerate? |
|
|
|
|
A
look ahead:
In
the next unit you will perform a laboratory investigation using a ladybug on a
marry-go-round in order to observe and calculate angular velocity and
acceleration of an object undergoing rotational motion.

Below are additional educational resources and activities for this unit.