
LINEAR MOMENTUM
Unit
Overview
During this unit, we
will learn how velocity and mass work together to provide an object with
momentum. Momentum also affects the rate at which objects are able to speed up,
or slow down. Depending on an objects momentum also determines what happens
during various types of collisions. These scenarios will be explored during
this unit.
Introduction
to Momentum
In
the previous unit we learned about the law of conservation of energy, and how
energy is not created or destroyed, only transferred from one form to another.
Besides energy, there are other quantities that are conserved, such as linear
momentum, angular momentum, as well as electric charge. Therefore it is important to remember that
momentum is conserved in a problem. If a collision take place where two objects
that both have momentum hit each other, the total amount of momentum of the
system will never will change. The velocities and masses of the two objects may
change, but their collective amount of momentum doesn’t change.
Momentum
is
defined as the product of an object’s mass and velocity. Momentum is
represented by the symbol p.
Therefore the equation that we will be using for momentum is:
P = mv (momentum = mass X velocity)
The
units for momentum are simply kg*m/s since we are multiplying mass and
velocity.
Because
velocity is a vector, momentum is also a vector, so it is important to think
about an object’s direction of motion (velocity is negative for an object
travelling west or south).
When
thinking about objects with momentum, it is fair to say that a faster moving
truck contains more momentum than a slower identical truck. Likewise a truck
that has more mass than a car traveling at the same speed will have more
momentum. Momentum depends on mass and velocity; therefore two objects of
different masses may have the same momentum as long as their velocities are
proportional. The more momentum an object has, the harder it is to change its
direction or slow it down.
Any
object with mass that is moving, has momentum. There are a lot of times when an
additional force acts on an object to change its momentum. This force acting
over a time period to change an object’s momentum is called impulse.
Impulse defines the rate of change of momentum in that a large force, will
result in a large change of momentum. Inversely the longer it takes to change
momentum, the less force acts on the object. There are many examples of how
impulse affects momentum. In other
words, the impulse tells us that we can
get the same change in momentum with a large force acting for a short time, or
a small force acting for a longer time. This relationship between
impulse and momentum is called the impulse-momentum
theorem.
Examples
of impulse:
- This is why you should bend your knees when you land
- why airbags work
- why landing on a pillow hurts
less than landing on concrete.
All of the above examples show
how an increase in time, before coming to a stop, will decrease the force of
impact.
The equation for impulse:
Impulse = force X time
A
force is required to change the momentum of an object; therefore the rate of change of momentum of an object
is equal to the net force applied to it. According to Newton’s 2nd
law (formally learned as F=ma) we can also apply this to momentum by deriving
the equation;
F = Δp/t (force = momentum /
time) ** remember the delta (Δ) means
change in …. Final – initial.
Another
way to write this equation in order to show all variables involved is written
below:
Ft = Δmv (force X time = change in mass X velocity)
In the following video the physics
tutor defines momentum, force, and impulse. Momentum has a magnitude and
direction, and is equal to the mass times the velocity. Force is defined as the
change in momentum over the change in time, while impulse is equal to the force
times the amount of time the force is applied.
|
Examples Problems |
|
1. A 54458 gram dog is running at a
speed of 12 m/s.
|
|
|
|
|
|
|
|
2. A 670 kg sports car starts at a
speed of 10 m/s and accelerates at a rate of 2 m/s2 for 7 seconds.
What is its momentum at the end of the 7 seconds? |
|
|
|
|
|
3.
A constant force of 1200 N is acting on a car for 40 seconds to slow
it down; the car has a mass of 4800 Kg, what is the change in velocity of the
car? |
|
|
|
** Since we are finding the change in velocity – we do not need
to worry about the initial – final. Whatever number we derive from the
equation will indicate how much the car has slowed down. **Velocity
slowed by 10 m/s |
Collisions
Outside
forces can be applied to objects to cause a change in momentum. Sometimes these
forces come from collisions between two or more objects, each containing their
own momenta. As we learned in the
beginning of the unit, momentum is conserved during a collision just like
energy was conserved in the previous unit. During a collision, velocity or mass
of the total system will change in order to have the same total momentum before
and after the collision of all objects involved. Because it is conserved, we yield the
equation:
pbefore = pafter or
![]()
Where Ma is the mass of object a, Va is
the velocity of object a. Likewise Mb is the mass of object b and Va is the
velocity of object b. It is important to remember that everything on the left
side of the equal sign is before the collision takes place, and everything on
the right side is after the collision occurs.
There
are three types of collisions that we are going to explore in this unit, they
are:
1.
elastic
2.
inelastic
3.
“explosions”
In
all cases of collisions, momentum is conserved. A big difference between
elastic and inelastic collisions is that kinetic energy is also conserved in
elastic collisions, but not during inelastic collisions.
Elastic
Collisions
During
an elastic collision the total amount of kinetic energy is the same before the
collision, as well as after the collision. Just like with momentum. During
these collisions, two objects will collide and then bounce back in opposite directions.
As seen in the picture below:
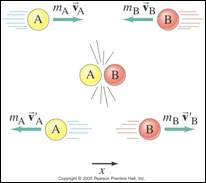
Don’t
forget that the equation for kinetic energy is KE = ½ mv2
Inelastic
Collisions
With inelastic collisions, some of the initial
kinetic energy is lost to thermal or potential energy. It may also be gained
during explosions, as there is the addition of chemical or nuclear energy.
Therefore KE is not conserved.
A completely inelastic collision is one where the
objects stick together afterwards, so there is only one final velocity.
The picture below shows an inelastic collision where
the bullet enters the box, and now they move together after the collision as a
system. When this happens we will add the masses of the bullet and the box to
find the final velocity after the collision, which is why kinetic energy is not
conserved.
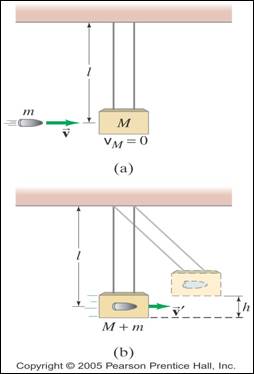
“Explosions”
An
“explosion” is a situation where there is an internal force acting on a system
to make it move.
For
Example:
–
Gun Powder
–
Firecracker
–
Rocket Propulsion
–
Momentum conservation works for a rocket as long as we consider
the rocket and its fuel to be one system, and account for the mass loss of the
rocket.
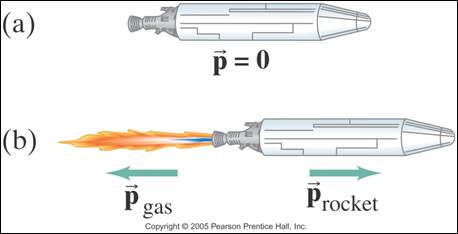
In
most linear explosion problems the object will contain two parts after the
explosion traveling in opposite directions. It is important to remember then
the direction of one of the particles will be negative, therefore giving it a
negative velocity.
In
an explosion problem, momentum and kinetic energy are conserved only after the
explosion, because they were at rest before the internal combustion. Therefore;
Pa = - Pb
•
In this case Pa = particle one after the explosion and Pb =
particle two after the explosion.
**
the momentum of the systems are equal in magnitude but opposite in direction**
(Newton’s Third Law)
|
Elastic Examples: |
|
1.
A ball with a mass of 883 grams is moving west at a speed of 3.4 m/s where it
hits another ball with a mass of 900 grams moving east at 5 m/s. If the first
ball moves east after the collision with a speed of 2.7 m/s, how fast and in
what direction does the second ball move? |
|
|
|
Inelastic Example |
|
1. A 6 kg fish swimming at 1 m/sec swallows a 2 kg
fish that is swimming towards it at 2 m/sec.
Find the velocity of the fish immediately after “lunch” |
|
|
|
“Explosion” Example |
|
1.
A cart with a mass of 3 kg is sitting next to a cart with a mass of 2 kg.
Between them is a compressed spring. When the spring is released, the 3 kg
cart moves at a speed of 5 m/s. How fast did the 2 kg cart move? |
|
|
|
**
I made the velocity of object a negative because we can assume that that one
of them will be moving west, and the other is moving east when the spring is
released. It really doesn’t matter if you make Va negative, or Vb negative, just
as long as you note that they will be moving in opposite directions. Because
both cars were at rest before the spring was released, they did not have any
momentum, so we only need to worry about what happened after the spring was
released. |
|
|
|
This
makes sense that Vb is a positive number because it would be moving east,
since object a moved west after the collision. |
A
Look Ahead
In
the next unit, you will perform a laboratory experiment to observe momentum and
the affects of different types of collisions based on an object’s mass and
velocity. We will mostly be looking at elastic and inelastic collisions in one
dimension. You will be able to observe how momentum and kinetic energy are
conserved for elastic collisions, and how momentum is conserved for inelastic
collisions.

Below are additional educational resources and activities for this unit.







