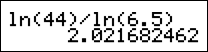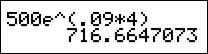Natural Logarithms

NATURAL LOGARITHMS

Unit Overview
In this unit you will evaluate natural exponential and natural logarithmic functions and model exponential growth and decay processes. You will also solve logarithmic and exponential equations by using algebra and graphs. Real world problems involving exponential and logarithmic relationships will be solved at the conclusion of the unit.

Natural Exponential and Natural Logarithmic Functions

The number e is an important irrational number. It is approximately equal to 2.71828. Like pi, the value is constant.

An exponential function with the base e is called a natural base exponential function. These functions are useful in describing continuous growth or decay. For example, the number e is used to solve problems involving continuous compound interest and continuous radioactive decay. Exponential functions with the base e have the same properties as other exponential function.

The natural logarithmic function y = log_e x is abbreviated y = ln x and is the inverse of the natural exponential function
y = e ^x.

Example #1: If e⁵ = 148.413, what is x in the expression ln x = 5?

e⁵ = 148.413
ln(148.413) = 5	Write the exponential as the inverse logarithm (ln).
∴ x = 148.413

*Note: The three triangular dots are an abbreviation for the word, “therefore”.

Example #2: If ln 54.598 = 4, what is x in the expression e^x = 54.598?

ln 54.598 = 4
e⁴ = 54.598	Write the exponential as the inverse logarithm (ln).
∴ x = 4

Let's practice changing exponential expressions of e to natural logarithms (ln), and vice versa. (Don't use a calculator; it's not necessary. Just follow the definition of the natural logarithm and how it relates to e.)

If e³ = 20.086, what is x in the expression ln x = 3?

x = 20.086

"Click here" to check the answer.

If e⁻² = 0.0135, what is x in the expression ln 0.0135= x?

x = −2

"Click here" to check the answer.

If ln 7.389 = 2, what is x in the expression e² = x?

x = 7.389

"Click here" to check the answer.

If ln 1 = 0, what is x in the expression e⁰ = x?

x = 1

"Click here" to check the answer.

If e = x, what is the value of x?

x = 1

"Click here" to check the answer.

The Calculator and the Natural Log (LN )

The key marked LN on the calculator is the natural logarithm key.

Example #1: Evaluate the expressions using a calculator.

Properties of common logarithms (log) apply to natural logarithms (ln) as well.

Example #2: Express 3 ln 5 as a single natural logarithm.

3 ln 5 = ln 5³	-Power property of logarithms
= ln 125	-Simplify

Example #3: Express ln 35 – ln 5 as a single natural logarithm.

ln 35 – ln 5 = ln	-Quotient property of logarithms
= ln 7	-Simplify

Example #4: Express 2 ln x + 3 ln y + ln 8 as a single natural logarithm.

2 ln x + 3 ln y + ln 8 =
ln x² + ln y³ + ln 8 =	-Power property of logarithms
ln 8x²y³	-Product property of logarithms

Stop! Go to Questions #1-8 about this section, then return to continue on to the next section.

Solving Equations with Natural Logarithms

Now let’s take a look at using the natural log to solve an equation.

Example #1: Solve 6.5^x = 44 for x.

ln 6.5^x= ln 44	-Take the natural log of both sides.
x ln 6.5 = ln 44	-Apply the Power property.
x =	-Divide both sides by ln 6.5.
x ≈ 2.02	-Round the answer to the nearest hundredth.

To check the above problem, substitute 2.02 in for x in the original equation.

6.5x = 44
6.5^2.02 ≈ 43.86	-Use the calculator to evaluate.

*Note: This problem can also be solved by taking the common logarithm (log) of both sides of the equation.

Natural logarithms (ln) must be used to solve problems that contain the number e.

Example #2: Solve e^x = 40 for x.

e^x = 40
ln e^x = ln 40	-Take the natural log of both sides.
x = ln 40	-Remember ln e^x = x.
x ≈ 3.69	-Use a calculator.

Example #3: Solve

+ 4 = 22 for x.

+ 4 = 22
= 18	-Subtract 4 from both sides.
ln = ln 18	-Take the natural log of both sides.
= ln 18	-Remember ln e^x = x, ∴ln = .
x = 3(ln 18)	-Multiply both sides by 3.
x ≈ 8.67	-Use a calculator.

Example #4: Solve 8e²^x−⁵ = 56 for x.

8e²^x−⁵ = 56
e²^x−⁵ = 7	-Divide both sides by 8.
ln e²^x−⁵ = ln 7	-Take the natural log of both sides.
2x − 5 = ln 7	-Remember ln e^x = x, ∴ln e²^x−⁵ = 2x − 5.
2x = ln 7 + 5	-Add 5 to both sides.
x =	-Divide by 2.
x ≈ 3.47	-Use a calculator.

Example #5: Solve 500 = 100e^0.75t for t.

500 = 100e^0.75t
5 = e^0.75t	-Divide both sides by 100.
ln 5 = ln e^0.75t	-Take the natural log of both sides.
ln 5 = 0.75t	-Remember ln e^x = x, ∴ln e^0.75t = 0.75t.
= t	-Divide both sides by 0.75.
t ≈ 2.1459	-Use a calculator.

Example #6: Solve ln (10x) = ln(3x + 14) for x.

ln (10x) = ln(3x + 14)
10x = 3x + 14	-Apply the One-to-one property.
7x = 14	-Subtract 3x from both sides.
x = 2	-Divide both sides by 2.

Example #7: Solve ln x + ln (x − 3) = ln 10 for x.

ln x + ln (x − 3) = ln 10
ln [x(x − 3)] = ln 10	-Apply the Product property.
x(x − 3) = 10	-Apply the One-to-one property.
x²− 3x = 10	-Distribute
x²− 3x − 10 = 0	-Subtract 10 from both sides, then apply the Zero product property to solve.
(x – 5)(x + 2) = 0	-Factor
x – 5 = 0 or x + 2 = 0	-Set both factors equal to zero.
x = 5 or x = −2	-Solve

Check both of these answers in the original problem. If either solution results in a negative logarithm, that solution must be denied.

Check:	for 5	for –2
	ln x + ln (x − 3) = ln 10	ln x + ln (x − 3) = ln 10
	ln 5 + ln (5 − 3) = ln 10	ln (–2) + ln (–2 − 3) = ln 10
	ln 5 + ln 2 = ln 10
	ln (–2) + ln (–5) = ln 10
	2.30 = 2.30
	*This equation yields two positive logarithms therefore 5 is a solution.	*This equation yields two negative logarithms therefore –2 cannot be a a solution because there are no negative logarithms.

Logarithmic and Exponential Equations

Stop! Go to Questions #9-14 about this section, then return to continue on to the next section.

Applications of Natural Logarithms

A formula using natural logarithms is the continuous compound interest formula where A is the final amount, P is the amount invested, r is the interest rate, and t is time.

Example #1: Find the value of $500 after 4 years invested at an annual rate of 9% compounded continuously.

A = unknown P = $500	r = 9% = 0.09 t = 4 years
A = Pe^rt
A = 500e^(0.09)(4)	-Substitute in P, r, and t.
A ≈ $716.66	-Evaluate and round to the nearest cent.

*On the calculator there is a feature for inputting e^x. That feature is found by pressing 2nd LN. Notice there is an e^x above the LN button. Press 500, then 2nd LN, then (0.09 × 4). Press enter and the answer appears!

Example #2: How long will it take to double your money if you deposit $500 at an annual rate of 7.2% compounded continuously?

Consider that the money deposited is $500, the initial amount. This amount doubled is $1000 and that will be the final amount to determine (A). Let t = the amount of time it will take to double the money.
A = Pe^rt
1000 = 500e^(0.072)t	-Substitute A = 1000, P = 500, r = 0.072
2 = e^(0.072)t	- Divide both sides by 500.
ln 2 = ln e^(0.072)t	-Take the natural log of both sides.
ln 2 = 0.072t	-Remember ln e^x = x, ∴ln e^(0.072)t = 0.072t.
= t	-Divide both sides by 0.072.
t ≈ 9.63	-Use the calculator to find the natural log of 2, then divide that answer by 0.072.

Stop! Go to Questions #15-30 to complete this unit.