SOLVING EQUATIONS AND APPLICATIONS |
 |
Unit Overview
In this unit, you will solve equations and justify the steps using properties of equality. You will apply linear equations to solve a variety of application problems.
Introduction to Solving Equations
 |
One of the most important properties in algebra is the distributive property. This property ties addition or subtraction together with multiplication. The distributive property allows you to write expressions in different forms and is given with the following definition.
 |
When variables represented in a table of values are linearly related and there is a constant difference in the x-values, there is also a constant difference in the y-values.
The Distributive Properties of Multiplication over Addition (01:26) An equation is like a balance scale. To keep both sides equal, any operation must be performed on each side.
| equation: a statement that has two expressions are equal 3x + 9 = 15 is an equation.variable: a symbol that represents an unknown value (generally a letter) The x in the example above is a variable. solution: any value of a variable that makes the equation true 2 is the solution to the example 3x + 9 = 15 terms: the components of an expression that are added or subtracted In “5 + 3x – x – 1”, each of these represents a term (5, 3x, x, 1). like terms: terms that contain the same variable with the same exponent 3x and x are considered like terms as well as 5 and 1. simplified: when all like terms have been combined and all parentheses have been removed In the expression 5 + 3x – x – 1, the simplified version is 4 + 2x. isolate the variable: rearrange and simplify an algebraic equation so that the variable that is being isolated is on one side of the equation and everything else is on the other side. |
To solve equations:
- Combine all like terms on each side (eliminate all parentheses by using the distributive property).
- Use opposite operations to isolate the variable.
- Justify the steps using the Properties of Equality.
Inverse Operations for Isolating Variables--Bowling (01:48)
Examples of Solving Equations: |
Use opposite operations to isolate the variable and justify the steps using the Properties of Equality.
 |
 |
To solve equations with fractions:
 |
| proportion: an equation that states two ratios are equal |
To solve proportions:
- Cross multiply.
- Solve by using opposite operations.
- Justify the steps using the Properties of Equality.
 |
Stop! Go to Questions #1-13 about this section, then return to continue on to the next section.
Direct Variation - A Special Case of a Linear Equation
This line is the graph of a direct variation because it passes through the origin.
 |
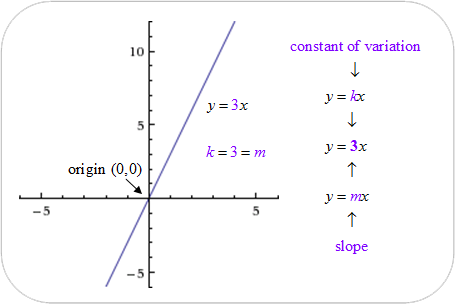There are many situations in which one quantity varies directly as another:
- An employee’s wages vary directly as the number of hours worked.
- The amount of sales tax varies directly as the total price of the merchandise.
- In y = kx, replace the x and y with the given values.
- Solve for k.
- Replace k in the direct variation equation, y = kx.
 |
Shortcuts for Solving Proportion Problems: Writing a Formula (03:30)  |
Using Proportions to Solve Direct-Variation Problems |
The general formula for direct variation is y = kx, where k represents the constant of variation.
  |
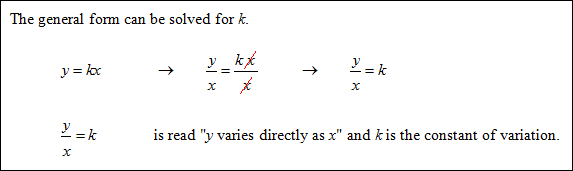Stop! Go to Questions #14-22 about this section, then return to continue on to the next section.
Using Equations to Solve Problems
Linear equations can be used to solve a variety of application problems.
Geometry |
| perimeter: distance around the outside of a figure. |
 |
Find the Average |
| average: total of all numbers, divided by how many numbers there are. |
 |
Business |
| revenue: the total amount of money received for goods cost: the amount of money associated with purchasing the goods to sell profit: the positive gain calculated by subtracting the cost from the revenue |
 |
Uniform Motion |
An object that moves at a constant rate is said to be in uniform motion.
Many uniform motion problems can be solved by using the formula d = rt, where d is the distance traveled, r is the rate of speed and t is the time.
 |
 |
Mixture Problem |
 |
Investment |
Simple interest problems can be solved by using the formula i = prt, where i is the interest, p is the principal, r is the interest rate, and t is the time.
 |
Work Problem |
 |
Formulas |
| formula: A formula is an equation that expresses relationship between two or more variables. |
Sometimes it is necessary to solve a formula for a specific variable. Solving for a variable in a formula involves similar steps to solving for a variable in an equation. To solve a formula for a specific variable, you must isolate the variable on one side of the equation.
For example, let's look at Ohm's Law:
  |
Stop! Go to Questions #23-32 to complete this unit.
