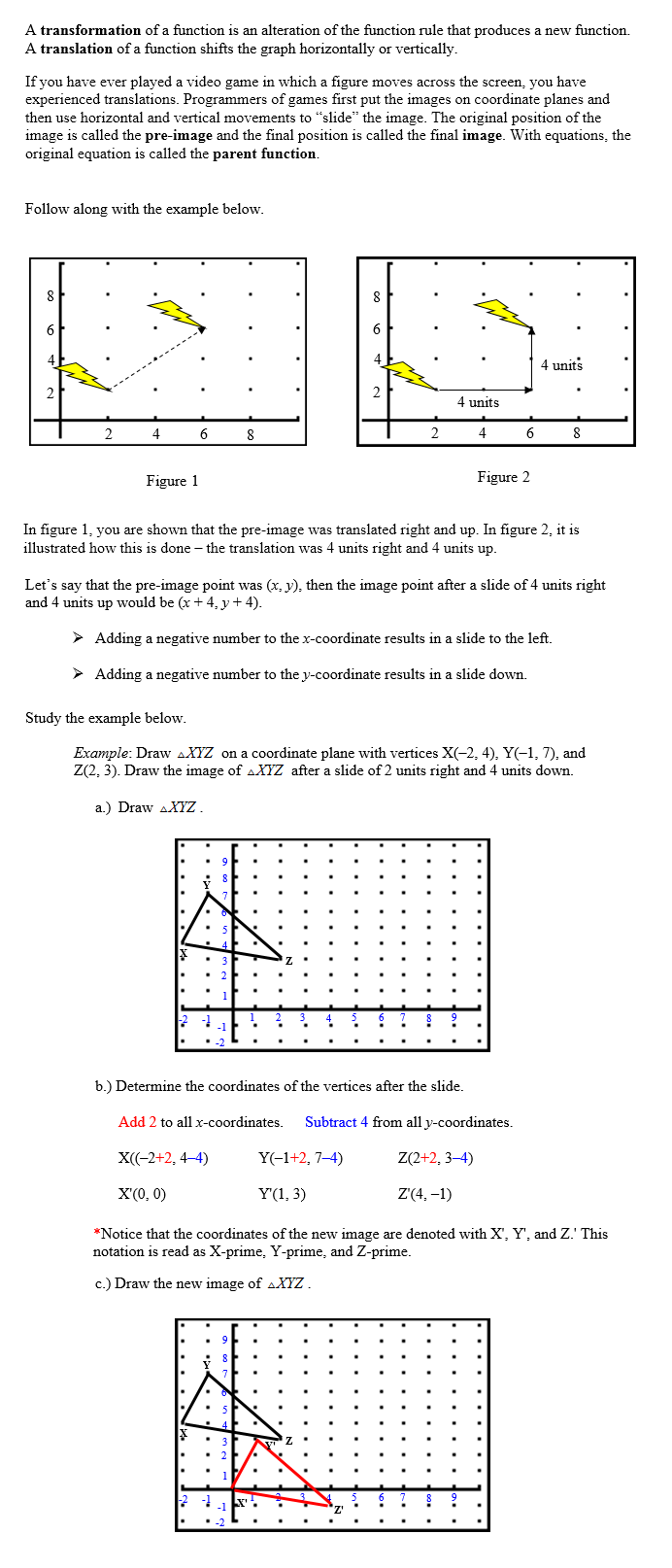
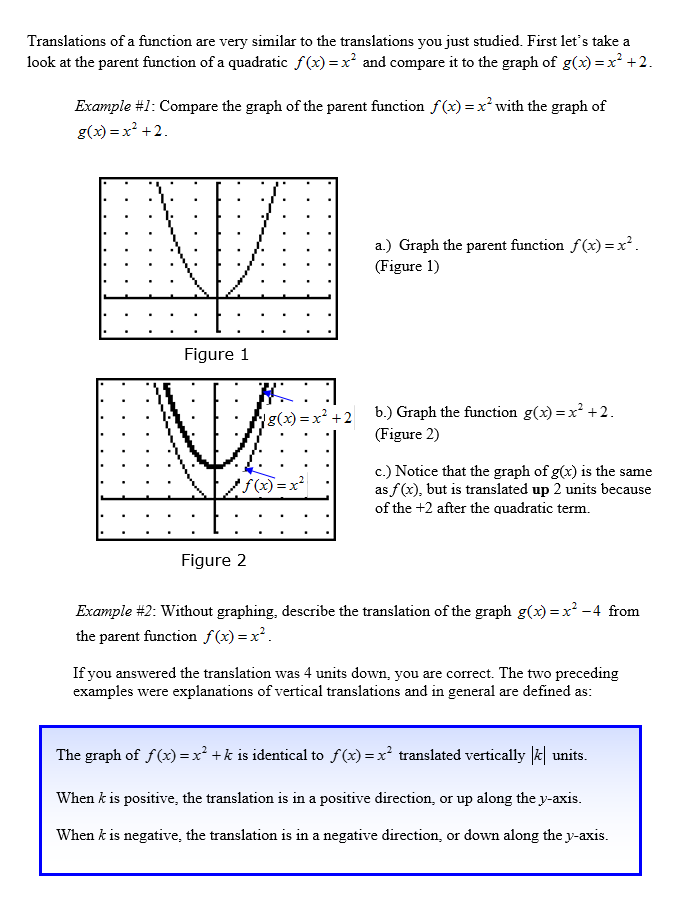
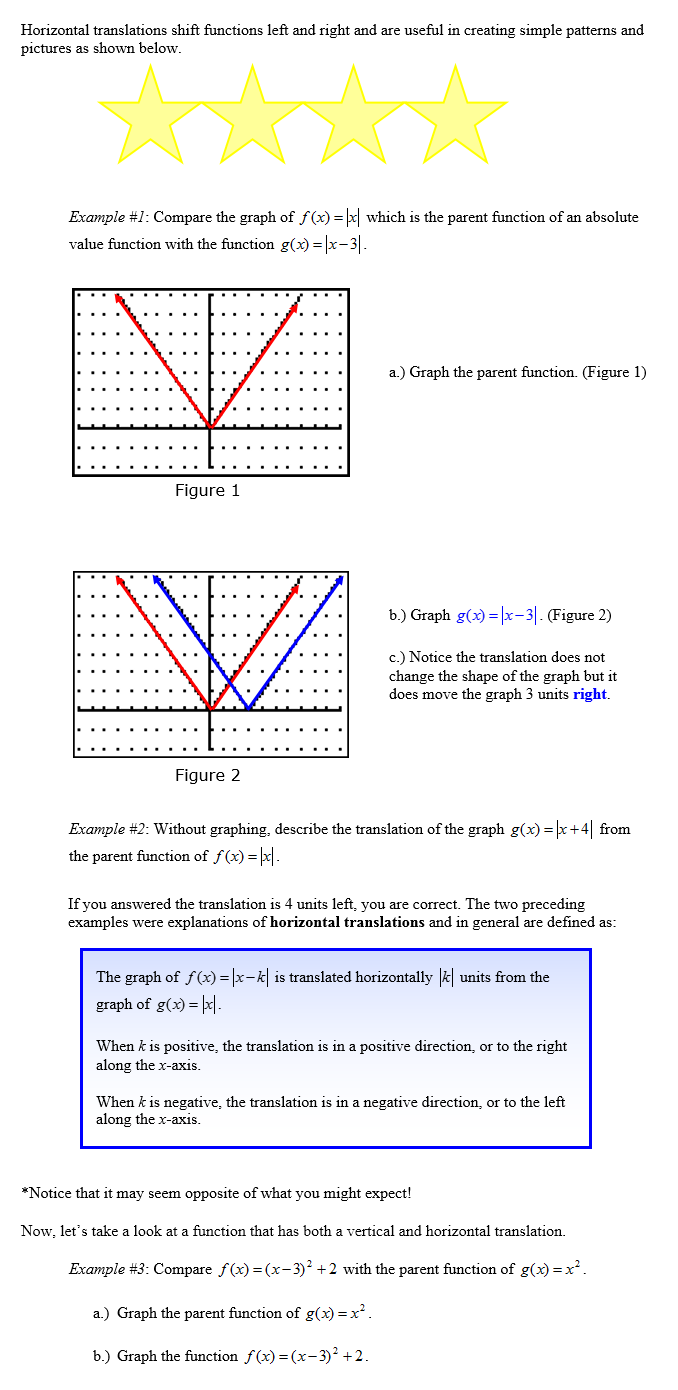
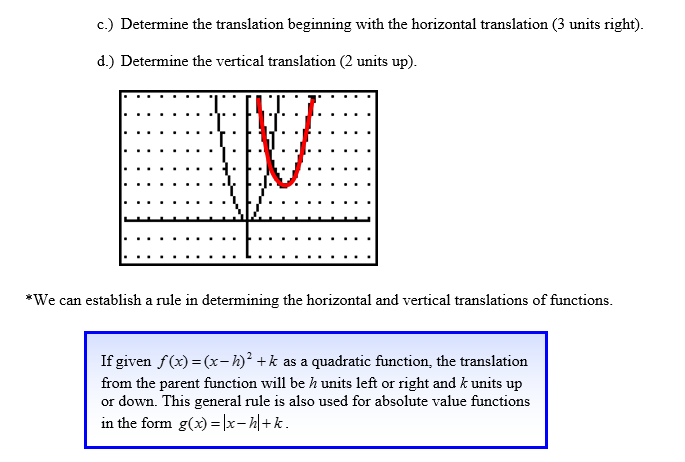
Vertical Stretches and Compressions

Try graphing these at: Math is Fun.
Type in y=x^2 for the blue equation and y=3x^2 for the red equation. The ^ symbol is found above the 6 key and denotes an exponent. You can also do this for the equations in example 4. After you have typed both in, the graphs appear. You should notice that the red graph is much steeper than the blue graph. We call this a stretch because the y values are higher for the same x-values. Now, under the red y, you will see a + and – button. Clicking these allows you to delete an equation or add additional equations. Click the + button. You should now see a green y= . You should now be able to input a 3rd equation. We are going to enter a new equation of y=(1/3) x2. How does the green graph compare to the others? Is it narrower? Wider? In case you are having trouble, click here to see the graphs.
You should notice that the green graph is wider. We call this a vertical compression because the y-values are smaller for the same x-values.
If you would like to see this using the activity we used earlier, go to Function Transformations - NLVM and make sure to click the forward arrow > as we did before until you reach "Multiplying by a Constant."
What happens if k is negative? What if we had –3 f (x)? Try it! Click the + button under the green y to add another function. Then type y = –3x^2.
You get a mirror image of 3 f (x). This is called a reflection about the x-axis. You still have a vertical stretch but in the opposite direction. |

|