MORE SYSTEMS OF EQUATIONS
 |
Unit Overview
In this unit you, will be introduced to another way of solving systems of equations using elimination. You will also learn about consistent, inconsistent, dependent, and independent systems. The unit will conclude with using systems to solve real world problems.
The Elimination Method
 |
Let's try an addition problem together. Solve the systems of equations using addition.
| 2x + y = 9 |
| 3x – y = 16 |
If we add to eliminate the y's, what equation will we then have?
5x = 25
"Click here" to check the answer.
What is the value of x?
x = 5
"Click here" to check the answer.
If we substitute the value of x in the first equation, what equation will we have?
2(5) + y = 9 or 10 + y = 9
"Click here" to check the answer.
What is the value of y?
y = –1
"Click here" to check the answer.
What is the ordered pair that solves this system of equation?
(5, –1)
"Click here" to check the answer.
How can the answer be checked in the first equation?
2(5) + –1 = 9
10 + –1 = 9
9 = 9
Checked!
"Click here" to check the answer.
How can the answer be checked in the second equation?
3(5) – (–1) = 16
15 + 1 = 16
16 = 16
Checked!
"Click here" to check the answer.
Solving Systems of Equations: Two Approaches (02:59) Elimination and the Addition Property of Equality (04:33)  |
Let's try a subtraction problem together. Solve the systems of equations using subtraction.
2x – 5y = –6 |
2x + y = 12 |
If we subtract to eliminate the x's, what equation will we then have?
Note: In subtraction, change the signs to their opposites, then add.
–6y = –18
"Click here" to check the answer.
What is the value of y?
y = 3
"Click here" to check the answer.
If we substitute the value of y in the first equation, what equation will we have?
2x + 3 = 12
"Click here" to check the answer.
What is the value of x?
x = 4.5
"Click here" to check the answer.
What is the ordered pair that solves this system of equation?
(4.5, 3)
"Click here" to check the answer.
How can the answer be checked in the first equation?
2(4.5) – 5(3) = –6
9 – 15 = –6
–6 = –6
Checked!
"Click here" to check the answer.
How can the answer be checked in the second equation?
2(4.5) + 3 = 12
9 + 3 = 12
12 = 12
Checked!
"Click here" to check the answer.
Using Subtraction and Division to Solve (02:51)  |
Elimination and the Multiplication Property of Equality (04:06)
 |
Let's try a problem together. Solve the systems of equations using elimination.
4x + 3y = –1 |
| 5x + 4y = 1 |
If we decide to eliminate y's, how will be make the coefficients the same?
Multiply the first equation by 4 and the second equation by 3.
4(4x + 3y = –1) and 3(5x + 4y = 1)
"Click here" to check the answer.
What equation will we use in place of the first equation?
16x + 12y = –4
"Click here" to check the answer.
What equation will we use in place of the second equation?
15x + 12y = 3
"Click here" to check the answer.
If we subtract to eliminate the y's, what is the value of x?
x = –7
"Click here" to check the answer.
If we substitute the value of x in the first equation, what equation will we have?
4(–7) + 3y = –1 or –28 + 3y = –1
"Click here" to check the answer.
What is the value of y?
y = 9
"Click here" to check the answer.
What is the ordered pair that solves this system of equation?
(–7, 9)
"Click here" to check the answer.
How can the answer be checked in the first equation?
4 (–7) + 3(9) = –1
–28 + 27 = –1
–1= –1
Checked!
"Click here" to check the answer.
How can the answer be checked in the second equation?
5(–7) + 4(9) = 1
–35 + 36 = 1
1 = 1
Checked!
"Click here" to check the answer.
Stop! Go to Questions #1-3 about this section, then return to continue on to the next section.
Choosing a Method for Solving Systems
When solving systems of linear equations using algebra, keep both methods in mind. Choose the method that works best for you.
 |
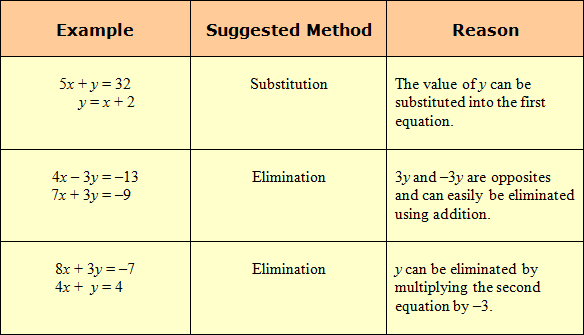Stop! Go to Questions #4-6 about this section, then return to continue on to the next section.
Consistent and Inconsistent Systems
 |
Let's check the solution by graphing both equations. Graph both equations in the previous example problem. Use a graphing calculator or graph on paper. Also, click here to navigate to an online grapher.
Is the point of intersection the same as the solution above?
Yes, (–1, 0)
"Click here" to check the answer.
Check to see if both equations are graphed correctly.
"Click here" to check the graph.
 |
Let's check the solution by graphing both equations. Graph both equations in the previous example problem. Use a graphing calculator or graph on paper. Also, click here to navigate to an online grapher.
What is true about the graphs of the two equations?
The lines are parallel.
"Click here" to check the answer.
When solving systems of equations algebraically,
how will we know when the lines are parallel?
The variables will drop out and the final statement will be false.
"Click here" to check the answer.
Check to see if both equations are graphed correctly.
"Click here" to check the graph.
 |
Let's check the solution by graphing both equations. Graph both equations in the previous example problem. Use a graphing calculator or graph on paper. Also, click here to navigate to an online grapher.
What is true about the graphs of the two equations?
The graphs of the lines are the same line.
"Click here" to check the answer.
When solving systems of equations algebraically, how can it be
determined that there are an infinite number of solutions to the system?
The variables will drop out and the final statement be 0 = 0.
"Click here" to check the answer.
Check to see if both equations are graphed correctly.
"Click here" to check the graph.
Stop! Go to Questions #7-12 about this section, then return to continue on to the next section.
Independent and Dependent Systems
 |
Stop! Go to Questions #13-17 about this section, then return to continue on to the next section.
Applications of Systems of Equations
 |
Practical Problem: Pizza! (03:46)Stop! Go to Questions #18-33 to complete this unit.
