LINEAR EQUATIONS AND GRAPHS
 |
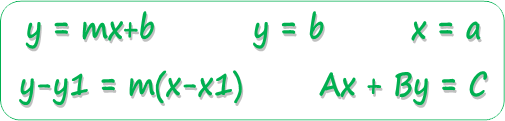Unit Overview
This unit is about linear equations and their graphs. In this unit, you will learn how to write equations of lines using the slope‑intercept form of a line and the point‑slope form. You will investigate transformations of the parent function, y = x, and learn how to graph linear equations in standard form using the x- and y-intercepts. You will take a closer look at horizontal and vertical lines. The unit will conclude with a discussion of the equations and graphs of parallel lines and perpendicular lines.
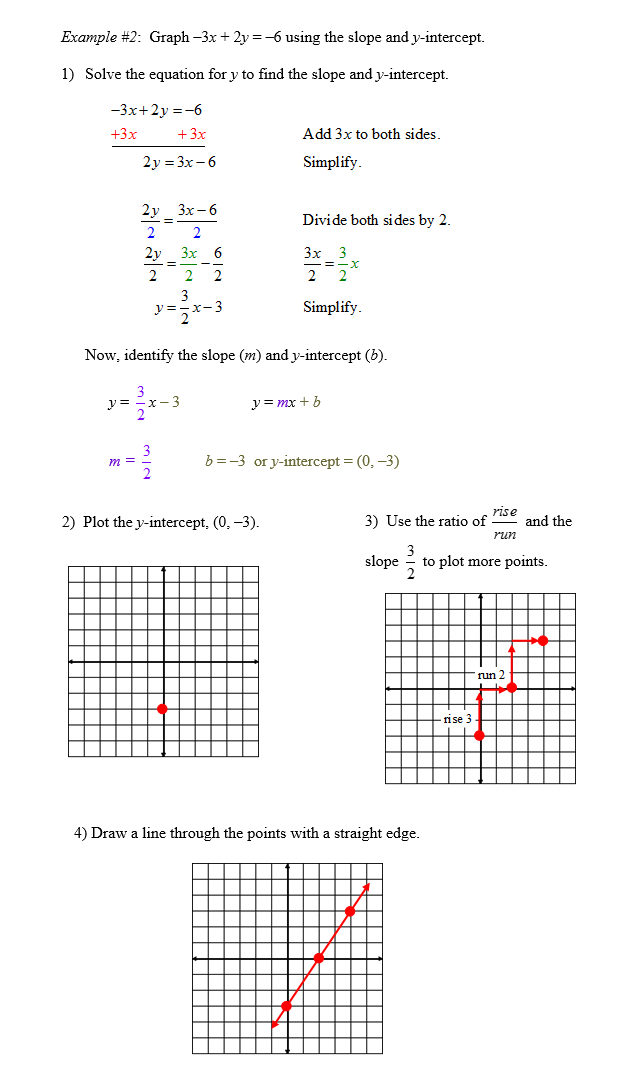
Slope-Intercept Form
 |
 |
|
 |
Stop! Go to Questions #1-6 about this section, then return to continue on to the next section.
Parent Functions and Transformations
 |
Use a graphing calculator or knowledge from above to answer the below questions. Also, there is a graphing program online at Desmos | Graphing Calculator.
 |
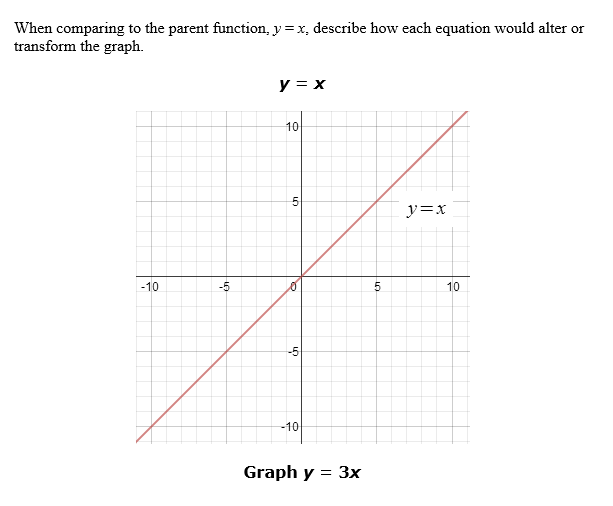Describe the translation for y = 3x from the parent function y = x.
The steepness of the line (slope) will change from m = 1 (1/1) to m = 3 (3/1).
"Click here" to check the answer.
How does the y-intercept change?
The y-intercept remains 0. The graph passes through (0, 0).
"Click here" to check the answer.
View the graphs.
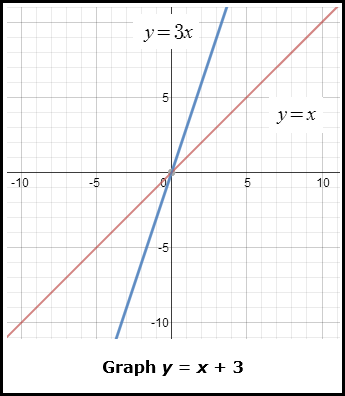
"Click here" to view both graphs.
Describe the translation for y = x + 3 from the parent function y = x.
The graph is translated 3 units up and passes through the y-axis at (0, 3).
"Click here" to check the answer.
How does the slope change?
The slope (m = 1) remains the same (rise / run = 1 / 1).
"Click here" to check the answer.
How does the y-intercept change?
The y-intercept changes from (0, 0) to (0, 3).
"Click here" to check the answer.
View the graphs.
Describe the translation for y = –x from the parent function y = x.
The slope of the line is now negative and goes through Quadrants II and IV.
"Click here" to check the answer.
Describe one way to count out the slope (rise / run) of the graph.
The rise over run is down 1, then right one.
"Click here" to check the answer.
Describe a second way to count out the slope (rise / run) of the graph.
The rise over run is up 1, then left 1.
"Click here" to check the answer.
How does the y-intercept change?
The y-intercept remains 0. The graph passes through (0, 0).
"Click here" to check the answer.
View the graphs.
Describe the translation for y = 2x – 5 from the parent function y = x.
The graph is translated 5 units down and the slope becomes steeper.
"Click here" to check the answer.
How does the slope change?
The steepness of the line (slope) changes from m = 1 (1/1) to m = 2 (2/1).
"Click here" to check the answer.
How does the y-intercept change?
The y-intercept changes from (0, 0) to (0, –5).
"Click here" to check the answer.
View the graphs.
 |
Stop! Go to Questions #7-10 about this section, then return to continue on to the next section.
Graphing a Line Using the x- and y-intercepts
 |
|
|
Stop! Go to Questions #11-15 about this section, then return to continue on to the next section.
Point-Slope Form
|
What would the equation look like in standard form?
–x + y = –1
"Click here" to check the answer.
The equation could be transformed into an equivalent equation in simpler form by multiplying both sides by –1. What would that equation look like?
x – y = 1
"Click here" to check the answer.
|
Stop! Go to Questions #16-20 about this section, then return to continue on to the next section.
Equations of Horizontal and Vertical Lines
 |
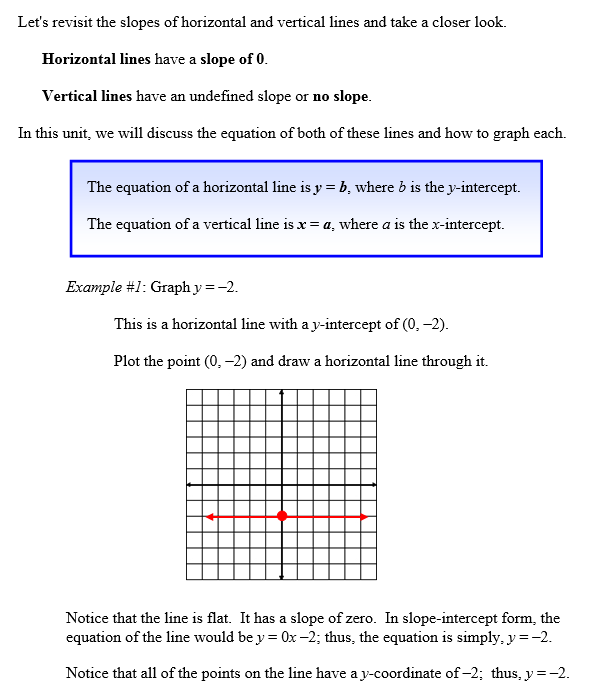What are the coordinates of a few points on this line?
Sample Answer: (0, –2), (–5, –2), (3, –2), (100, –2)
"Click here" to check the answer.
 |
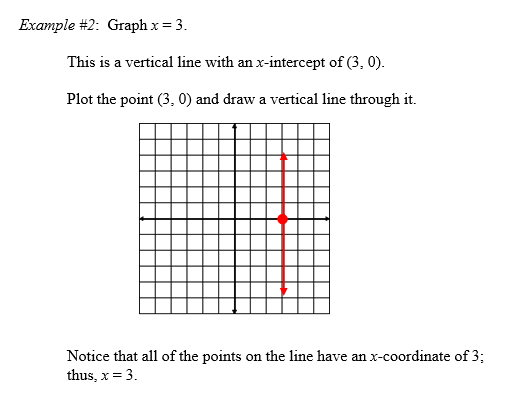What are the coordinates of a few points on this line?
Sample Answer: (3, 0), (3, –4), (3, 10), (3, –1000)
"Click here" to check the answer.
Stop! Go to Questions #21-25 about this section, then return to continue on to the next section.
Parallel and Perpendicular Lines
 |
Stop! Go to Questions #26-32 to complete this unit.
