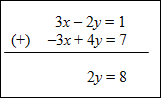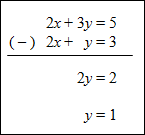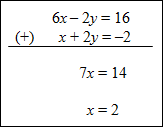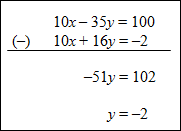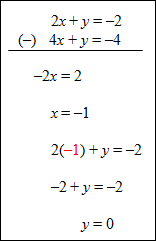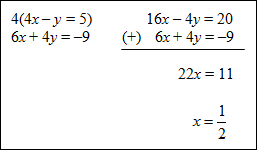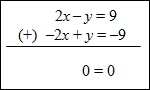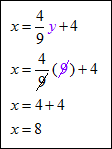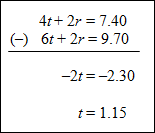More Systems of Equations

PDF

MORE SYSTEMS OF EQUATIONS

Unit Overview
In this unit you, will be introduced to another way of solving systems of equations using elimination. You will also learn about consistent, inconsistent, dependent, and independent systems. The unit will conclude with using systems to solve real world problems.

The Elimination Method

Another way to algebraically solve a system of equations is by eliminating a variable. This process involves adding or subtracting the equations, depending on whether the terms are opposites (then add) or the same (then subtract).

First put both equations into standard form (Ax + By = C)

Elimination Using Addition

Example #1: Solve the system shown below using the elimination method.

3x – 2y = 1

–3x + 4y = 7

Step 1: Think: Are any terms that are the same or opposites?

Yes! In this case, the 3x and –3x are opposites.

Step 2: Use the addition property of equality to combine the two equations into one.

Step 3: Solve the resulting equation for y and substitute this value into one of the original equations for y, and then solve for x.

2y = 8

y = 4

3x – 2y = 1

3x – 2(4) = 1

3x – 8 = 1

3x = 9

x = 3

The solution to this system of equations is (3, 4).

Let's try an addition problem together. Solve the systems of equations using addition.

2x + y = 9

3x – y = 16

If we add to eliminate the y's, what equation will we then have?

5x = 25

"Click here" to check the answer.

What is the value of x?

x = 5

"Click here" to check the answer.

If we substitute the value of x in the first equation, what equation will we have?

2(5) + y = 9 or 10 + y = 9

"Click here" to check the answer.

What is the value of y?

y = –1

"Click here" to check the answer.

What is the ordered pair that solves this system of equation?

(5, –1)

"Click here" to check the answer.

How can the answer be checked in the first equation?

2(5) + –1 = 9
10 + –1 = 9
9 = 9
Checked!

"Click here" to check the answer.

How can the answer be checked in the second equation?

3(5) – (–1) = 16
15 + 1 = 16
16 = 16
Checked!

"Click here" to check the answer.

Solving Systems of Equations: Two Approaches (02:59)

Elimination and the Addition Property of Equality (04:33)

Elimination Using Subtraction

Example #2: Solve the system shown below using the elimination method.

2x + 3y = 5

2x + y = 3

Step 1: In this example, the x terms are the same. To eliminate the x’s, subtract the two equations to combine them into one.

Step 2: Substitute 1 for y into either of the original equations, and then solve for x.

2x + 3y = 5

2x + 3(1) = 5

2x + 3 = 5

2x = 2

x = 1

The solution to this system of equations is (1, 1).

Let's try a subtraction problem together. Solve the systems of equations using subtraction.

2x – 5y = –6

2x + y = 12

If we subtract to eliminate the x's, what equation will we then have?

Note: In subtraction, change the signs to their opposites, then add.

–6y = –18

"Click here" to check the answer.

What is the value of y?

y = 3

"Click here" to check the answer.

If we substitute the value of y in the first equation, what equation will we have?

2x + 3 = 12

"Click here" to check the answer.

What is the value of x?

x = 4.5

"Click here" to check the answer.

What is the ordered pair that solves this system of equation?

(4.5, 3)

"Click here" to check the answer.

How can the answer be checked in the first equation?

2(4.5) – 5(3) = –6
9 – 15 = –6
–6 = –6
Checked!

"Click here" to check the answer.

How can the answer be checked in the second equation?

2(4.5) + 3 = 12
9 + 3 = 12
12 = 12
Checked!

"Click here" to check the answer.

Using Subtraction and Division to Solve (02:51)

Elimination Using Multiplication and Addition or Subtraction

Example #3: Solve the system shown below using the elimination method.

3x – y = 8

x + 2y = –2

Step 1: Multiply the first equation by 2 to produce opposites for y.

2(3x – y = 8)	6x – 2y = 16
x + 2y = –2	x + 2y = –2

Step 2: Add the two equations to eliminate y.

Step 3: Substitute 2 for x in either of the original equations, and then solve for y.

3x – y = 8

3(2) – y = 8

6 – y = 8

–y = 2

y = –2

The solution to this system of equations is (2, –2).

Elimination and the Multiplication Property of Equality (04:06)

Example #4: Solve the system shown below using the elimination method.

2x – 7y = 20

5x + 8y = –1

Step 1: Multiply the first equation by 5 and the second equation by 2 to produce the same coefficient on the x term.

5(2x – 7y = 20)	10x – 35y = 100
2(5x + 8y = –1)	10x + 16y = –2

Step 2: Subtract the two new equations to eliminate x.

Step 3: Substitute –2 for y in either of the original equations.

2x – 7y = 20

2x – 7(–2) = 20

2x + 14 = 20

2x = 6

x = 3

The solution to this system of equations (3, –2).

Let's try a problem together. Solve the systems of equations using elimination.

4x + 3y = –1

5x + 4y = 1

If we decide to eliminate y's, how will be make the coefficients the same?

Multiply the first equation by 4 and the second equation by 3.
4(4x + 3y = –1) and 3(5x + 4y = 1)

"Click here" to check the answer.

What equation will we use in place of the first equation?

16x + 12y = –4

"Click here" to check the answer.

What equation will we use in place of the second equation?

15x + 12y = 3

"Click here" to check the answer.

If we subtract to eliminate the y's, what is the value of x?

x = –7

"Click here" to check the answer.

If we substitute the value of x in the first equation, what equation will we have?

4(–7) + 3y = –1 or –28 + 3y = –1

"Click here" to check the answer.

What is the value of y?

y = 9

"Click here" to check the answer.

What is the ordered pair that solves this system of equation?

(–7, 9)

"Click here" to check the answer.

How can the answer be checked in the first equation?

4 (–7) + 3(9) = –1
–28 + 27 = –1
–1= –1
Checked!

"Click here" to check the answer.

How can the answer be checked in the second equation?

5(–7) + 4(9) = 1
–35 + 36 = 1
1 = 1
Checked!

"Click here" to check the answer.

Stop! Go to Questions #1-5 about this section, then return to continue on to the next section.

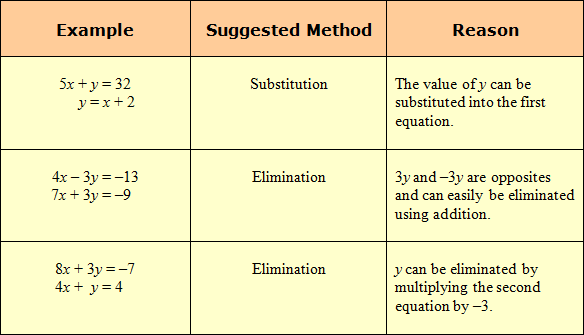
Choosing a Method for Solving Systems

When solving systems of linear equations using algebra, keep both methods in mind. Choose the method that works best for you.

Stop! Go to Questions #6-8 about this section, then return to continue on to the next section.

Consistent and Inconsistent Systems

In the previous unit, you learned that a system of equations may have a unique solution (one ordered pair (x, y)), many solutions, or no solution. In this unit, we are going to expand on this and say that if a system has one or many solutions, the system is called consistent. If a system has no solution, it is inconsistent.

To determine if a system is consistent or inconsistent, you need to solve it algebraically, either by substitution or elimination, or graphically. For our purposes, we will solve all systems algebraically.

Example #1: Solve the system of equations shown below.

2x + y = –2

4x + y = –4

Step 1: Solve the system algebraically by subtracting the systems.

The solution is (–1, 0), so the system has one unique solution and is consistent.

Let's check the solution by graphing both equations. Graph both equations in the previous example problem. Use a graphing calculator or graph on paper. Also, click here to navigate to an online grapher.

Is the point of intersection the same as the solution above?

Yes, (–1, 0)

"Click here" to check the answer.

Check to see if both equations are graphed correctly.

"Click here" to check the graph.

Example #2: Solve the system of equations shown below.

4x – y = 6

y – 4x = 4

Step 1: Solve the system by using substitution. Solve the second equation for y and substitute this value into the first equation.

y = 4 + 4x

4x – (4 + 4x) = 6

4x – 4 – 4x = 6

–4 ≠ 6

Since –4 does not equal 6, there is no ordered pair that satisfies the system; therefore, the system is inconsistent.

What is true about the graphs of the two equations?

The lines are parallel.

"Click here" to check the answer.

When solving systems of equations algebraically,
how will we know when the lines are parallel?

The variables will drop out and the final statement will be false.

"Click here" to check the answer.

Check to see if both equations are graphed correctly.

"Click here" to check the graph.

Example #3: Solve the system of equations shown below.

6x – 2y = –4

y = 3x +2

Step 1: Solve the system by using substitution. Substitute the value for y into the first equation to solve for x.

6x – 2(3x +2) = –4

6x – 6x – 4 = –4

–4 = –4

0 = 0

Since 0 = 0 for any value of x, the system of equations has infinite solutions. Every ordered pair (x, y) satisfies both equations. The system is consistent (and dependent which is discussed in the next section). The two equations describe the same line.

What is true about the graphs of the two equations?

The graphs of the lines are the same line.

"Click here" to check the answer.

When solving systems of equations algebraically, how can it be
determined that there are an infinite number of solutions to the system?

The variables will drop out and the final statement be 0 = 0.

"Click here" to check the answer.

Check to see if both equations are graphed correctly.

"Click here" to check the graph.

Stop! Go to Questions #9-14 about this section, then return to continue on to the next section.

Independent and Dependent Systems

The consistent systems that you just learned about can be categorized as independent or dependent.

If one unique ordered pair (x, y) satisfies both equations, then the system is an independent system (one solution).

If every ordered pair is a solution of both equations, then the system is a dependent system (many solutions).

To determine if a system is independent or dependent, solve the system algebraically or graphically.

Example #1: Solve the system of equations shown below.

4x – y = 5

6x + 4y = –9

Step 1: Multiply the first equation by 4 so the “y” values are opposites, and then add the two equations.

Step 2: Substitute

for x in either of the original equations and solve for y.

4x – y = 5

– y = 5

2 – y = 5

–y = 3

y = –3

The solution is (

, –3). Since the system has one solution, this means the system is independent.

Example #2: Solve the system of equations shown below.

2x – y = 9

–2x + y = –9

Step 1: Add the two equations together to eliminate x or y.

Since this solution produces a true statement that 0 = 0, the solution has many solutions and this means that the system is dependent.

Example #3: Solve the system of equations shown below.

x + y = 12

x = y + 4

Step 1: Use substitution.

Step 2: Substitute 9 for y in either of the original equations and solve for x.

The solution is (8, 9). Since the system has one solution, this means the system is independent.

Summary for the Types of Systems of Equations

The solution to a system of equations can be described as follows.

Inconsistent Systems will have no solution. The lines of the equations are parallel.

Consistent Systems will have one or an infinite number of solutions

Independent consistent systems have one solution. The lines intersection at one point.

Dependent Consistent Systems have many solutions. The lines are the same line and coincide at all points.

Stop! Go to Questions #15-21 about this section, then return to continue on to the next section.

Applications of Systems of Equations

Systems of equations can be used for many real-world problems when more than one variable is unknown. The following examples demonstrate this process.

Example #1: The Jets scored 4 more points than the Vets. The total of their scores was 38. How many points did each team score?

Step 1: Define a variable for each unknown.

j = Jet’s score

v = Vet’s score

Step 2: Determine what is known and represent this information using equations.

We know the Jets scored 4 more than the Vets so,

j = v + 4

We also know that their combined score was 38 so,

j + v = 38

Step 3: Use the two equations just found to determine each team score by using substitution or elimination.

j = v + 4

j + v = 38

Since you know the value of j, j = v + 4, substitute this into the second equation for j and solve for v.

(v + 4) + v = 38

2v + 4 = 38

2v = 34

v = 17

The Vets scored 17 points.

Use this information to substitute v in either of the original equations to determine the number of points the Jets scored.

j = 17 + 4

j = 21

The Jets scored 21 points.

The answer to the problem is the Vets scored 17 points and the Jets scored 21 points..

Example #2: Four cans of tuna and 2 boxes of rice cost $7.40. Six cans of tuna and 2 boxes of rice cost $9.70. Find the cost of each item.

Step 1: Define a variable for each unknown.

t = one can of tuna

r = one box of rice

Step 2: Use the given information to write the equations for the system..

Since we know 4 cans of tuna and 2 boxes of rice cost $7.40, the equation would be:

4t + 2r = 7.4

We also know that 6 cans of tuna and 2 boxes of rice cost $9.70. The equation would be:

6t + 2r = 9.70

Our two equations would be:

4t + 2r = 7.40

6t + 2r = 9.70

Step 3: Use elimination with subtraction to eliminate r.

This tells us that each can of tuna costs $1.15.

Step 4: Now substitute this value back into one of the original equations to find out how much each box of rice costs.

4(1.15) + 2r = 7.40

4.60 + 2r = 7.40

2r = 2.80

r = 1.40

Each box or rice costs $1.40.

Practical Problem: Pizza! (03:46)

Stop! Go to Questions #22-40 to complete this unit.

Below are additional educational resources and activities for this unit.

Solving Systems of Equations

Solving Systems of Equations by Elimination