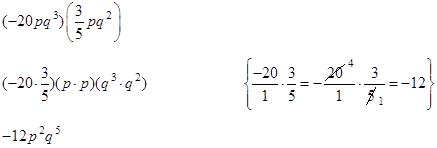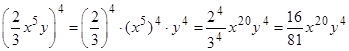LAW OF EXPONENTS
|
Unit Overview
In a previous unit, you were introduced to properties of exponents. In this unit, you will expand on the concept of exponent properties which are rules used for simplifying algebraic expressions. It is important to understand these rules as exponents are used in real-world situations such as finding area and volume. In biology and physics you may encounter quotients that involve exponents.
Multiplying Monomials
In the expression, 3100, three is a product of itself 100 times. The number 3 represents the base and the 100 represents the exponent. The exponent tells how many times the base is used as a factor.
| Example #1: 54 = 5 ⋅ 5 ⋅ 5 ⋅ 5 |
| = 25 ⋅ 5 ⋅ 5 |
| = 125 ⋅ 5 |
| = 625 |
| Example #2: 33 = 3 ⋅ 3 ⋅ 3 |
| = 9 ⋅ 3 |
| = 27 |
 |
The property above states that if you are multiplying like bases (in the case above “a”), then to simplify you will add the exponents.
| Example #3: 23 ⋅ 24 = 23+4= 27 |
To prove this example, we will expand each term, count the bases and rewrite the term using one base and one exponent.
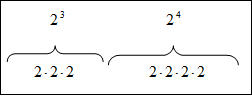 -count the number of bases and use this as your exponent 27 *This is the same answer we found when we used the product of powers rule. |
The product of powers rule can be used to find the product of monomials. A monomial is an algebraic expression that is a constant (number), a variable, or a product of a constant and one or more variables. The constant (or numerical factor) is called the coefficient.
Examples of monomials: 3, m, –5xy
To simplify a product of monomials:
| 1) Multiply the coefficients. | |||||||||||||||||
2) Use the product of powers rule to simplify the variables.
|
|||||||||||||||||
.
Now try one:
Simplify (34a2b3)(3–3a5b–3).
3a7
Note: b0 is one and b should not be in your answer.
"Click here" to check the answer.
Stop! Go to Questions #1-9 about this section, then return to continue on to the next section.
Geometry Connection
The volume (V) of a right rectangular prism can be found using the formula V = lwh, where l = length, w = width, and h = height. Find the volume of the following prism.
 |
Find the volume when l = 7x w = 8xy and h = 2xy.
V = 112x3y2
"Click here" to check the answer.
Stop! Go to Questions #10-12 about this section, then return to continue on to the next section.
Powers and Products
Sometimes in algebra it is necessary to raise a power to a power as in the example (x3)2. In this case, you would use the exponent rule called “Power of a Power” Rule.
 |
As you can see by the rule stated above, if you have a power raised to another power, then you multiply the exponents.
| Example #1: Simplify (32)4. | |
|
| Example #2: Simplify (m3)5. | |
|
| Example #3: Simplify (yn)3. | |
|
Another property of exponents is used for any number of factors inside parentheses. This rule or property is called Power-of-a-Product.
 |
Notice that in this property the exponent is taken to each factor. Let’s try a few examples using this property.
| Example #4: Simplify (2x)3. | |
|
| Example #5: Simplify (5yz)2. | |
|
The last two properties, Power-of-a-Power, and Powers-of-a-Product, can be used together as shown in the examples below.
| Example #6: Simplify (x3y2)4. | |
|
| Example #7: Simplify (3n2m4)3. | |
|
Example #8: Simplify  . |
|
|
Use multiple rules to simplify this expression (2a3)3 ⋅ (3a2b4).
24a11b4
"Click here" to check the answer.
Integer Exponents (01:34)Stop! Go to Questions #13-19 about this section, then return to continue on to the next section.
Powers of (–1)
Recall that when multiplying two negative numbers, the result will be a positive answer. What will the answer be when you multiply three negative numbers? four negative numbers? and so on. Let’s take a look at what happens with negative numbers to odd and even powers by using a base of –1.
| (–1)2 = (–1)(–1) = +1 |
| (–1)3 = (–1)(–1)(–1) = –1 |
| (–1)4 = (–1)(–1)(–1)(–1) = +1 |
| (–1)5 = (–1)(–1)(–1)(–1)(–1) = –1 |
| (–1)6 = ? (–1)7 = ? |
What do you suppose the result of (–1)6 will be? What about (–1)7 ?
If you answered +1 for (–1)6 and –1 for (–1)7, you are correct.
From this, we can conclude:
Even powers of a negative base will result in a positive answer. |
Odd powers of a negative base will result in a negative answer. |
| Example #1: Simplify (–4y)3. | |
|
| Example #2: Simplify (–m)100. | |
|
Stop! Go to Questions #20-40 to complete this unit.
