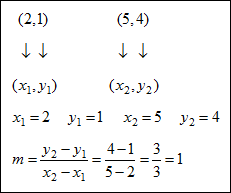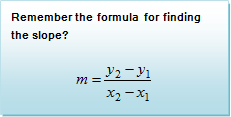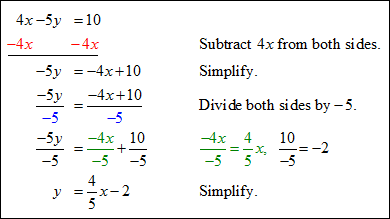LINEAR EQUATIONS AND GRAPHS


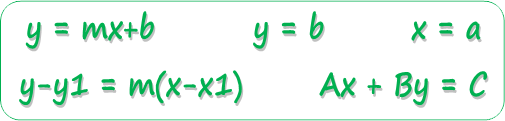Unit Overview
This unit is about linear equations and their graphs.  In this unit, you will learn how to write equations of lines using the slope‑intercept form of a line and the point‑slope form.  You will investigate transformations of the parent function, y = x, and learn how to graph linear equations in standard form using the x- and y-intercepts.  You will take a closer look at horizontal and vertical lines.  The unit will conclude with a discussion of the equations and graphs of parallel lines and perpendicular lines.


Slope-Intercept Form

One way of graphing the equation of a line is by using the slope-intercept form which identifies the slope and the y-intercept.




Example #1:  Identify the slope and y-intercept for the equation y = x – 4.

Identify the slope (m) and y-intercept (b).
 
y = x – 4           y = mx + b
 
m =           b = –4  or y-intercept = (0, –4)

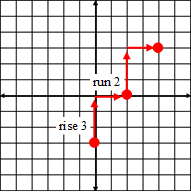
To graph a line using the slope and y-intercept:

1)  Arrange the equation into the form y = mx + b.  (This means to solve the equation for y.)
 
2)  Identify the y-intercept and plot the point (0, b).
 
3)  Use the ratio for slope to plot more points.
 
4)  Draw a line through the points with a straight edge.



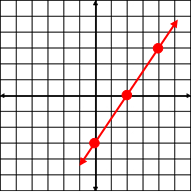
Example #2:  Graph –3x + 2y = –6 using the slope and y-intercept.

1)  Solve the equation for y to find the slope and y-intercept.


    Now, identify the slope (m) and y-intercept (b).

y = x – 3           y = mx + b
 
m =           b = –3  or y-intercept = (0, –3)

2)  Plot the y-intercept, (0, –3).
3)  Use the ratio of and the
slope to plot more points.

 
4)  Draw a line through the points with a straight edge. 




Stop!  Go to Questions #1-6 about this section, then return to continue on to the next section.


Parent Functions and Transformations


Transformation is when the parent function is changed by either adding, subtracting, multiplying, or dividing the original function by a constant (number). 

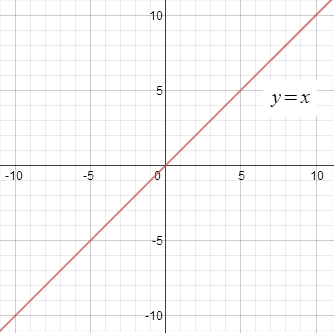
  • Multiplying will change the slope or the steepness of the line.
  • Adding or subtracting will move the line in the direction of up, down, left or right which is called  a translation. 

Let’s explore what happens to the parent function as we change the values of m and b in the linear function y = mx + b.

Use a graphing calculator or knowledge from above to answer the below questions.  Also, there is a graphing program online at https://www.desmos.com/calculator.

When comparing to the parent function, y = x, describe how each equation would alter or transform the graph.

y = x
Graph y = 3x

question1Describe the translation for y = 3x from the parent function y = x.

The steepness of the line (slope) will change from m = 1 (1/1) to m = 3 (3/1).

"Click here" to check the answer.




question1How does the y-intercept change?

The y-intercept remains 0. The graph passes through (0, 0).

"Click here" to check the answer.



question1View the graphs.

"Click here" to view both graphs.


question1Describe the translation for y = x + 3 from the parent function y = x.

The graph is translated 3 units up and passes through the y-axis at (0, 3).

"Click here" to check the answer.




question1How does the slope change?

The slope (m = 1) remains the same (rise / run = 1 / 1).

"Click here" to check the answer.




question1How does the y-intercept change?

The y-intercept changes from (0, 0) to (0, 3).

"Click here" to check the answer.




question1View the graphs.

"Click here" to view both graphs.


question1Describe the translation for y = –x from the parent function y = x.

The slope of the line is now negative and goes through Quadrants II and IV.

"Click here" to check the answer.



question1Describe one way to count out the slope (rise / run) of the graph.

The rise over run is down 1, then right one.

"Click here" to check the answer.



question1Describe a second way to count out the slope (rise / run) of the graph.

The rise over run is up 1, then left 1.

"Click here" to check the answer.



question1How does the y-intercept change?

The y-intercept remains 0. The graph passes through (0, 0).

"Click here" to check the answer.




question1View the graphs.

"Click here" to view both graphs.

 

question1Describe the translation for y = 2x – 5 from the parent function y = x.

The graph is translated 5 units down and the slope becomes steeper.

"Click here" to check the answer.




question1How does the slope change?

The steepness of the line (slope) changes from m = 1 (1/1) to m = 2 (2/1).

"Click here" to check the answer.




question1How does the y-intercept change?

The y-intercept changes from (0, 0) to (0, –5).

"Click here" to check the answer.




question1View the graphs.

"Click here" to view both graphs.


To sum it up, when the parent function was multiplied by 3, the slope (steepness of the line) was greater and when it was multiplied by –1, the slope of the line became a decreasing line instead of an increasing line, from left to right.  In both instances, the y‑intercept remained the same.

When 3 was added to the parent function, the linear graph moved up 3 units, but the slope remained the same.

Finally, in the last example, the graph was both multiplied by 2 and five was subtracted.  Thus, the slope (steepness of the line) was greater, and the graph moved down 5 units.

Stop!  Go to Questions #7-11 about this section, then return to continue on to the next section.


Graphing a Line Using the x- and y-intercepts

Another way to graph a line is by plotting the x- and y-intercepts.  To graph using this method, it is recommended that the linear equation be expressed in standard form first.   


To find the x- and y-intercepts:

1)  Replace x with 0 in the equation and solve for y to locate the y‑intercept (0, y).
 
2)  Replace y with 0 in the equation and solve for x to locate the x‑intercept (x, 0).
 
3)  Plot the two points and draw a straight line through them using a straight edge (ruler or something similar).



Example #1:  Graph 2x – 3y = 6 by using the x- and y-intercepts.

Solve for the y-intercept (let x = 0).

Solve for the x-intercept (let y = 0).
   
1)  2(0) – 3y = 6         

2)  2x – 3(0) = 6
              –3y = 6                 2x = 6
                  y = –2                    x = 3
y-intercept = (0, –2) x-intercept = (3, 0)


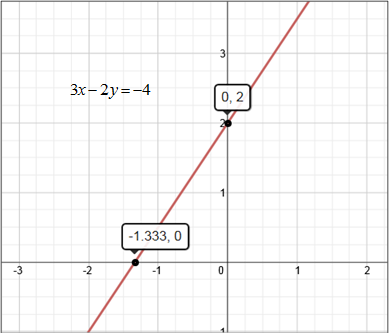
Example #2:  Graph 3x = 2y – 4 by using the x- and y-intercepts.

First put the equation into standard form (Ax + By = C).
 

Solve for the y-intercept (let x = 0).

Solve for the x-intercept (let y = 0).
1)  3(0) – 2y = –4

2)  3x – 2(0) = –4
              –2y = –4                          3x = –4
                  y = 2                   x =
y-intercept = (0, 2) x-intercept = (–1, 0)

Graph using the x- and y-intercepts:

Stop!  Go to Questions #12-17 about this section, then return to continue on to the next section.


Point-Slope Form

When given certain information about a line, it is possible to find the equation of the line by using the point-slope form.  Let's take a look at two possibilities.


Given the slope and a point on the line, find the equation of the line.

Replace x1 , y1 and m with the given point and the given slope, and then solve for y.

Example #1:  Write the equation of a line that contains the point (–3, –4) and has a slope of .


The equation of the line passing through the point (–3, –4) with a slope of is y = x – 2.

Given two points, find the equation of the line.

Example #2: Write an equation of a line containing the points (2, 1) and (5, 4).

Use the slope formula for finding the slope when given two points.



Choose one of the points (2, 1) OR (5, 4).

Replace x1 , y1 and m with the given point and the given slope, and then solve for y.

We’ll use point (2, 1).


The equation of the line passing through (2, 1) and (5, 4) is y = x – 1 in slope‑intercept form.   

question1What would the equation look like in standard form?

–x + y = –1

"Click here" to check the answer.


question1The equation could be transformed into an equivalent equation in simpler form by multiplying both sides by –1.  What would that equation look like?

x – y = 1

"Click here" to view both graphs.




Now, let’s apply what we have learned to a real life situation.


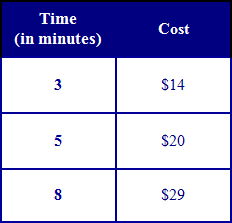
Example #3:  While visiting NYC, Merna created the following chart based on her cab rides.  Write an equation in slope-intercept form that would represent any cab ride and then find the cost for a 7 minute cab ride using the linear equation. 


Find the equation:

First select ANY two ordered pairs from the chart to find the slope or rate of change:

Let's use (3, 14) and (8, 29).
 
m =     m = = 3
 
The cost per minute is $3.  This is the slope of the equation.   
Now, use point-slope formula to write the linear equation.  Be sure to use one of the points PREVIOUSLY selected. 

We'll use (8, 29) for the point.  We now know the slope, m = 3.

y – y1 = m(x –x1) Point-slope Formula
y – 29 = 3(x – 8) Substitute x1= 5, y1= 29, m = 3
y – 29 = 3x – 24 Distribute.
y = 3x + 5 Add 29 to both sides of the equation.

Use the equation to find the cost of a 7-minute ride in New York City.

   
y = 3x + 5  
y = 3(7)+ 5 Substitute. (x = 7)
y = 26 Simplify.
   

So, a 7-minute cab ride in New York City would cost $26!



Stop!  Go to Questions #18-25 about this section, then return to continue on to the next section.


Equations of Horizontal and Vertical Lines

Let's revisit the slopes of horizontal and vertical lines and take a closer look.

Horizontal lines have a slope of 0.
 
Vertical lines have an undefined slope or no slope.

In this unit, we will discuss the equation of both of these lines and how to graph each.


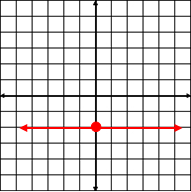
Example #1:  Graph y = –2.

This is a horizontal line with a y-intercept of (0, –2).
 
Plot the point (0, –2) and draw a horizontal line through it.


Notice that the line is flat.  It has a slope of zero.  In slope-intercept form, the equation of the line would be y = 0x –2; thus, the equation is simply, y = –2. 

Notice that all of the points on the line have a y-coordinate of –2;  thus, y = –2. 


question1What are the coordinates of a few points on this line?

Sample Answer: (0, –2), (–5, –2), (3, –2), (100, –2)

"Click here" to check the answer.



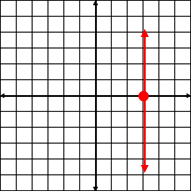
Example #2:  Graph x = 3.

This is a vertical line with an x-intercept of (3, 0).
 
Plot the point (3, 0) and draw a vertical line through it.


Notice that all of the points on the line have an x-coordinate of 3;  thus, x = 3. 


question1What are the coordinates of a few points on this line?

Sample Answer: (3, 0), (3, –4), (3, 10), (3, –1000)

"Click here" to check the answer.





Stop!  Go to Questions #26-30 about this section, then return to continue on to the next section.


Parallel and Perpendicular Lines

Parallel lines have the same slope.

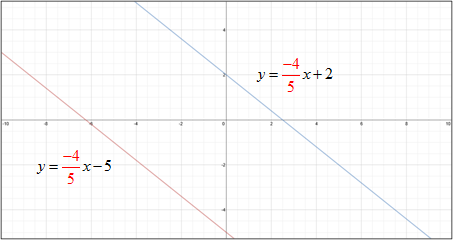
Example #1:  Are the graphs of these two linear equations parallel?

y = x – 5  and  y = x + 2

Yes, these two lines are parallel because each has a slope of .

The graph shows that the lines are parallel. 


Perpendicular lines have opposite reciprocal slopes.

Example #2:  Are the graphs of these two linear equations perpendicular?

y = x +2  and  y = x – 3

Yes, the graphs are perpendicular lines because and are opposite reciprocals.


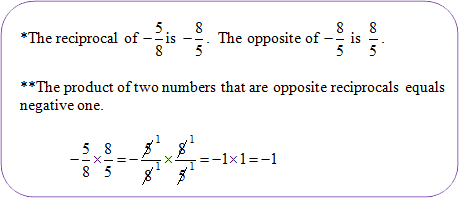Let’s look at the graphs of the above lines. 

Do the lines appear to be perpendicular?  Do they cross at right angles? 



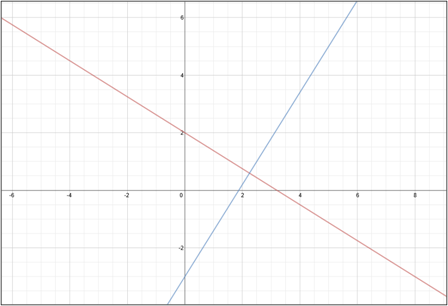The graph appears to show that the lines are perpendicular; BUT, to be sure, we must check that the slopes are opposite reciprocals.  A second check is to multiply the slopes to be sure that equal negative one.

By knowing this, you will be able to identify and write equations of lines that are parallel to or perpendicular to given equations and containing a certain point.

Example #3:  What is the slope of a line that is parallel to 4x – 5y = 10?

Arrange the equation in slope intercept form.  (y = mx + b)


*Remember, parallel lines have the same slope.

Now, identify the slope (m).

y = mx + b     y = x – 2     m =

The graph of any linear equation with a slope of will be parallel to 4x – 5y = 10.

Example #4:  What is the slope of a line that is perpendicular to 4x – 5y = 10?

*Remember, the slopes of perpendicular lines are opposite reciprocals. 

Examine the slope-intercept form of this equation determined in Example #3.

y = mx + b     y = x – 2     m =

The opposite reciprocal of is .     Note:   × = = –1

The graph of any linear equation with a slope of will be perpendicular to 4x – 5y = 10.

Example #5:  What is the equation of a line that is parallel to y = 2x + 3  and passes through the point (–1, 4)?  Put the equation in slope-intercept form.

Determine the slope of the given equation.

y = 2x + 3 has a slope of 2, so m = 2.

Since we want a line parallel to this line, we will use the same slope m = 2 because parallel lines have the same slope.

Use the point-slope formula and substitute the slope (m = 2) and the given point (–1, 4) to determine the equation.

y – y1 = m(x – x1) m = 2, x1 = –1, y1 = 4
y – 4 = 2(x – (–1)) Substitute.
y – 4 = 2(x + 1) Simplify.
y – 4 = 2x + 2 Distribute.
y = 2x + 6 Add 4 to both sides and simplify.

The equation of a line that is parallel to y = 2x + 3 and passes through the point (–1, 4) is
y = 2x + 6. 

Example #6:  What is the equation of a line that is perpendicular to 5x + 2y = 10 and passes through the point (3, –5)?  Put the equation in slope-intercept form.

Solve the equation 5x + 2y = 10 for y and determine the slope.

5x + 2y = 10  
2y = –5x + 10 Subtract 5x from both sides and simplify.
y = x + 5 Divide both sides by 2 and simplify.

The slope of this line is .  We want to use the opposite reciprocal because we want the equation of a line perpendicular to the given equation.

The opposite reciprocal of is .

Use the point-slope formula and substitute the slope (m = ) and the given point (3, –5) to determine the equation.

y – y1 = m(x – x1) m = , x1 = 3, y1 = –5
y – (–5) = (x – 3) Substitute.
y + 5 = (x – 3) Simplify.
y + 5 = x – Distribute.
y = x – – Subtract 5 from both sides.
y = x – Simplify.

The equation of a line that is perpendicular to 5x + 2y = 10 and passes through the
point (3, –5) is y = x – .

Now, let’s apply what we have learned to a real life situation.

Example #7:  Sharon is designing a quilt using graph paper.  Some of the lines need to be parallel and others need to be perpendicular.  Decide which of the linear equations Sharon should select to make parallel lines and perpendicular lines for the quilt.

5x + 2y = 8          y = 7 + x          3x + 4y = 8          5x = –2y – 3

Put all equations into slope-intercept form by solving for y:

5x + 2y = 8 y = x + 7 3x + 4y = 8

5x = –2y – 3
2y = –5x + 8   4y = –3x + 8 5x + 3 = –2y
y = – x + 4   y = – x + 2 x + = y
      y = – x +

Answer:  Sharon should use the first and last lines for the parallel section because the lines have the same slope ( ).  She should use the second equation with the first and last equations because their slopes are opposite and reciprocals which would make them perpendicular lines.  The third equation would not be used in making the quilt. 



Stop!  Go to Questions #31-40 to complete this unit.



Below are additional educational resources and activities for this unit.
 
Solve for y
 
Graphing Using Standard Form
 
Converting Slope Standard and Point Slope