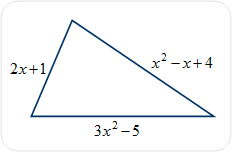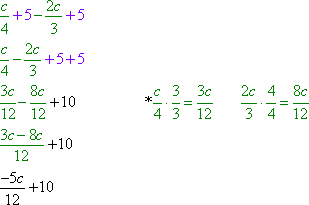PDF

POLYNOMIALS


Unit Overview
This unit is an introduction to polynomials.  In this unit you, will learn how to add and subtract polynomials.  This concept will be expanded upon in future units and is very important to understand.


Polynomials

In the previous unit, you learned about monomials.  In this unit, we are going to combine monomials with addition and subtraction and identify them with other names.

You have learned that a number, 3, a variable, x, or a product of a number and variable(s), 5mn, are called monomials.  At this point, it should be mentioned that to be considered a monomial, a variable cannot have a negative exponent or appear in the denominator of a rational number.

For example, the following are not monomials:  x–4 and .

In this unit you, will be working with expressions like the following:

5m – 2
4x2 + 7x – 3
–5a2b3 + ab

Each of these is a sum or difference of monomials called a polynomial.


Special Names of Some Polynomials

Each monomial within a polynomial is called a term.  A polynomial with exactly two terms is called a binomial and a polynomial with exactly three terms is called a trinomial.

Example #1:  y2 + y is a polynomial and can be called a binomial because it has two (2) terms.
 
Example #2:  is not a polynomial because the variable x is in the denominator of the term .
 
Example #3:   is a binomial because it has two (2) terms and no variables appear in the denominator of the fraction.
 
Example #4:  3x2 + 6x + 5 is a polynomial and can be called a trinomial because it has three (3) terms.

Recall that the numerical factor of a monomial is called the coefficient.  In the term, –2y3 y, –2 is the coefficient.

Example #5:  Identify the terms and give the coefficient of each term.

4x3 + 5x2 – 3
 
The terms are 4x3, 5x2, and –3.
 

The coefficient of 4x3 is 4 and 4 and x3 are factors, the coefficient of 5x2 is 5 and 5 and x2 are factors, and the constant term is –3.

question1What are the coefficents of each of the variable terms in 7y3 + 4y2 – 9y + 5?

7, 4, and –9

"Click here" to check the answer.


Quicktime_Video_Icon  General Polynomials (02:14)

Example #6:  A local cell phone company uses the following expression when calculating cell phone charges.  Interpret what each part of this expression may represent using correct mathematical terminology.
0.20t + 25
Answer:  The cell phone company may charge a monthly flat fee of $25 which is seen as the constant in the expression.  In addition, they charge 0.20 per text. 

0.20 is the coefficient of the expression 0.20t of which 0.20 and t are factors.  The number of text messages could be represented by t.


Simplifying Polynomials

To simplify polynomials, we collect like terms. Recall that terms like 3xy2 and 7xy2, whose variable factors are exactly the same, are called like terms.  To simplify like terms, we combine the coefficients.

Example #7:  Simplify 3m3 – 5m3.

3m3 – 5m3 =
   
  = (3 – 5)m3
   
  = –2m3
 
Example #8:  Simplify 7x5y4 – 6y3 – 2x5y4 + 3y3.

= 7x5y4 – 6y3 – 2x5y4 + 3y3
 
= 7x5y4 – 2x5y4 – 6y3+ 3y3
 
= (7 – 2)x5y4 + (–6 + 3)y3
 
= 5x5y4 + (–3y3)
 
= 5x5y4 – 3y3

In future units, it will be necessary to determine the degree of a term or polynomial; so, at this point, we will talk about the degree of terms and polynomials.  The degree of a term is found by adding all the exponents of the variables.  The degree of a polynomial is then determined by the highest degree of all its terms.

Finding the Degree of a Polynomial

The degree of a polynomial is the highest degree of its terms.  The degree of a term is the sum of the exponents of the variables that appear in it.

Example #9:  Find the degree of the monomial 7x4y3z..

= 7x4y3z1

*z = z1

*If the exponent is not shown, you must assume that it is 1.

-add the exponents 4 + 3 + 1

The degree of this monomial is 8. 
 
Example #10:  Find the degree of the polynomial 8a4b2 – 4ab + 7.

There are three terms in this polynomial, so check the degree of each term.  The degree of the polynomial is the highest degree that occurs in any of its three terms.

- degree of 8a4b2 is 4 + 2 = 6  
   
- degree of 4ab is 1 + 1 = 2 *4ab = 4a1b1
   
- degree of 7 is 0 (because there are no variables)

Therefore, the degree of 8a4b2 – 4ab + 7 is 6.
               
*Remember:  The degree of a polynomial is determined by the highest degree that occurs in any one of its terms

question1What is the degree of 7xy3 + 4x4y2 – 9xy + 5 ?

The degree is 6 based on the second term (4 + 2 = 6).

"Click here" to check the answer.



Order of a Polynomial

Polynomials are generally written in either descending order (largest to smallest) in terms of a variable or ascending order (smallest to largest).

Example #11:  For each of the given polynomials, determine the order of the polynomial in terms of x.

a.)  –3x3y + 4x2y2 + 5xy3 – 9y

 This polynomial is written in descending order for the variable x because the exponents of x are aligned largest to smallest.
 
      –3x3y + 4x2y2 + 5xy3 – 9y
b.)  –7x + 9x2y + 3x3y2 – 14x4

 This polynomial is written in ascending order for the variable x.

      –7x + 9x2y + 3x3y2 – 14x4

question1In terms of y, what is the order of –2x3y + 8x2y2 + 7xy3 – 9y4 ?

Ascending Order

"Click here" to check the answer.


Stop!  Go to Questions #1-17 about this section, then return to continue on to the next section.


Adding Polynomials

We are going to add and subtract polynomials in the same way that we simplified expressions, by combining like terms.  Follow along with the examples below.

Example #1:  Find the sum:  (6x – 5y) + (–7x + 3y).

This sum equals the single polynomial:

6x – 5y – 7x + 3y          *+( –7x) = –7x and +(+3y) = +3y

Rearrange the terms so that like terms are beside each other:
6x – 7x – 5y + 3y         

Collect like terms:

(6+ –7)x + (–5 + 3)y         
 
–1x + (–2y)          * –1x = –x and +(–2y) = –2y
 
–x – 2y    

Example #2:  Find the sum  .

This sum equals the single polynomial:


Rearrange the terms so that like terms are beside each other:

Express the rational numbers with a common denominator (15).

 

Collect like terms:

*t = 1t
   
Continue on to simplify the first term.
   

Example #3:  Find the sum:  (3x2 – 15) + (5x2 + 7x).

This sum equals the single polynomial:

3x2 – 15 + 5x2 + 7x

Collect like terms:
(3 + 5)x2 – 15 + 7x
 
8x2 – 15 + 7x

Example #4:  Given the following square with sides of given length, find the perimeter by adding all of the sides.

3j + k

Add all four sides:
P = (3j + k) + (3j + k) + (3j + k) + (3j + k)

The sum equals the single polynomial:

P = 3j + k + 3j + k + 3j + k + 3j + k

Collect like terms:

P = 3j + k + 3j + k + 3j + k + 3j + k
 
   = (3 + 3 + 3 + 3) j + (1 + 1 + 1 + 1) k
 
   = 12j + 4k

The perimeter of the given rectangle is 12j + 4k.

Example #5:  Given the following triangle with sides of given length, find the perimeter by adding all of the sides.


Add all three sides:

P = (2x + 1) + (x2 – x + 4) + (3x2– 5)

The sum equals the single polynomial:

P = 2x + 1 + x2 – x + 4 + 3x2 – 5

Collect like terms:

P = 2x – x + 1 + 4 – 5 + x2+ 3x2
 
   = (2 – 1)x + (1 + 4 – 5) + (1 + 3)x2
 
   = x + 0 + 4x2

Write in descending order of x:

P = 4x2 + x

The perimeter of the given rectangle is 4x2 + x.

Stop!  Go to Questions #18-24 about this section, then return to continue on to the next section.


Subtracting Polynomials

 Subtracting polynomials is done with the same process as adding in the fact that you will combine like terms.  Be very careful when subtracting a quantity to make sure you subtract each term within the quantity.

 *It is very helpful to change all the signs of the quantity being subtracted, and then combine like terms.  Follow along with the example below.
Example #1:  Find the difference: (8t – 4s) – (3t – 5s).

Change to addition, reversing all the signs of the terms in the second quantity
(3t – 5s) to the opposite sign.

8t – 4s + (–3t + 5s)

Collect like terms:

8t – 4s – 3t + 5s
 
8t – 3t – 4s + 5s
  
(8– 3)t + (–4 + 5)s
 
5t + 1s
 
5t + s          *1s = s

Example #2:  Find the difference:  .

Change to addition, making all of the signs of the terms in the second quantity the opposite sign:


Collect like terms:


Example #3:  Find the difference: (5x4 + 3x2) – (6x4 –2x2).

Change all the signs in the second quantity:

5x4 + 3x2 + (–6x4 + 2x2)

Collect like terms:

5x4 – 6x4 + 3x2 + 2x2
 
(5 – 6)x4 + (3 + 2)x2
  
–x4 + 5x2

Example #4:  Find the difference: (–7m3 + 2m + 4) – (–2m3 – 4).

Change all the signs in the second quantity:

–7m3 + 2m + 4 + (+2m3 + 4)

Collect like terms:

–7m3 + 2m + 4 + 2m3 + 4
 
(–7 + 2)m3 + 2m + (4 + 4)
  
–5m3 + 2m + 8


Are Polynomials Closed?

The closure property states that when two elements are combined with a given operaion, the result is another element of that same set.  For example, when you add 7 + 3 (which are both whole numbers) the result 10 is also a whole number; hence the whole numbers are closed under addition.  

So with polynomials, when you add two polynomials, will the result still be a polynomial?  Before answering, review the examples in the content section titled "Adding Polynomials" to see if each answer was also a polynomial.

question1Are polynomials closed under addition?

Yes!

"Click here" to check the answer.


Now, consider subtraction of polynomials for closure.  Look over the answers to the subtraction examples in this section of the content.  When two polynomials are subtracted, will the result always be a polynomial?

question1Are polynomials closed under subtraction?

Again, Yes!

"Click here" to check the answer.


Stop!  Go to Questions #25-37 to complete this unit.


Below are additional educational resources and activities for this unit.
 
Naming Polynomials
 
Adding and Subtracting Polynomials Worksheet 1
 
Adding and Subtracting Polynomials Worksheet 2