PDF

INEQUALITIES AND MEASUREMENTS


Unit Overview
In this unit, you will use the procedure to solve multi-step equations to solve multi-step inequalities and graph solutions on the number line.  You will then examine how to convert measurements using dimensional analysis, a method used often in scientific studies.  The study of measurement ends with a look at the exactness of a measurement and how to allow for variances.


Solving Multi-step Inequalities

Inequality - a mathematical statement that compares algebraic quantities.


*Solving inequalities is just like solving equations, use opposite operations to isolate the variable.

Quicktime_Video_Icon  Solving Inequalities (04:12)

Example #1:  Solve the inequality for x:  3(5x – 7) ≥ 54

3(5x – 7) ≥ 54  
 15x – 21 ≥ 54 Apply the distributive property to the left side.
       +21    +21 Add 21 to both sides of the inequality.
 15x         ≥ 75 Simplify.
          ≥ Divide both sides of the inequality by 15.
             x ≥ 5  

*When multiplying or dividing by a negative number, the inequality sign must be reversed.

Let’s take a look at why this rule applies.

Let’s say that we know 4 > 2.  If we multiply both sides of this inequality by a –2, let’s see what happens to the inequality.

      4 > 2 *this is a true inequality
   
(–2)4 > (–2)2 multiply both sides by –2
   
     –8 > –4
          		 *the result is not a true statement; however, if we flip the inequality sign, the result will be a true statement.
     –8 < –4  

Example #2  Solve the inequality for y:  2y + 9 < 5y + 15

  2y + 9 < 5y + 15  
–5y        –5y Subtract 5y from both sides of the inquality.
–3y + 9 < 15 Simplify.
        –9    –9 Subtract 9 from both sides of the inquality.
        –3y < 6 Simplify.
        < Divide both sides of the inequality by –3.
            y > –2 Flip the inquality symbol because of the division by a negative number (–3).

Example #3:  Solve the inequality for x:  (x – 7) ≤ x – 3

(4) (x – 7) ≤ 4(x – 3) Multiply both sides by 4 to eliminate the fraction.
      3(x – 7) ≤ 4(x – 3) Distribute.
     –3x – 21 ≤ 4x – 12 Simplify.
     –3x          –3x Subtract 3x from both sides of the inequality.
             –21 ≤ x – 12 Simplify.
             +12        +12 Add 12 to both sides.
               –9 ≤ x Simplify.
                 x ≥ –9 Rewrite with x on the left side, the inequality sign is reversed.

You can represent the solution of an inequality in one variable on a number line.

For < and > an open circle is used to denote that the solution number is not included in the solution.

For ≤ and ≥ a closed circle is used to denote that the solution number is included in the solution.

Example #4: 
x < 4    
y ≥ –7

 
 
 

Stop!  Go to Questions #1-9 about this section, then return to continue on to the next section.


 Measurement

In the real world, measurements can seldom be exact. Sometimes, it is impossible to measure exactly because of the measurement tool. Other times, it is simply more expedient (easier) not to use an exact measurement. This gives us three types of measuring: 



Exact Measurement:  The numbers used are literal and no margin of error is used when determining the answer.

Estimation:  The problem would be much easier to solve if we round some of the numbers and the information provided by rounding is still accurate enough to provide the answer needed.

Approximation:  When the measuring device is not accurate enough or the number in the problem is perhaps irrational (such as pi), then we approximate to the best of our ability.

Artworks makes flags for the football team.  Consider each of the given scenarios about creating the flag and  determine which type of accuracy is best described.

Artworks needs to determine how much material to order.  They know that 1500 flags will be printed so they take 18 × 15 (finding area) × 1500.

question1What type of measurement is used to determine the amount of material to order?

Estimation because they just needed an estimate to order the material.

"Click here" to check the answer.



question1What type of measurement is used to determine the amount that will be collected?

Exact, both numbers are used to state an exact amount determined.

"Click here" to check the answer.





question1What type of measurement is used?

Approximation, this is as accurate as the measuring tape will show.

"Click here" to check the answer.



Note:  In determining the type of measurement, another factor considered is that the measurement is accurate enough to make the design on the computer.

Quicktime_Video_Icon  Exact Number Needed -- Steel Beams (04:12)

Quicktime_Video_Icon  Adequate Estimates -- Wedding Food (01:12)

Quicktime_Video_Icon  Flexibility -- Travel Budget (01:59)

Stop!  Go to Questions #10-12 about this section, then return to continue on to the next section.


Relative Error

Because no measurement is “exact,” we will examine how to find the relative error.

Relative error is the ratio of the absolute value of the difference of a measured value and and actual value, compared to the actual value. 

When relative error is expressed as a percent, it is called percent error. 
 
*Note:  The absolute value sign is used to provide a positive amount because we are not concerned if the value is over or under the actual value.

When dealing with measurements, the greatest possible error it is always of the unit in both directions.

Example:  The floor plan below shows the measurements for a new home with the Family Room  measuring a rectangular area of 12 ft by 14 ft.  What is the greatest possible percent error in finding the area of the room? 


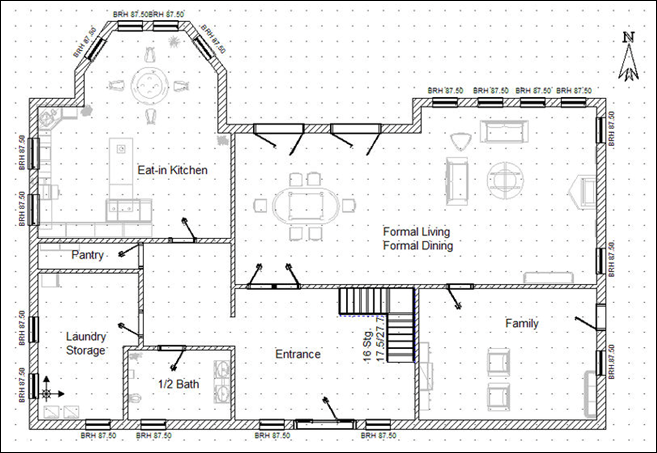Calculate the measured area.
A = lw
A = 12(14)
A = 168 sq ft

Calculate the minimum area with a greatest possible error of 1/2 ft. Calculate the maximum area with a greatest possible error of 1/2 ft.
   
     l = 12 − ft         w = 14 − ft      l = 12 + ft         w = 14 + ft
   
A = lw
A = 11.5(13.5)
A = 155.25 sq ft
A = lw
A = 12.5(14.5)
A = 181.25 sq ft

Find the differences:
| minimum area | − | measured area | = | 155.25 − 168 | = | −12.75 | = 12.75 sq ft
 
| maximum area − measured area | = | 181.25 − 168 | = | −13.25 | = 13.25 sq ft

Use the GREATER possible difference to compute the relative error.  In this example, the greater difference in area is 13.25.

Quicktime_Video_Icon  Introduction: Error in Foam Making (01:57)

Quicktime_Video_Icon  Absolute and Relative Error -- Construction (03:02)

Quicktime_Video_Icon  Importance of Errors -- Emergency Room (01:58)

Quicktime_Video_Icon  Low Tolerance for Error -- Drag Racing (01:45)

By changing the ratio to a percent we can see the greatest possible percent error in area, based on measurements to the nearest foot, is about 8%. 

Stop!  Go to Questions #13-15 about this section, then return to continue on to the next section.


 Measurement Conversions 

Study the below example of using conversion factors to accurately compare or convert units. 

Example:  Ozlem Kaya of Turkey ran the Steeplechase of 2000 meters in 10.05 minutes while Emma Coburn of the US ran the race of 1.242 miles in 567 seconds.  Who had the better time? 

To compare the two times select one of the athletes and use conversions factors until you have the same units. 

We will begin with Emma’s time.  Emma's time is given in miles and seconds.  We will convert her time to meters and minutes so that we can compare her time with Ozlem's time.

We will use the process of dimemnsional analysis where we use equivalent measures of time and distance in fractional form.

First, let's examine what we have and where we want to end.

Emma's time:  1.242 miles in 567 seconds  

Ozlem's time: 2000 meters in 10.05 minutes

So, we need to consider the conversion factors for:

miles meters seconds minutes
1 mile = 1610.305 meters 60 seconds = 1 minute

Now, let's see how dimensional analysis can help us make this conversion.


As we look over the cancellations, we see that we still have the units of meters and minutes. We need to compare Emma's time with Ozlem's time.

Now, we must multiply the numbers in the numerator and denominator to make the conversion.


Now, we have numbers to compare that are in the same units.

Ozlem's time:   Emma's time:  

 Can you tell who was faster?

Let's convert both to unit rates (denominator equals 1) to determine the faster time.

Ozlem's unit rate:
 
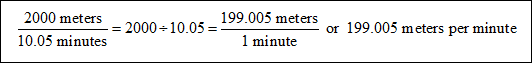Emma's unit rate:
 
Thus, Emma ran at a faster rate to complete the Steeplechase in the 2012 summer Olympics.

Quicktime_Video_Icon  Practice Problem: Unit Conversion Factors (01:07)

Quicktime_Video_Icon  Performing Multiple Unit Conversions (03:50)

Quicktime_Video_Icon  Practice Problems: Unit Conversions (05:22)

Stop!  Go to Questions #16-26 to complete this unit.



Below are additional educational resources and activities for this unit.
 
Multi-step Inequalities
 
Measurement Conversions