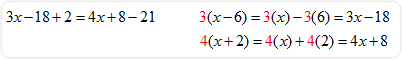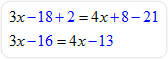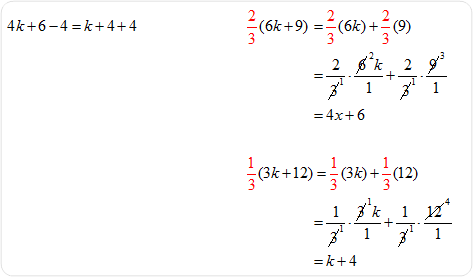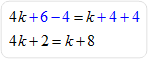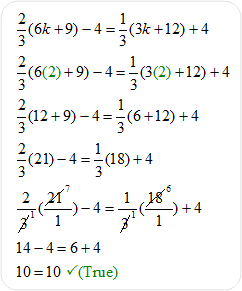INTEGERS AND EQUATIONS
 |
Unit Overview
In this unit, you will review integers and the rules that apply to adding, subtracting, multiplying and dividing these special numbers. You will also learn about equations and how the Real Number Properties of Equality justify the steps to solve an equation. You will also solve literal equations and formulas.
Comparing Integers
The set of whole numbers consists of 0, 1, 2, 3 … and can be represented on a number line. We can match each whole number with another number that is the same distance from 0 but on the opposite side of 0.
 |
If you take a look at the number line above, 3 or (positive 3) and –3 (negative 3) are on opposite sides of 0 but the same distance from 0. These numbers are called opposites and make up the set of integers. Integers are the set of positive and negative whole numbers.
Examples: Name the integer that is suggested by each situation.
|
To compare integers, we will use the symbol “<” which means less than or the symbol “>” which means greater than. If you remember from the previous unit, these symbols are called inequality signs. An inequality can either be true or false. For example, the sentence 12 > 8 is true and the sentence 6 > 9 is false.
On a number line, the numbers increase as you move from left to right. For any two numbers, the number that is farther to the right is the larger number and the number farther to the left is the lesser number. Let’s take a look at comparing some integers using the number line below.
 |
Write a true sentence using < or > in place of
|
|||||||||||||||||||||||||||||||||
Hint: An easy way to remember the direction of the inequality sign is that it always points to the smaller number.
If you study the number line above, you will notice that the integers 5 and –5 are the same distance from 0. This brings us to another algebraic concept called absolute value. The absolute value of a number is the distance it is from 0, which means that the absolute value will always be positive. Absolute value is symbolized by using two straight bars around a number.
| Example #1: | |24| means the absolute value of 24, which is 24 because 24 is 24 units away from 0. |
| Example #2: | |–57| means the absolute value of –57, which is 57 because –57 is 57 units away from 0. |
Stop! Go to Questions #1-6 about this section, then return to continue on to the next section.
Adding and Subtracting Integers
When adding and subtracting integers, it will be very helpful to understand the following rules:
Adding Integers |
Same sign: If the numbers have the same sign, add the numbers and keep the sign given.
|
Different signs: If the numbers have different signs, subtract the absolute value of the numbers and use the sign of the larger absolute value.
|
Subtracting Integers |
Change the problem to addition and add the opposite of the second number. Then go to addition rules.
| Example #1: | 15 – (–8) = |
|
| 15 + (–8) = | change the problem to addition | |
| 15 + (+8) = | change (–8) to a (+8) | |
| 23 | Add the numbers because they now have the same sign. |
|
| Example #2: | 18 – 26 = | |
| 18 + (26) = | change the problem to addition |
|
| 18 + (–26) = | change 26 to (–26) |
|
| –8 | Subtract the numbers because they now have different signs and use the sign of the larger absolute value. |
Stop! Go to Questions #7-12 about this section, then return to continue on to the next section.
Multiplying and Dividing Integers
The rules for multiplying and dividing integers are a little easier to remember because there are only two rules.
Same sign: If the numbers have the same sign, the answer will be positive.
|
Different signs: If the numbers have different signs, the answer will be negative.
|
*When multiplying more than one number, it may be helpful to remember the following rule in determining the sign of your answer:
|
| Example #1: | (–4)(–3)(5)(–2) |
| Since there are 3 negative signs, the answer to this will be negative. | |
| Let’s check it out by multiplying from left to right. | |
| (–4)(–3)(5)(–2) | |
| (12)(5)(–2) | |
| (60)(–2) | |
–120 |
|
| Example #2: | (–2)(–4)(–3)(–2) |
| Since there are 4 negative signs, the answer to this will be positive. | |
Let’s check it out by multiplying from left to right. |
|
(–2)(–4)(–3)(–2) |
|
(8)(–3)(–2) |
|
(–24)(–2) |
|
48 |
Stop! Go to Questions #13-16 about this section, then return to continue on to the next section.
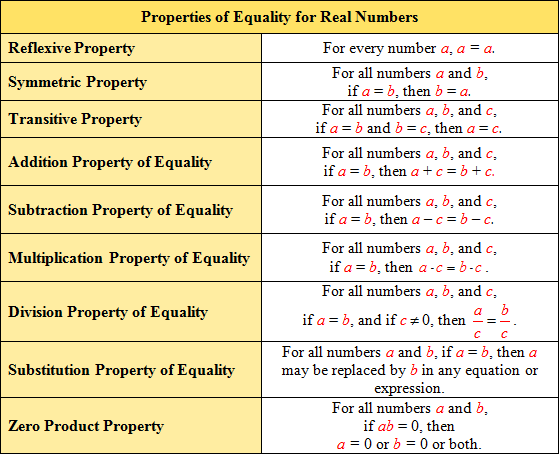
Real Number Properties of Equality
In the table below, each of the properties of equality for real numbers are listed with a general explanation of each property. The properties are used to verify steps in solving equations.
Study the Properties of Equality and then answer the questions in the interactive examples below.
 |
| Examples: For each statement below, assume all variables represent real numbers. Identify each property illustrated by the statement. |
![]() If x = y, then x + 7 = y + 7.
If x = y, then x + 7 = y + 7.
Addition Property of Equality
"Click here" to check the property.
![]() If x = y and y = 8, then x = 8.
If x = y and y = 8, then x = 8.
Transitive Property of Equality
"Click here" to check the property.
![]() If x = y, then x(7) = y(7).
If x = y, then x(7) = y(7).
Multiplication Property of Equality
"Click here" to check the property.
![]() 15 = 15
15 = 15
Reflexive Property
"Click here" to check the property.
![]() If x = y, then
If x = y, then ![]() .
.
Division Property of Equality
"Click here" to check the property.
![]() If x = 10, then 10 = x.
If x = 10, then 10 = x.
Symmetric Property of Equality
"Click here" to check the property.
![]() If x = y + 4 and y = 6, then x = 6 + 4 = 10.
If x = y + 4 and y = 6, then x = 6 + 4 = 10.
Substitution Property of Equality
"Click here" to check the property.
![]() If x = y, then x – 7 = y – 7.
If x = y, then x – 7 = y – 7.
Subtraction Property of Equality
"Click here" to check the property.
![]() If 9x = 0, then 9 = 0 (not true) or x = 0; thus, x = 0.
If 9x = 0, then 9 = 0 (not true) or x = 0; thus, x = 0.
Zero Product Property
"Click here" to check the property.
The properties of real numbers will be very useful in solving equations algebraically.
Stop! Go to Questions #17-18 about this section, then return to continue on to the next section.
Solving Basic Equations
In the first unit, you learned that there is a specific order in which mathematical operations are performed in simplifying expressions. In this section, you are going to learn that to solve an equation involving more than one operation. You must perform the order of operations IN REVERSE to solve for the unknown variable.
Let’s first review solving one-step equations.
Example #1: Solve for y – 6 = –21 for y.
Therefore, y = –15 in the equation y – 6 = –21. |
Example #2: Solve for
Therefore, m = –15 in the equation |
In the next few examples, we are going to combine the two processes from above in one equation. Remember, that to solve an equation; you must perform the order of operations in reverse order, which means:
|
Example #3: Solve for 5x + 6 = 31 for x.
Check the answer by replacing x with 5 in the original equation.
Therefore, x = 5 in the equation 5x + 6 = 31. |
Stop! Go to Questions #19-22 about this section, then return to continue on to the next section.
Literal Equations/Formulas
As we have seen in the previous unit, sometimes in math and science it is necessary to rewrite an equation or a formula to highlight another quantity of interest. We will now investigate when the literal equation/formula has several unknown variables and more than one property of equality is needed to isolate the quantity of interest.
|
The formula for finding the perimeter of a rectangle is P = 2L + 2W.
Let’s examine how to solve for L if it is the quantity of interest.
 |
Now, let's solve the perimeter formula of a rectange for W.
| P = 2L + 2W |
![]() What is the quantity of interest?
What is the quantity of interest?
" W "
"Click here" to check the answer.
![]() What inverse operation should be done first?
What inverse operation should be done first?
Subtract 2L from both sides.
"Click here" to check the answer.
![]() What is the simplifed equation after performing the first inverse operation?
What is the simplifed equation after performing the first inverse operation?
P – 2L = 2W
"Click here" to check the answer.
![]() What inverse operation should be done next?
What inverse operation should be done next?
Divide both sides by 2.
"Click here" to check the answer.
![]() What is the final equation of the perimeter formula solved for W ?
What is the final equation of the perimeter formula solved for W ?
W = (P – 2L) / 2
"Click here" to check the answer.
| Example #2: If the perimeter of a rectangle is 48 centimeters and the length of is 15 centimeters, what is the width of the rectangle? In the previous scenario, we solve the perimeter formula for W. We will use this formula to make our work easier!
Now, the problem is just a matter of substituting, then evaluating to find the solution.
The width of the rectangle is 9 centimeters. Let's check our answer using the original formula.
|
Stop! Go to Questions #23-24 about this section, then return to continue on to the next section.
Solving Equations with Variables on Both Sides
Example #1: Solve for 4x – 7 = 8 – x for x.
Check the answer by replacing x with 3 in the original equation.
Therefore, x = 3 in the equation 4x – 7 = 8 – x. |
|
 Total purchase of both teens = Total cost 2 x + 2x + 16 = $72 Equation: 2x + 2x + 16 = 72 Solution:
The cost of a pack of guitar strings is $14.00. |
Example #3: Solve for 13 + 4x = –2x – 5x + 79 for x.
Check the answer by replacing x with 6 in the original equation.
Therefore, x = 6 in the equation 13 + 4x = –2x –5x + 79. |
To extend the process of solving equations, there may be times when you will have to use the distributive property first to eliminate any parentheses. You will then combine any like terms and solve. Take a look at the example below.
Example #4: Solve for 5(d + 4) = 7(d – 2) for d.
Check the answer by replacing d with 17 in the original equation.
Therefore, d = 17 in the equation 5(d + 4) = 7(d – 2). |
Example #5: Solve for 3(x – 6) + 2 = 4(x + 2) – 21 for x.
Check the answer by replacing x with –3 in the original equation.
Therefore, x = –3 in the equation 3(x – 6) + 2 = 4(x + 2) – 21. |
Example #6: Solve for
Check the answer by replacing k with 2 in the original equation.
Therefore, k = 2 in the equation |
Stop! Go to Questions #25-33 to complete this unit.



 W
W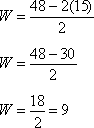

 Example #2: Carley and Nathan are shopping for new guitar strings at the local music store. Nathan buys 2 packs of strings. Carley buys 2 packs of strings and a music book. The book costs $16. Their total cost is $72. How much is one pack of strings?
Example #2: Carley and Nathan are shopping for new guitar strings at the local music store. Nathan buys 2 packs of strings. Carley buys 2 packs of strings and a music book. The book costs $16. Their total cost is $72. How much is one pack of strings?