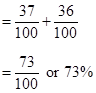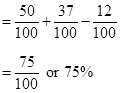INDEPENDENT AND DEPENDENT EVENTS; CONDITIONAL PROBABILITY
 |
Unit Overview
In this unit you will determine if events are mutually exclusive or inclusive along with calculating probabilities of dependent and independent events, and conditional probabilities.
Using Addition with Probability
Inclusive events are events that can occur at the same time. For example, a person can belong to more than one club at the same time.
Mutually exclusive events are events that cannot occur at the same time. For example, if you flip a coin, you cannot get both heads and tails.
|
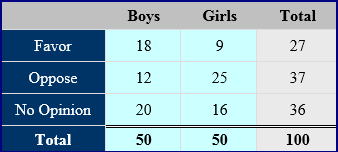
Example #1: In a survey about a change in cafeteria food, 100 students were asked if they favor the change, oppose the change, or have no opinion about the change. The responses are indicated below.
Find the probability that a randomly selected respondent to the survey opposes or has no opinion about the change in cafeteria food. Solution The events “oppose” and “no opinion” are mutually exclusive events. P(oppose or no opinion) = P(oppose) + P(no opinion)
The probability that a respondent opposes the change or has no opinion is 73%. |
| Example #2: Find the probability that a randomly selected respondent to the survey is a boy or opposes the change in the policy. The events “boy” and “opposes” are inclusive events. P(boy or opposes) = P(boy) + P(opposes) – P(boy and opposes)
The probability that a respondent is a boy or opposes the change is 75%. |
The complement of event A consists of all outcomes in the sample space that are not in A and is denoted by Ac. For example, let A be the event “favor”. Then the complement Ac is the event “oppose” or “no opinion”. Conversely, if A is the event “oppose” or “no opinion”, then Ac is the event “favor”. The sum of the probabilities of all the outcomes in a sample space is 1.
Thus, P(A) + P(Ac) = 1
To check this, we will use the survey results given in example 1. Let A be the event “favor”. Verify that P(A) + P(Ac) = 1 is true.
P(A) = 0.27 -favors P(Ac) = 0.37 + 0.36 = 0.73 -opposes or has no opinion P(A) + P(Ac) = 0.27 + 0.73 = 1 |
 |
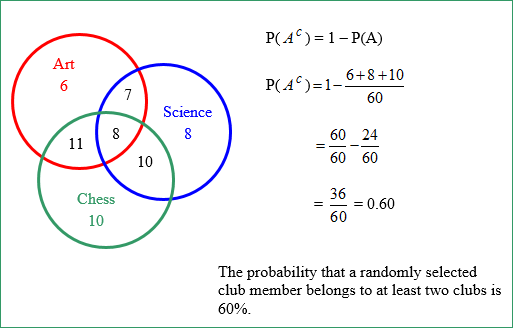
| Example #3: The art, science, and chess clubs have 32 members, 33 members, 39 members, respectively. Some members of each club belong to the other clubs as shown below in the overlapping regions of the Venn diagram. Find the probability that a randomly selected club member belongs to at least two clubs.
|
Stop! Go to Questions #1-12 about this section, then return to continue on to the next section.
Independent Events
Two events are independent if the occurrence (or non-occurrence) of one event has no effect on the likelihood of the occurrence of the other event. For example, rolling a die and choosing a marble out of a bag.
 |
Joint Probability: Understanding the Odds (06:24)Dependent Events
A dependent event is the probability of a second event happening, depending on the outcome of the first event.
 |
 |
Let’s use the conditional probability formula to verify the solutions to the example above.
 |
For the following problems, state whether the events are independent or dependent.
Choosing a winner and runner-up at a talent show.
Dependent, a person can not be both the winner and runner-up.
"Click here" to check the answer.
Roll a die and then spin a spinner.
Independent. The two events do not effect the other.
"Click here" to check the answer.
Tossing a coin three times.
Independent. Tossing a coin does not affect the results of additional tosses of the coin.
"Click here" to check the answer.
Draw a card from a deck of cards and then draw another card.
Dependent. Picking the first card affects the outcome of picking the second card.
"Click here" to check the answer.
Taking a marble from a jar and then taking a second marble without replacing the first marble.
Dependent. Taking the first marble affects what is available to be taken next.
"Click here" to check the answer.
Conditional Probability: The Monty Hall Problem (08:18) Stop! Go to Questions #13-33 to complete this unit.
