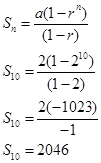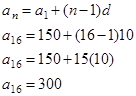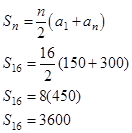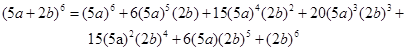SEQUENCES AND SERIES
 |
Unit Overview
An important mathematical skill is discovering patterns. In this unit you will investigate different types of patterns represented in sequences. You will then use the Binomial Theorem to expand powers of binomials.
Arithmetic Sequences
A sequence is a list of numbers in a particular order. Each number in a sequence is called a term. The first term is represented by a1, the second term is represented by a2, and so on. an represents the nth term of the sequence. One kind of sequence is an arithmetic sequence. In an arithmetic sequence each term after the first is found by adding a constant, called the common difference, d, to the previous term.
|
In general, we could write an arithmetic sequence like this:
 |
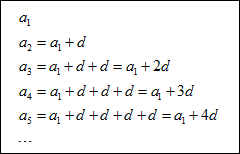We can generalize the expression for an if we realize that the common difference in a sequence of n terms is added to the terms of the sequence n – 1 times. For instance, in the sequence 2, 7, 12, 17, there are 4 terms in the sequence therefore n = 4 and the common difference is d = 5. Starting with the first term and ending with the last, d = 5 is added to the terms a total of 3 times.
2 + 5 = 7 |
7 + 5 = 12 |
12 + 5 = 17 |
For a sequence with n terms, the common difference d is added to the terms in a sequence n – 1 times. From this we obtain the following result:
 |
 |
Introduction: Fashion Sequence (01:33) Arithmetic Sequence -- Pyramids (02:13) Stop! Go to Questions #1-5 about this section, then return to continue on to the next section.
Geometric Sequences
The following is an example of a Geometric Sequence.
2, 22, 23, 24, 25 = 2, 4, 8, 16, 32 |
Another way to look at this sequence is:
a1 = 2, a2 = a1 ⋅ 2, a3 = a2 ⋅ 2, a4 = a3 ⋅ 2, a5 = a4 ⋅ 2 ... |
In each case the next term in the sequence is the product of the previous term and the constant 2. For a Geometric Sequence, the number that multiplies the present term to give the next result is called the common ratio. The effect of the common ratio is perhaps better seen in the next example.
 |
In this example the common ratio is 3 and is denoted r = 3.
Geometric Sequence: A Geometric Sequence is a sequence where each term after the first term, a1, is the product of the preceding term and the common ratio, r, where r ≠ 0 or 1. The terms of a geometric sequence can be represented by;
a1, a2 = a1 ⋅ r, a3 = a2 ⋅ r, a4 = a3 ⋅ r, a5 = a4 ⋅ r ... |
This formula for the general term is as follows:
 |
 |
 |
 |
For the next 4 problems, identify each sequence as arithmetic, geometric, or neither. If the sequence is arithmetic state the common difference. If the sequence is geometric, state the common ratio.
Identify each sequence. 3, –3, 3, –3, ….
Geometric, r = –1
"Click here" to check the answer.
Identify each sequence. 1, 4, 9, 16, …
Neither, the same number is neither added or multiplied each time to get the next term.
"Click here" to check the answer.
Identify each sequence. 25, 50, 75, 100, …
Arithmetic, d = 25
"Click here" to check the answer.
Identify each sequence. 2, 1, 0.5, 0.25
Geometric, r = ½ or 0.5
"Click here" to check the answer.
Stop! Go to Questions #6-11 about this section, then return to continue on to the next section.
Arithmetic Series
A series is an expression that indicates the sum of terms of a sequence. For example, if a1, a2, a3, ...an... is a sequence, then a1 + a2+ a3 +...an + ... is a series.
An arithmetic series is the indicated sum of the terms of an arithmetic sequence.
Consider the sequence 6, 9, 12, 15, 18…The sum of the first five terms of this sequence is denoted S5.
| S5 = 6 + 9 + 12 + 15 + 18 |
| S5 = 60 |
To develop a formula for the sum of the first n terms of a series, consider the series below.
 |
 |
 |
 |
 |
 |
Arithmetic Sequences and Series -- Amphitheater (03:08) Stop! Go to Questions #12-17 about this section, then return to continue on to the next section.
Geometric Series
A geometric series is the indicated sum of the terms of a geometric sequence. Consider the sequence 3, 9, 27, 81, … The sum of the first five terms, denoted S5 is:
 |
 |
 |
 |
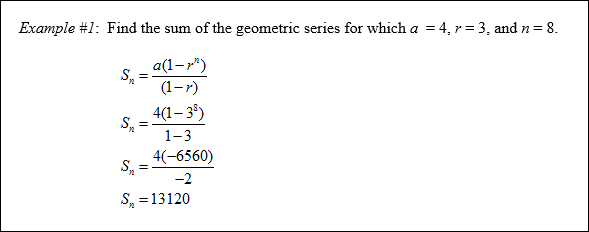Geometric Sequences and Series -- Family Tree (02:49)Stop! Go to Questions #18-22 about this section, then return to continue on to the next section.
Word Problems on Sequences and Series
Example#1: A culture of bacteria doubles every 3 hours. If there are 200 bacteria present at the beginning, how many bacteria will there be after 24 hours?
There are 25,600 bacteria present after 24 hours. |
Example#2: Counting your two parents, four grandparents, eight great grandparents etc. how many direct ancestors would you have if you could trace your family back for 10 generations?
Going back 10 generations, a person would have 2,046 direct ancestors. |
Example#3: Justin sells cars at a local dealership and earns $150.00 commission on the first car he sells each month. For each additional car Justin sells during the month, he receives $10.00 more on his commission. How much commission will Justin earn if he sells 16 cars?
Justin earns $3,600 for the month. |
. In this example, a16 is unknown.
Stop! Go to Questions #23-26 about this section, then return to continue on to the next section.
Binomial Theorem
Recall from algebra that a binomial is an expression of the form:
 |
In previous units, you have learned how to expand binomials where n = 2 or n = 3.
  |
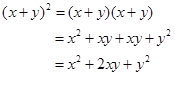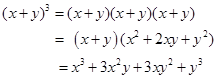However, expanding a binomial for large values of n would be quite time consuming. Fortunately, there is a theorem and a device that gives a pattern for expanding binomials for any value of n. The theorem is called the Binomial Theorem and the device applied to this theorem is called Pascal’s triangle.
Binomial Theorem: If n is a positive integer, then
Notice in this expression that the exponent on x decreases by one for each new term while the exponent on b increases by one for each new term.
Connected to the Binomial Theorem is the famous “Pascal’s Triangle”, which is given below and can be used to find the coefficients of a binomial expansion.
 |
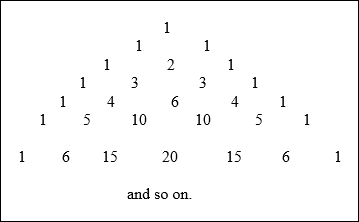Notice how the numbers in the row above determines the numbers in each row of the triangle. For example the number "2" in row #3 is the sum of 1 + 1 in row #2. The number "4" in row #5 is the sum of 1 + 3 or 3 + 1 in row #4 and so on. These numbers give the coefficients of an expanded binomial as the following examples show.
Example #1: Use Pascal’s Triangle to expand the following binomial.
|
Example #2: Use Pascal’s Triangle to expand the following binomial.
We will not apply the exponents to each term as it is obvious that very large numbers will result quite fast. For example the third term in the answer if expanded will be 37500a4b2. |
Stop! Go to Questions #27-34 to complete this unit.
