HYPERBOLAS AND SOLVING QUADRATIC SYSTEMS
 |
Unit Overview
In this unit you will learn how to write the standard equation of a hyperbola and solve systems of quadratic equations using substitution and elimination. You will also identify conic sections by examining their equations.
Hyperbola
A hyperbola is the set of points P(x, y) in a plane such that the absolute value of the difference between the distances from P to two fixed points F1 and F2 called foci, is a constant.
 |
 |
Let’s look at the properties of the hyperbola.
horizontal transverse |
vertical transverse | |
| (opens left and right like the figure above because the x variable is first) | (opens up and down because the y variable is first) | |
| The center of each hyperbola above is located at (h, k). | ||
Example #1: We can use the definition of hyperbola and the distance formula to find an equation for the hyperbola that contains P(x, y) and has foci at F1(–5, 0) and F2(5, 0) and has a constant difference of 6.
This hyperbola opens left and right and has a center at (0, 0). |
The equation of a hyperbola can be put into standard form the same way we put the equation of an ellipse in standard form, except we are subtracting. You need to remember how to complete the square.
Step #1: factor any coefficients that are not equal to 1 from the quadratic term and the linear term |
Step #2: take half of the linear term and square it |
Step #3: multiply the answer to step 2 by any number that was factored out and add this to the other side |
Example #2: Put this equation in standard form: 4y2 – 36x2– 72x + 8y = 176.
This hyperbola opens up and down and has a center at (–1, –1).
|
Stop! Go to Questions #1-8 about this section, then return to continue on to the next section.
Solving Quadratic Systems of Equations
To solve systems of quadratic equations, we can use substitution and elimination just like solving systems of linear equations.
A system of one quadratic equation and one linear equation can have two solutions, one solution or no solution.
Example #1: Solve the quadratic system of equations.
We can use substitution on this one because we know that y is equal to x + 1. Substitute x + 1 for y in the first equation.
The points where the graphs intersect represent the solutions of the system. |
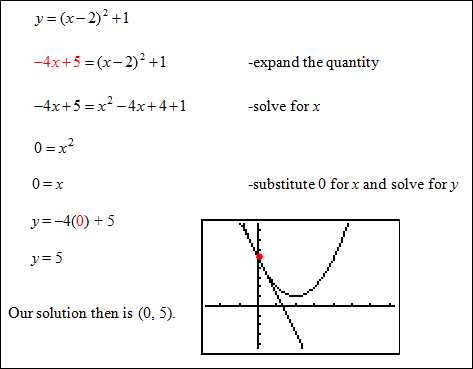
Example #2: Solve the quadratic system of equations.
We can use substitution on this because we know that y is equal to –4x + 5. Substitute –4x + 5 for y in the first equation.
|
Example #3: Solve the quadratic system of equations.
We can use substitution on this because we know that y is equal to x – 3. Substitute x – 3 for y in the first equation.
Since x2 – 4x + 5 does not factor, solve for x by using the quadratic formula.
Since x represents an imaginary number, this system of equations has no real solution. Note that the graph of this system of equations shows no points of intersection.
|
Example #4: Solve the system of equations:
We are going to use elimination because both variables are squared. Multiply the second equation by 2 so that we can eliminate the y2.
Add the two equations together so the y’s are eliminated.
Substitute +2 and –2 back into either of the equations for x and solve for y.
|
Stop! Go to Questions #9-13 about this section, then return to continue on to the next section.
Conic Sections
 |
Equations of Conic Sections |
A general equation for all conic sections is shown below.
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
*Notice that A is the coefficient of x2 and C is the coefficient of y2. |
Identify each of the following.
Example #1:
|
Example #2:
|
Example #3:
|
Example #4:
|
Stop! Go to Questions #14-30 to complete this unit.