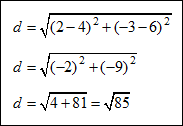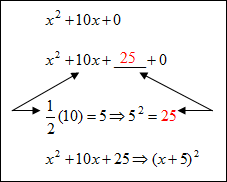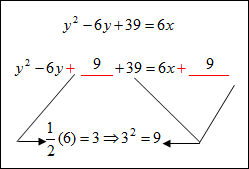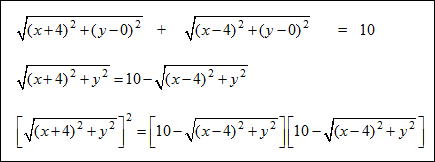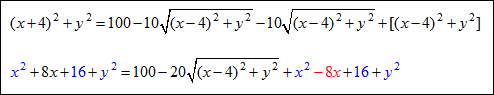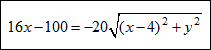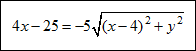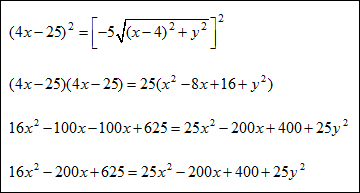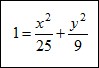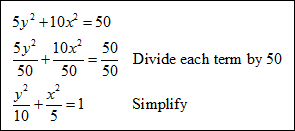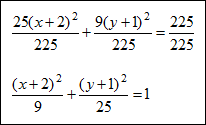PARABOLAS AND ELLIPSES
 |
Unit Overview
In this unit you will write equations for parabolas and ellipses given sufficient information. You will also examine graphs of parabolas and ellipses.
Parabola
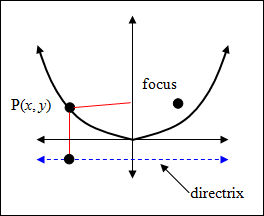
A parabola is a set of points P(x, y) in the plane whose distance to a fixed point, called the focus, equals its distance to a point on a fixed line, called the directrix.
 |
The standard equation of a parabola, also known as the vertex form, can be derived from this definition and will be done so in the next section. Below is an outline of equations of a parabola.
 |
Distance Formula |
The distance between two points (x1, y1) and (x2, y2) on a coordinate plane can be found using the following distance formula:
 |
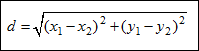Example #1: Find the distance between A(2, –3) and B(4, 6).
|
This formula can be used to find the equation of a parabola with a given focus and a given directrix.
Example #2: Find the equation of the parabola who has focus (5, 3) and directrix y = –1.
The equation of a parabola with focus (5, 3) and directrix y = –1 is  (x – 5)2 + 1. |
Completing the Square |
When given an equation of a parabola that is not in standard (vertex) form, it is necessary to put it in that form using a process called completing the square. This is a process by which you force a quadratic expression or equation to factor.
| 1.) Only work with the quadratic term (ax)2 and the linear term (bx) of the standard expression ax2 + bx + c. |
2.) Find  the linear term (bx), square it  , add this to the expression. |
Example #3: Complete the square for x2 + 10x + 0 to form a perfect square trinomial.
|
When working with an equation as opposed to an expression like above, you must keep it equal, meaning that when you add something to one side, you must do so to the other side. Follow the example below in which you complete the square to produce the vertex form of a parabola.
| Example #4: Write y2 – 6y + 39 = 6x in vertex form. Since this equation has only one squared term, we know it is a parabola. We want to complete the square using the terms associated with the variable y which means we will be solving the equation for x and it will be in the form x = a(y – k)2 + h.
The vertex form of y2 – 6y + 9 = 6x is  (y – 3)2 + 5 = x. The vertex is located at (5, 3), the axis of symmetry is y = 3, and the direction of opening is right.
|
Parabolas That Open Up or Down |
The standard form of a parabola that opens up or down is:
| y = a(x – h)2 + k |
If “a” is positive, the parabola opens up. |
If “a” is negative, the parabola opens down. |
| Example #1: Find the equation of a parabola with focus at (5, 3) and directrix y = –1. |
 |
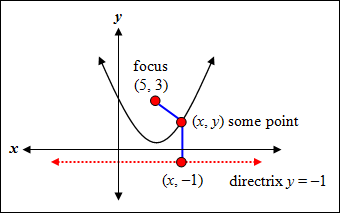| As stated in the definition of a parabola, the distance between the focus (5, 3) and a point on the parabola (x, y) is equal to the distance from the same point (x, y) and a point on the directrix (x, –1). Basically this is saying the blue lines have the same length. |
| Given: focus (5, 3) and directrix y = –1 distance between (x, y) and (5, 3) = distance between (x, y) and (x, –1)
-square both sides to eliminate the radicals
-Since there are two quantities that contain the variable y, we want to expand these quantities so we can solve the equation (expand these quantities by using the FOIL method).
-cancel out the y2 terms and solve for y
-divide all terms by 8
-This is the equation of our parabola in the example illustration. Notice that in the equation of a parabola that opens up or down the x term is squared, where the y term is not squared. |
Parabolas That Open Left or Right |
The standard form of a parabola that opens left or right is:
x = a(y – k)2 + h, where the vertex is located at (h, k) and the axis of symmetry is y = k. |
If “a” is positive, the parabola opens right. |
If “a” is negative, the parabola opens left. |
| Notice that in the equation of a parabola that opens left or right the y term is squared, where the x term is not squared. |
| Example #1: Given the equation 5x = y2 + 4y – 26, we are going to put it in standard form: |
| 1.) “complete the square” with the “y” terms, take half of 4 and square it, add this to both sides |
5x + 4 = (y2 + 4y + 4) – 26 |
| 2.) factor y2 + 4y + 4 into a perfect square |
5x + 4 = (y + 2)2 – 26 |
| 3.) subtract 4 from both sides |
5x = (y + 2)2 – 30 |
| 4.) divide everything by 5 to solve for x |
 |
| The vertex is located at (–6, –2) and the axis of symmetry is y = –2. The graph opens to the right since the y term is the squared term and the number in front of the squared term is positive. | ||
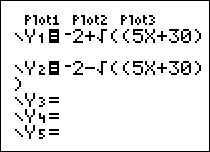
| To view the parabola on a graphing calculator, solve the equation for y. | ||
 |
||
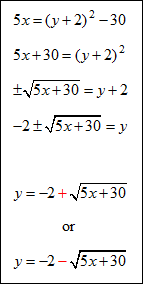| *Note: Due to the limitations of the graphing calculator, two equations must be entered to see the whole graph. | ||
|
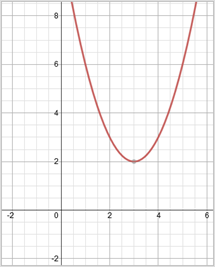
| Example #2: Write y = x2 – 6x + 11 in standard form. |
| 1.) “complete the square” with the “x” terms, take half of –6 and square it, add this to both sides |
y + 9 = (x2 – 6x + 9) + 11 |
| 2.) factor x2 – 6x + 9 into a perfect square. |
y + 9 = (x – 3)2 + 11 |
| 3.) subtract 9 from both sides |
y = (x – 3)2 + 11 |
| The vertex is located at (3, 2) and the axis of symmetry is x = 3. The graph opens up since the x term is squared and no number in front of the parentheses indicates it is a positive 1. |
| Since the equation is already solved for x, it can just be entered into the calculator as y = x2 – 6x + 11 or y = (x – 3)2 + 2. |
 |
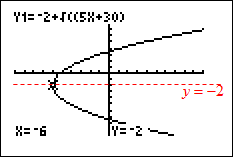
In the following questions, use the parabola with the equation x = 2(y – 3)2 – 7.
Name the vertex. x = 2(y – 3)2 – 7
The vertex of the parabola is (–7, 3).
The equation is in the form x = a(y – k)2 + h. The vertex is (h, k).
"Click here" to check the answer.
What direction does the parabola open? x = 2(y – 3)2 – 7
Right. Since the y term is squared, this parabola opens left or right.
Since a > 0, the parabola opens to the right.
"Click here" to check the answer.
Click on the graph to enlarge.
Name the axis of symmetry. x = 2(y – 3)2 – 7
y = 3. Since this parabola opens to the right, the axis of symmetry is a horizontal line that goes through the vertex. Therefore, the equation is in the form y = k.
"Click here" to check the answer.
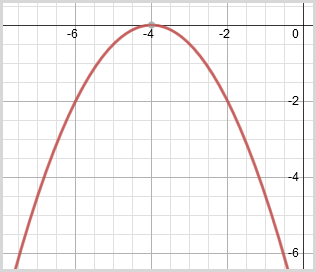
In the following questions, use the parabola with the equation 
.
Name the vertex.
The vertex of the parabola is (–4, 0).
The equation is in the form y = a(x – h)2 + k. The vertex is (h, k).
"Click here" to check the answer.
What direction does the parabola open?
Down. Since the x term is squared, this parabola opens up or down. Since a < 0, the parabola opens down.
"Click here" to check the answer.
Click on the graph to enlarge.
Name the axis of symmetry.
x = –4. Since this parabola opens to the down, the axis of symmetry is a vertical line that goes through the vertex. Therefore, the equation is in the form x = h.
"Click here" to check the answer.
Polynomial Functions Stop! Go to Questions #1-16 about this section, then return to continue on to the next section.
Ellipse
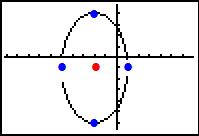
Ellipse: the set of all points P in a plane such that the sum of the distances from P to two fixed points F1 and F2 called the foci, is a constant.
 |
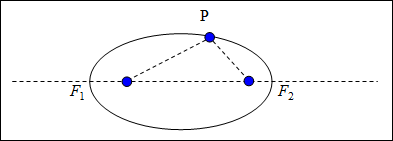*Note: Point P is represented at the top and the foci points, which are labeled, are the other two points.
The definition of ellipse is basically saying that:
| the distance | + |
the distance | = |
a given |
| between P and F1 | between P and F2 | constant |
 |
*An ellipse has two axes of symmetry
| major axis: the longer axis |
| minor axis: the shorter axis |
The length of the major and minor axes are 2a and 2b. The length of the major axis is the larger number of 2a or 2b.
We can write the equation of an ellipse given sufficient information just like we did with the parabola.
Example #1: Write the equation of an ellipse whose foci are F1(–4, 0) and F2(4, 0) and whose constant sum is 10. Use the definition of an ellipse to write the equation.
Given: F1(–4, 0) and F2(4, 0) and constant sum of 10 Represent Point P as (x, y).
Square both sides and FOIL the right side of the equation. Also expand any square quantities.
Isolate the radical. You will see that the x2 's, y2 's , and 16’s will cancel and you will add 8x to both sides.
To make this a little easier, we are going to divide both sides of the equation by 4 to reduce the large numbers.
Again we have to square both sides to eliminate the radical. Also make sure to expand the (x – 4)2 under the radical.
Move all variables to one side of the equation and all constant terms to the other side of the equation.
Divide everything by 225 so the equation is set equal to 1.
The center of this ellipse is located at (0, 0). To find the length of the major axis, take the square root of the larger number in the denominator and then double it. So the length of the major axis is 2(5) = 10. To find the length of the minor axis, take the square root of the smaller number in the denominator and then double it. So the length of the major axis is 2(3) = 6. |
To graph an ellipse:
 |
| -locate the center |
 |
| The center is (–2, 0). |
| -take the square root of the number in the denominator under the x variable (2), and from the center move this many units directly left and right. |
| -take the square root of the number in the denominator under the y variable (5) and from the center move this many units directly up and down. |
| -connect these points in an elliptical shape. |
 |
| The length of the minor axis is 2(2) or 4. |
| The length of the major axis is 2(5) or 10. |
Standard form of an ellipse:
| Example #1: Write 5y2 + 10x2 = 50 in standard form. The variables in the equation are both squared, therefore you do not need to complete the square. In the standard form of an ellipse, one side of the equation must be equal to 1, so divide each term be the constant.
 is the standard form for the equation.The center of the ellipse is (0, 0). The length of the major axis is 2  .The length of the minor axis is 2  . |
| Example #2: Write 25x2 + 9y2 + 100x + 18y = 116 in standard form. Then state the center and the length of the major and minor axes. Rewrite the terms so that the like variables are side by side.
Complete the square on both variables. Remember that before we can complete the square, our coefficients of the quadratic terms must equal one. Therefore you must factor a 25 out of the x terms and a 9 out of the y terms.
*Remember, if you have factored a number out of the terms to complete the square, you must put them back in when adding it to the other side. So the 100 on the right is from 25 times 4 and the 9 is from 9 times 1.
Divide all terms by 225 so the equation is equal to 1.
The center of this ellipse is located at (–2, –1). The length of the major axis is 2(5) or 10. The length of the minor axis is 2(3) or 6. If you were to graph this on a coordinate plane, you would move 3 units left and right of the center and 5 units up and down from the center and connect the points in an elliptical manner.
To graph the ellipse on a graphing calculator, solve the equation for y and then enter  . Use  5: ZSquare to get a true representation of the ellipse.
|
Stop! Go to Questions #17-33 to complete this unit.
