PDF

RATIONAL EXPRESSIONS AND GRAPHS


Unit Overview
In this unit you will work with rational expressions.  You will begin by looking at rational functions in the context of joint, inverse, and combined variation.  You will then take a functional approach to rational equations and explore the graph of such functions.


Inverse, Joint, and Combined Variation

In unit 2, you studied direct variation.  In this unit, you will review direct variation and study other types of variations.

Direct variation:  two variables, x and y, have a direct variation relationship if there is a nonzero number k such that y = kx or k = y/x, k is the constant of variation.  In a direct variation, as  one quantity increases, the other quantity increases or as one quantity decreases the other quantity decreases.  For example, an employee’s wages vary directly as the number of hours worked.  The more hours that the employee works the more money he makes.

Example #1:  The variable y varies directly as x, and y = 12 when x = 3.  Find x when y = 20.

a.)  Find the constant of variation by replacing x and y into y = kx and solve for k.

y = kx

12 = k(3)

4 = k

y = 4x


b.)  Find x when y = 20.

y = 4x
20 = 4x
x = 5

Example #2:  The length L that a spring will stretch varies directly with the weight W that is attached to the spring.  If a spring stretches 12 inches with 15 pounds attached, how far will it stretch with 20 pounds attached?

a.)  Write an equation to represent the direct variation.

L = kW


b.)  Find the constant of variation by replacing L and W and solve for k.

12 = k(15)
= k
= k
L = W

c.)  Find the length the spring stretches if 20 pounds are attached.  Find L when W is 20.

L = (20) = 16

The spring stretches 16 inches when 20 pounds are attached.

Inverse variation:  two variables, x and y, have inverse variation relationship if there is a nonzero number k, such that xy = k or y = , k is the constant of variation.  For two quantities with inverse variation, as one quantity increases, the other quantity decreases.  For example, rate and time for a fixed distance vary inversely with each other.  As your speed increases, the amount of time it takes to arrive at your destination decreases.  When you decrease your speed, the time it takes to arrive at your destination increases.

Example #3: The variable y varies inversely as x, and y = 22.5 when x is 6.2.

a.)  Find the constant of variation by replacing x and y into xy = k and solving for k.

xy = k

(6.2)(22.5) = k

139.5 = k
xy = 139.5 or y =

b.)  Find y when x is 0.1, 0.2 and 0.3.

xy = k xy = k xy = k
(0.1)y = 139.5 (0.2)y = 139.5 (0.3)y = 139.5
y = 1395 y = 697.5 y = 465

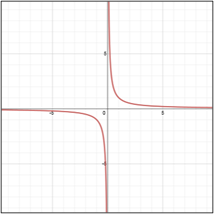
Look at the graphs below to see the location of each point on the graph of y = .

Example #4:  Twelve workers can complete a construction job in 8 days.  How many workers are needed to complete the same job in 6 days. 

This is an inverse variation, as the number of workers increases the number of days required decreases. 

a.)  Let x = the number of workers and y = number of days.  Find the constant of variation by replacing x and y into xy = k and solving for k.

xy = k

(12)(8) = k

96 = k
xy = 96

b.)  Find x when y is 6.

xy = 96
x(6) = 96
x = 12

Joint variation:  (one quantity varies directly as two or more quantities)  If y = kxz, then y varies jointly as x and z, and the constant of variation is k.

Example #5:   When y varies jointly as x and z, write the appropriate joint-variation equation, and find y for the given value of x and z.

y = –108 when x = –4 and z = 3, find y when x = 6 and z = –2

a.)  Find k.

–108 = (k)(–4)(3)

9 = k

b.)  Find the value of y by replacing the given values for x and z and the k with the constant found.

y = 9xz

y = 9(6)(–2)
y = –108

Example #6:   When y varies jointly as x and z, write the appropriate joint-variation equation, and find y for the given value of x and z.

y = 15 when x = 9 and z = 1.5; find y when x = 18 and z = 3

a.)  Find k.

15 = k(9)(1.5)

= k

b.)  Find the value of y by replacing the x and z with the given values and the k with the constant found.       

y = xz

y = (18)(3)
y = 60

Example #7:  The area (A) of a triangle varies jointly as the lengths of its base (b) and height (h).  If A = 133 when b = 19 and h = 14, find A when b = 11.5 and h = 7.

If A = 133 when b = 19 and h = 14, find A when b = 11.5 and h = 7.

a.)  Find the constant of variation and write the equation.

A = k(b)(h)
133 = k(19)(14)
133 = k(266)
= k
0.5 = k
A = 0.5(11.5)(7)

b.)  Find A when b = 11.5 and h = 7.

A = 0.5(11.5)(7)
A = 40.25

Combined variation:  when more than one type of variation occurs in the same equation,
z = .

Example #8:  z varies jointly as x and y and inversely as w.  If z = 3 when x = 3, y = –2 and
w = –4, find z when x = 6, y = 7, and w = –4.

a.)  Find k.

z =
3 =

–12 = –6k
2 = k

b.) Replace x, y and w with the given values and k with the constant found and solve for z.

z =
z =
z =     z = –21

For each of the following, state whether each equation represents a direct, joint, inverse or combined variation.  Then name the constant of variation.


question1Name the type of variation.  Name the constant of variation.  u = 8wz

The type of variation is "joint variation".

The constant of variation is 8.

"Click here" to check the answer.

question1Name the type of variation.  Name the constant of variation.  xy = 6.5

The type of variation is "inverse variation".

The constant of variation is 6.5.

"Click here" to check the answer.

question1Name the type of variation.  Name the constant of variation.  y = 10x

The type of variation is "direct variation".

The constant of variation is 10.

"Click here" to check the answer.



question1Name the type of variation.  Name the constant of variation.  y =

The type of variation is "inverse variation".

The constant of variation is 5/8.

"Click here" to check the answer.



question1Name the type of variation.  Name the constant of variation.  y =

The type of variation is "combined variation".

The constant of variation is 2/3.

"Click here" to check the answer.




question1Name the type of variation.  Name the constant of variation. 

The type of variation is "direct variation".

The constant of variation is 3/4.

"Click here" to check the answer.


Quicktime_Video_Icon  Direct and Inverse Variations -- Party Planning (03:42) 

Stop!  Go to Questions #1-13 about this section, then return to continue on to the next section.


Rational Functions and Their Graphs

Rational expression:  a rational expression is the quotient of two polynomials.

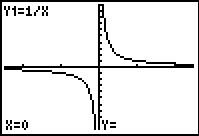  • The rational function f (x) = is undefined when x = 0 because this would make the denominator 0 and you can not divide by 0.  In general, the domain of a rational function is the set of all real numbers except those real numbers that make the denominator zero.
 
 
To find the domain:

1.)  Factor the denominator.
2.)  Use the zero product property to find values of x that = 0.
3.)  The values that you find in step 2 will be the values of x that are to be excluded from the solution.

Example #1:  Find the domain of .

1.)  Factor the denominator into (x – 12)(x + 3).
 
2.)  Set each of these factors equal to zero and solve.

x – 12 = 0 x + 3 = 0
   
x = 12   x = –3
 
3.)  The values of 12 and –3 will be the excluded values of the domain; therefore, the domain of the example would be all real numbers except 12 and –3 because these values would make the denominator = to zero and you can not divide by zero.

*Rational functions have asymptotes (a line that a curve approaches, but does not reach as its x or y values become very large or very small).  They may also have holes in the graph (places where the function is undefined at specific x-values.)
           
To find all vertical and horizontal asymptotes use the following rules:

Vertical asymptotes: if x – a is a factor of the denominator but not a factor of the numerator, then x = a is the equation of the vertical asymptote of the graph.
 
Horizontal asymptotes:  let R(x) = be a rational function.

*If the degree of P is less than the degree of Q, then y = 0 is the equation of the horizontal asymptote.

*If the degree of P equals the degree of Q and “a” and “b” are the leading coefficients, then y = is the equation of the horizontal asymptote.

*If the degree of P is greater than the degree of Q, then the graph has no horizontal asymptote.
 
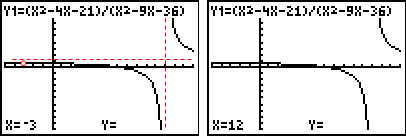
Hole in the graph:  if x – b is a factor of the numerator and the denominator, then there is a hole in the graph of the function at x = b.

Let’s look at  the  graph of the rational function given in Example #1, and then test our rules.

 
*Note:  Visually, holes do not show up very well on a graphing calculator.
 
 
a.)  (x – 12) is a factor of the denominator and not a factor of the numerator; thus, x = 12 is a vertical asymptote.
 
b.)  The degree of the numerator and the denominator are the same.  The leading coefficient in the numerator is 1 and the leading coefficient in the denominator is 1.  Thus, y = = 1.  The horizontal asymptote is y = 1.
 
c.)  Since (x + 3) is a factor of both the numerator and the denominator, there is a hole in the graph at x = –3.
 
Thus, for the rational function, , x = 12 is a vertical asymptote, y = 1 is a horizontal asymptote, and there is a hole in the function at x = –3. 

Example #2:  Identify all asymptotes and holes in the graph of the following.

R(x) =

Step #1:  Factor both the numerator and denominator.
 
Step #2:  Since (x – 2) and (x – 1) are not factors of the numerator (3x), the vertical asymptotes are x = 2 and x = 1.
 
Step #3:  Since the degree of the numerator is less than the degree of the denominator, the horizontal asymptote would be y = 0.
 
Step #4:  There are no holes in the graph because there are no common factors between the numerator and denominator.

Example #3:  Identify the domain restrictions and all asymptotes and holes in the graph of the following.
y =

Step #1:  Factor both the numerator and denominator.
 
y = =
 
Step #2:  Identify the domain restrictions and all asymptotes and holes.

domain restrictions:  x ≠ –2 or x ≠ –2 because both of these values would produce a zero in the denominator.
 
vertical asymptote:  x = –2 because (x + 2) is a factor of the denominator but not the numerator.
 
horizontal asymptote:  y = –1 because the degrees of the expressions are equal.
 
hole in the graph:  the graph has a hole at x = 1 because (x – 1) is a factor of both the numerator and denominator.

Let’s try one more.
Example #4:  Identify the domain restrictions and all asymptotes and holes in the graph of the following.
y =

Step #1:  Factor both the numerator and denominator.
 
y =
 
Step #2:  Identify the domain restrictions and all asymptotes and holes.

domain restrictions:  x ≠ –3 or x ≠ 1, again this is because those two values would produce a zero in the denominator.
 
vertical asymptote:  x = 1 because (x – 1) is a factor of the denominator but not the numerator.
 
horizontal asymptote:  none because the degree of the numerator is larger than the degree of the denominator.
 
hole in the graph:  there is a hole in the graph at x = –3 because (x + 3) is a factor of both the numerator and denominator.

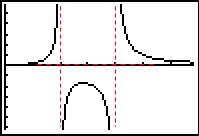
The following is the graph of a rational function with the asymptotes denoted by dashed lines.
y =
 

vertical asymptote x = 2

horizontal asymptote y = 1
 
         

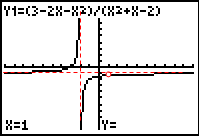
To graph this function by hand on paper, you can use your calculator as an aid. 

a.)  Enter the function into your calculator under Y=. 
 
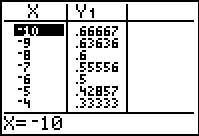
b.)  To find values to graph, you could use the TABLE feature, , and look at the x and y values. 

Note:  To reset your table, use TBLSET, ( ).  Move the cursor to TblStart and enter a number for x, something between –10 and 10, because this is about how wide your graph paper is.  Also, make sure that both “Indpnt:” and “Depend:” are set to “Auto”.


Remember that your graph will get very close to y = 1 and x = 2 but never touch it. 

 Rational Functions (03:15)

 Graphing Rational Functions (01:42)

 Graphing Rational Functions (Continued) (05:44)

 Reviews: Graphing Rational Functions (00:51)

 Asymptotes (An Introduction) (04:48)

 Finding Asymptotes (06:22)

Stop!  Go to Questions #14-30 to complete this unit.



Below are additional educational resources and activities for this unit.
 
Click on the icon to find and practice topics for this unit.
 
Graphing Simple Rational Functions
 
Graphing General Rational Functions