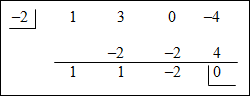Graphing and Solving Polynomial Equations

GRAPHING AND SOLVING POLYNOMIAL EQUATIONS

Unit Overview
In this unit you will graph polynomial functions and describe end behavior. You will solve polynomial equations by factoring and using a graph with synthetic division. You will also find the real zeros of polynomial functions and state the multiplicity of each. Finally, you will write a polynomial function given sufficient information about its zeros.

Graphs of Polynomial Functions

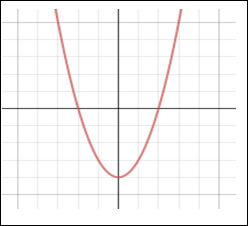
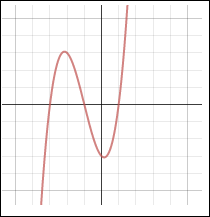
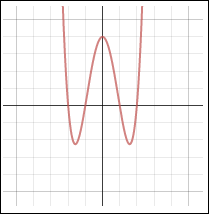
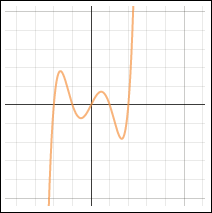
The degree of a polynomial function affects the shape of its graph. The graphs below show the general shapes of several polynomial functions. The graphs show the maximum number of times the graph of each type of polynomial may cross the x-axis. For example, a polynomial function of degree 4 may cross the x-axis a maximum of 4 times.

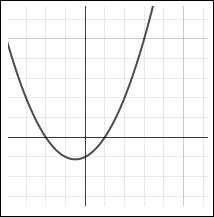
Linear Function Degree 1		Quadratic Function Degree 2


Cubic Function Degree 3		Quartic Function Degree 4


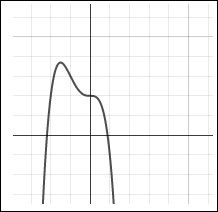
Quintic Function Degree 5

Notice the general shapes of the graphs of odd degree polynomial functions and even degree polynomial functions.

The degree and leading coefficient of a polynomial function affects the graph’s end behavior.

End behavior is the direction of the graph to the far left and to the far right.

The chart below summarizes the end behavior of a Polynomial Function.

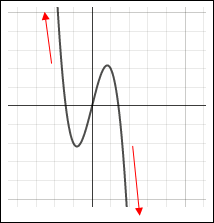
Example #1: Determine the end behavior of the graph of the polynomial function,
y = –2x³ + 4x.

The leading term is –2x³.

Since the degree is odd and the coefficient is negative, the end behavior is up to the far left and down to the far right.

Check by using a graphing calculator or click here to navigate to an online grapher.

y = –2x³ + 4x

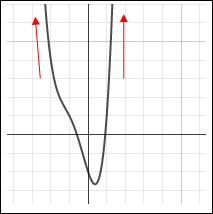
Example #2: Determine the end behavior of the graph of the polynomial function,
y = x⁴ + 3x³ + 2x²– 3x – 2.

The leading term is 1x⁴.

Since the degree is even and the coefficient is positive, the end behavior is up to the far left and up to the far right.

Check by using a graphing calculator or click here to navigate to an online grapher.

y = x⁴ + 3x³ + 2x²– 3x – 2

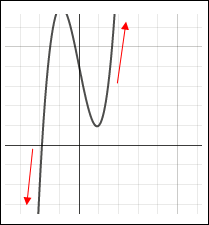
Example #3: Determine the end behavior of the graph of the polynomial function,
y = –5x + 4 + 2x³.

Rearrange the function so that the terms are in descending order.

y = 2x³ – 5x + 4

The leading term is 2x³.

Since the degree is odd and the coefficient is positive, the end behavior is down to the far left and up to the far right.

Check by using a graphing calculator or click here to navigate to an online grapher.

y = –5x + 4 + 2x³.

Now, let's practice determining the end behavior of the graphs of a polynomial.

Determine the end behavior of the graph of the polynomial function, y = –2x⁴+ 5x²– 3.

What is the degree of the function? y = –2x⁴+ 5x²– 3

The degree is 4.

"Click here" to check the answer.

What is the leading term? y = –2x⁴+ 5x²– 3

The leading term is –2x⁴.

"Click here" to check the answer.

What is the end behavior of the function?

Since the degree is even and the coefficient is negative,
the end behavior is down to the far left and down to the far right.

"Click here" to check the answer.

The real roots or zeros are the x-values of the coordinates where the polynomial crosses the x-axis.

By examining the graph of a polynomial function, the following can be determined:

if the graph represents an odd-degree or an even degree polynomial

if the leading coefficient if positive or negative

the number of real roots or zeros.

Example #4: For the graph, describe the end behavior, (a) determine if the leading coefficient is positive or negative and if the graph represents an odd or an even degree polynomial, and (b) state the number of real roots (zeros).

(a) The end behavior is up for both the far left and the far right; therefore this graph represents an even degree polynomial and the leading coefficient is positive.

(b) The graph crosses the x-axis in two points so the function has two real roots (zeros).

Example #5: For the graph, describe the end behavior, (a) determine if the leading coefficient is positive or negative and if the graph represents an odd or an even degree polynomial, and (b) state the number of real roots.

(a) The end behavior is down for both the far left and the far right. Therefore this graph represents an even degree polynomial and the leading coefficient is negative.

(b) The graph crosses the x-axis in two points so the function has two real roots (zeros).

Now, let's practice examining a graph and determining the characteristics of its equation.

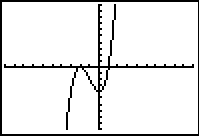
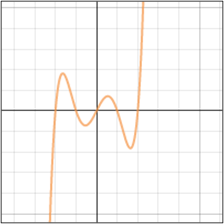
Examine this graph closely, and then answer the questions that follow about the equation of the graph.

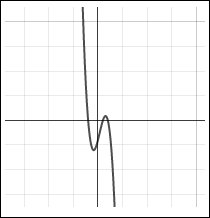Is the leading coefficient of the equation positive or negative and why?

Negative, because it is going up to the far left and down to the far right.

"Click here" to check the answer.

Does the polynomial have an odd or even degree?

Odd degree

"Click here" to check the answer.

How can the leading coefficient and the degree of the polynomial be determined by looking at the graph?

The end behavior of the graph is down for the far left and up for the far right.

"Click here" to check the answer.

The equation has how many real roots (zeros)?

The graph crosses the x-axis at three points, thus, the function has three real zeros.

"Click here" to check the answer.

Properties of Polynomial Graphs (10:42)

Stop! Go to Questions #1-16 about this section, then return to continue on to the next section.

Solving Polynomial Equations by Factoring

To solve a polynomial equation means to find the roots or zeros of the function.

To factor:

a) look for a GCF

b) look for a difference of squares a² – b²

c) use trial and error

Example #1: 5x³ – 12x² + 4x = 0

x(5x² – 12x + 4) = 0	GCF is x

x(5x – 2)(x – 4) = 0	Trial and Error

x = 0, 5x – 2 = 0, x – 4 = 0	Set each factor equal to zero and solve.

x = 0, x = , x = 2

This means that the polynomial 5x³ – 12x² + 4x = 0 has 3 real roots, 0,

, and 2. This is where the polynomial crosses the x-axis.

Example #2: x³ = 64x

x³ – 64x = 0	Set the equation equal to zero.

x(x² – 64) = 0	GCF is x.

x(x + 8)(x – 8) = 0	Factor using "difference of squares".

x = 0, x + 8 = 0, x – 8 = 0	Set each factor equal to zero and solve.

x = 0, x = –8, x = 8

This means that the polynomial x³ – 64x = 0 has 3 real roots, 0, –8, and 8.

Stop! Go to Questions #17-20 about this section, then return to continue on to the next section.

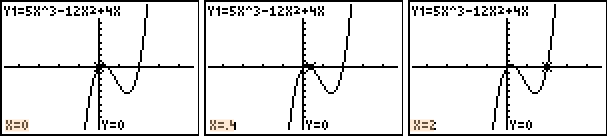
Solving Polynomial Equations by Using a Graph and Synthetic Division

To solve a polynomial function by graphing and using synthetic division:

1.) Graph the function on your calculator.

y = x³ + 3x²– 4

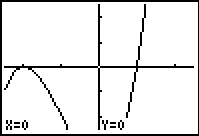
2.) Determine where the graph crosses the x-axis. In this case the graph looks like it touches the x-axis at (–2, 0). *Make sure you are viewing the standard viewing screen on your calculator, ZOOM 6. Then press ZOOM 2 ENTER to zoom in and get a better look.

Note: The above activity can be done using an online graphing program. Click here to navigate to the online grapher.

3.) Use synthetic division to test your choice. Make sure to insert a 0 to hold the place of the missing x term.
y = x³ + 3x²+ 0x – 4

4.) Since the remainder is 0, we now know that x + 2 is a factor x³ + 3x²– 4 = 0 and the other factor is x² + x – 2 (coefficients determined above). Write the polynomial in factored form, and then factor x² + x – 2.

x³ + 3x²– 4 = 0

(x + 2)(x² + x – 2) = 0	Factor completely.

(x + 2)(x + 2)(x –1)	Use the zero product property to solve.

x + 2 = 0 x + 2 = 0	x – 1 = 0

x = –2 x = –2	x = 1

Therefore the roots of this polynomial are 1 and –2, with –2 occurring twice.

Multiplicity of Roots

Multiplicity is the number of times a zero occurs in a function or the number of times a root occurs in an equation.

(x + 2)(x + 2)(x – 1) = 0 can be written as (x + 2)² (x – 1) = 0

*The root of 1 is called a “simple root” (or has a multiplicity of 1) and the root of –2 is a root of multiplicity 2. A root of multiplicity 2 is also called a double root.

Stop! Go to Questions #21-24 about this section, then return to continue on to the next section.

Writing a Polynomial Function

To write a polynomial function in standard form based on given information, use the following instructions.

Example #1: P(x) is of degree 2; P(0) = 12; zeros 2, 3

1.) Write the function in factored form using the given zeros

(x – 2)(x – 3)

2.) Because the graph of P can be stretched vertically by any nonzero constant factor and retain the same zeros, let “a” represent the stretch factor for this polynomial.

P(x) = a(x – 2)(x – 3)