LOGARITHMIC FUNCTIONS


Unit Overview
This unit is about the properties of exponential and logarithmic functions and solving equations using these properties.  Common logarithmic functions are used to solve exponential and logarithmic equations.  The change-of-base formula is used to evaluate exponential and logarithmic equations.  Applications of logarithmic functions include the pH scale in chemistry, sound intensity, the Richter scale for earthquakes, and Newton’s law of cooling. 

Note:  The picture shows San Francisco in 1906 after a devastating earthquake.


Logarithmic Functions

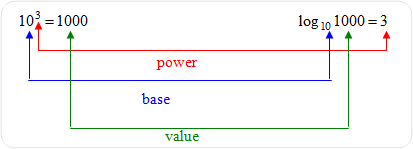
The logarithm of a number is the exponent to which a fixed value, called the base must be raised to produce that number.  For example, the log of 1000 to base 10 is 3 , because 1000 is 10 to the third power. 

exponential form
  
logarithmic form
base power = value
  
logbase value = power

In general, the logarithmic function is the inverse of the exponential function. 

 


A logarithm base b of a positive number x satisfies the following definition. 


Here is an animation that will help with understanding what a log is.


The expression, logb x, is read as “log base b of x.”  In other words, the logarithm y is the exponent to which b must be raised to get x.

*Because y = logb x  is the inverse of  y = bx and y = logb x is a function, the exponential function y = bx is a one-to-one function**.

**Meaning:  For each element in the domain (x-values), there is exactly one corresponding element in the range (y-values).

 


Example #1:  53 = 125 becomes log 5 125 = 3

More examples:  The black (dark) print represents what is given; the red (light) print represents the results. 


Stop!  Go to Questions #1-3 about this section, then return to continue on to the next section.


One-to-One Property of Exponents

 Let's examine how the One-to-One Property of  Exponents can help in solving logarithmic equations expressed in exponential form.

Here is an animation that will help with understanding the One-to-one property.


Example #1:  Solve  log 2 1 = r  for r. 

log 2 1 = r

-put in exponential form
2 r = 1 -ask yourself  “2 to what power is 1?”              
2 r = 2 0

-since 20 = 1, r = 0
r = 0  

Example #2:  Solve  log v 32 = 5 for v. 

log v 32 = 5

-put in exponential form
v5 = 32 -ask “Can 32 can be written using a base to the 5th power?”  
v5= 2 50

-the base 2 raised to the 5th power equals 32
v = 2 -since 25 = 32, v = 2

Example #3:  Solve  log b 9 = for b. 

log b 9 =

-put in exponential form
-multiply both exponents by 2

-Simplify the variable to the first power (b): 
                  
b1 = 9 2  
b = 81  


Let's practice evaluating a few logarithms by applying the One-to-One Property of Exponents.

question1Evaluate log 2 8 = x

x = 3 because 23 = 8

"Click here" to check the answer.

 

question1Evaluate log 9 9 = v

v = 1 because 91 = 9

"Click here" to check the answer.



question1Evaluate log 7 49 = q

q = 2 because 72 = 49

"Click here" to check the answer.



question1Evaluate log 2   = m

m = –2 because 5 –2 = 1/25

"Click here" to check the answer.


Stop!  Go to Questions #4-7 about this section, then return to continue on to the next section.


Graphs of Logarithmic Functions

To sketch the graph of a logarithmic function, use the fact that the logarithmic function is the inverse of the exponential function.

Remember that the inverse of a function is obtained by switching the x and y coordinates.  This reflects the graph about the line y = x. 

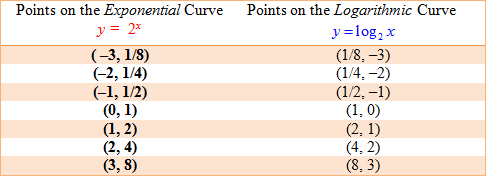
The table below shows how the x and y coordinates of the points on the exponential curve y = 2 x can be switched to find the coordinates of the points on the logarithmic curve y = log 2 x.


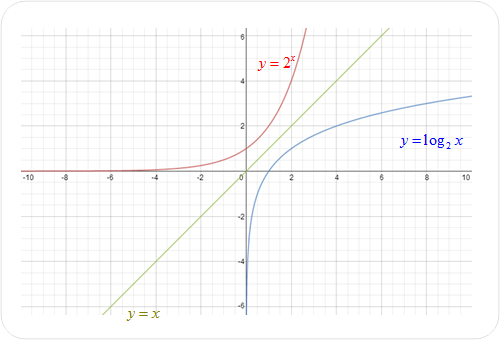Let's examine the logarithmic function closely.

Domain (x-coordinates) of a Logarithmic Function

Look at the left side of the logarithmic graph (blue).  Notice that the x‑coordinates of the points are very close to zero, but never equal zero or cross over the y-axis.  On the right side of the graph, the x-coordinates of the points grow infinitely.   

Thus, the domain for the logarithmic function is x > 0. 

Range (y-coordinates) of a Logarithmic Function

Since the y-coordinates of the points are unrestricted and can be infinitely small and infinitely larger, the range of a logarithmic function is all real numbers.

Features of a Logarithmic Function

-There is no y-intercept.
 
-The vertical asymptote is x = 0.

*Note: An asymptote is a line that a graph approaches as x or y increases in absolute value. 

-A logarithmic function has no horizontal asymptote.

-The x-intercept is 1. 

-The function is increasing over the domain.

*Note: If the base is between 0 and 1, the function decreases over the domain. 


 


Translating a Logarithmic Function

Knowing the shape of a logarithmic graph, it can then be shifted vertically and/or horizontally, stretched or compressed, and reflected.

The function logb x is the parent graph for the logarithmic function. 

When working with the logarithmic function, y = logb (x – h) + k, the graph of the parent function, y = logb x, can be translated horizontally by h units and vertically by k units. 

The a in the standard form of a logarithmic function y = a logb (x – h) + k results in a stretch (if |a| > 0), a compression
(if 0 < |a| <1 ) or a reflection (if a < 0).

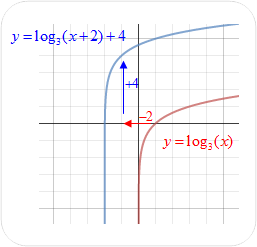
Example #1:  How does the graph of y = log3 (x + 2) + 4, compare to the graph of the parent function y = log3 x?  State the domain, range and identify the asymptote (the vertical line that the graph approaches).

y = a logb (x – h) + k

-standard form of a logarithmic function
y = log3 (x + 2) + 4 -given function
y = log3 (x – (–2) + 4 -rewrite the given function in standard form
h = –2 so the graph translates 2 units to the left
k = 4 so the graph translates 4 units up
The domain changes from x > 0 to x > –2.
The vertical asymptote is x = –2.
The range remains all real numbers.

The graph below shows the horizontal (–2) and vertical (+4) shifts. 


Example #2:  How does the graph of y = 3log4 (x) – 2, compare to the graph of the parent function y = log4 x?  State the domain, range and identify the asymptote (the vertical line that the graph approaches).

y = a logb (x – h) + k

-standard form of a logarithmic function
y = 3log4 (x) – 2 -given function
y = 3log4 (x – 0) + (–2) -rewrite the given function in standard form

a = 3 so the graph is stretched by a factor of 3
h = 0 so there is no horizontal shift

k = –2 so the graph shifts down 2 units
Because there is no horizontal shift, the domain remains x > 0, and thus, the vertical asymptote is  x = 0.

The range remains all real numbers.

The graph below compares the parent function (red) to a function that shows just the compression a = 3 (blue), and then the entire given function (green) which is compressed by 3 and shifted down two units. 

Stop!  Go to Questions #8-11 about this section, then return to continue on to the next section.


Properties of Logarithmic Functions

Logarithms, by definition, are exponents; thus, the properties of logarithms are similar to the properties of exponents.


Product Property:  The log of a product is equal to the sum of the log of the first base and the log of the second base.

Quotient Property:  The log of a quotient is equal to the difference of the logs of the numerator and denominator of the fraction that represents the division.

Example #1:  Rewrite the log expression as log5 2 + log5 6x as one log.



*Notice that the addition turned into multiplication.

Example #2:  Rewrite the log expression as log812 – log84 as one log.



*Notice that the subtraction turned into division.

Example #3:  Rewrite the log expression as logb4x – logb3y + logb y as one log.



*Notice that the subtraction turned into division and the addition turned into multiplication.


Power Property:  The logarithm of a power is equal to the power times the log of the base.

Example #4:  Evaluate:  log3 27 8

log3 27 8

= 8log3 27

Move the power in front of the log
  Multiply 8 times log3 27
= 8 ⋅ 3   Since 3 3 = 27, log3 27 is equal to 3.
= 24        



An exponential function and logarithmic function with the same base are inverses of each other.


Example #5:  Simplify:  + log5 25

Step #1:  since the bases are the same for the result is 4
4 + log5 25
Step #2:  25 needs to be written using a base of 5
4 + log5 52
Step #3:  Now that the bases are the same for log5 52 the result is 2
4 + 2 = 6

Therefore the value of  + log5 25 is 6.

Example #6:  Simplify:  log2 32 –

Step #1: rewrite 32 using a base of 2
log2 25 –
Step #2: since the bases are the same in the result is 3
log2 25 – 3
Step #3:  since the bases are the same in log2 25 the result is 5
5 – 3 = 2

Therefore the value of  log2 32 – is 2.





Here is an animation that will help with understanding the One-to-one Property of Logarithms.

If the bases of equivalent logarithms are the same, then the values are equal.

Example #7:  Solve for x:  log 2 (2x 2 + 8x – 11) = log 2 (2x + 9)

Step #1:  Since the bases are the same, we can set the expressions equal to each other and solve.

Step #2:  Both of these numbers are put back into the original logarithmic equation to check the solution.  If either number produces a negative logarithm, this answer must be excluded because the domain of logarithmic functions excludes negative numbers.

Check: (–5)

Since –5 results in a negative logarithm, it cannot be a solution.

Check: (2)

Since 2 results in a positive logarithm, then the solution to this problem is 2.


Stop!  Go to Questions #12-21 about this section, then return to continue on to the next section.


Applications of Common Logarithms

A common logarithm is a logarithm with base 10.  Common logarithms, log 10 x can be written simply as log x, without showing the 10.

To solve equations where x is an exponent:

Example #1:  Solve for x:  3x – 4 = 5x –1
log 3x – 4 = log 5x –1 1.)  tale the log of both sides
(x – 4) log 3 = (x – 1) log 5 2.)  use the power property to rewrite
x log 3 – 4 log 3 = x log 5 – log 5 3.)  distribute the x – 4 and the x – 1
x log 3 – x log 5 = 4 log 3 – log 5 4.)  combine like terms on one side (Put the x's on the left side and the constants on the right side.
x(log 3 – log 5) = 4 log 3 – log 5

5.)  on left, factor out the x
6.)  divide both sides by log 3 – log 5
x = –5.45        

7.)  use graphing calculator to solve*

 



*Use a graphing calculator (like TI-83 or TI-84) to solve logarithmic equations.  Make sure to  put parentheses around the entire numerator and the entire denominator when entering numerators or denominators.


The change-of-base formula works well with graphing calculators because the default base for logs on a calculator is 10.   The value of a log in a different base (b) can be found by taking the log of the value (x) and divide it by the log of the base (b).

Example #2:  Evaluate:  log 8 97

Example #3:  Evaluate:  log 7


*Use the graphing calculator to find the value of an expression using the change-of-base formula.

Logarithms and Earthquakes

The Richter scale is a logarithmic scale used to express the total amount of energy released by an earthquake.  Each number increase on the Richter scale indicates an intensity ten times stronger.  For example, an earthquake of magnitude 5 is ten times stronger than an earthquake of magnitude 4.  An earthquake of magnitude 6 is 10 × 10, or 100 times stronger.  In general, a measure of under 5 on the Richer scales is considered a minor earthquake, while a measure over 7 indicates major destruction. 
The formula, compares the intensity levels of earthquakes where I  is the intensity level determined by a seismograph, and M is the magnitude on the Richter scale. 


Example #4:  In 1906, an earthquake in San Francisco was estimated to have a magnitude of 7.8.  In 1989, an earthquake of magnitude 6.9 shook San Francisco.  How many times more intense was the 1906 earthquake than the 1989 earthquake?

Note:  The overview picture shows San Francisco in 1906 after the earthquake.


The 1906 San Francisco earthquake was 8 times more intense than the 1989 earthquake.

Stop!  Go to Questions #22-32 about this section, then return to continue on to the next section.


Solving an Exponential Equation with a Graph

A graphing calculator can also be used to solve exponential equations.

Example #1:   Solve 2x = 300 using a graphing calculator. 

 
Let Y1 = 2x

Let Y2 = 300

Adjust the window to find the point of intersection. 

The solution is x ≈ 8.23.

To determine the point of intersection, trace to the intersecting point or do the following: 

-On the graphing calculator, enter 2ND CALC 5: intersect.

-Press ENTER to accept the default for the First curve.  Press ENTER again to accept the default of the Second curve.  Press ENTER a third time and accept the calculator's Guess.  Press ENTER one final time to view the coordinates of the point of intersection.

The solution is x ≈ 8.23.  This is the x-coordinate of the point of intersection.

Use the questions below as a guide, if necessary, to set up the window on the graphing calculator.

question1What are reasonable domain values?

From Xmin = 0 to Xmax = 20

"Click here" to check the answer.


question1What are reasonable range values?

From Ymin = 0 to Ymax = 400

"Click here" to check the answer.




question1What are reasonable scale values?

From Xscl = 20 to Yscl = 20

"Click here" to check the answer.



Check the graph.

"Click here" to check the answer.

Stop!  Go to Questions #33-35 to complete this unit.