EXPONENTIAL GROWTH AND DECAY

In this unit, we will look at a variety of applications that are modeled by exponential functions. Exponential functions model many scientific phenomena. Some applications of exponential functions include population growth, compound interest, and radioactive decay. Radioactive decay is used to date ancient objects found at archeological sites.
Exponential Functions
Consider each of the following functions.
y = x2 |
y = 2x |
|
| This is a quadratic function because the base is a variable and the exponent is fixed. | This is an exponential function because the base is fixed and the exponent is a variable. |
An exponential function is a function with the general form y = abx, a ≠ 0, b is a positive real number and b ≠ 1. In an exponential function, the base b is a constant. The exponent x is the independent variable where the domain is the set of real numbers.
There are two types of exponential functions: exponential growth and exponential decay.
| In the function f (x) = bx when b > 1, the function represents exponential growth. |
| In the function f (x) = bx when 0 < b < 1, the function represents exponential decay. |
For example:
| a.) f (x) = 5x would represent exponential growth because b > 1. (b = 5) |
| b.) f (x) = 0.83x would represent exponential decay because 0 < b < 1. (b = 0.83) |
| c.) f (x) = 0.5(3)x would represent exponential growth because b > 1. (b = 3) |
| Example #1: Using a calculator and the exponential key (^), evaluate 4x for x = 0.5. Substitute the given value for x and evaluate.
|
|
| Example #2: Evaluate 5x for x = 4. Substitute the given value for x and evaluate.
|
| Example #3: Evaluate 10(2)x for x = 3. Substitute the given value for x and evaluate.
|
||
| Example #4: Evaluate 8(3)x − 1 for x = 5. Substitute the given value for x and evaluate.
|
Stop! Go to Questions #1-5 about this section, then return to continue on to the next section.
Graphing Exponential Functions
As with other functions, ordered pairs can be used to graph an exponential function. In this section we'll examine graphs that show exponential growth and exponential decay.
Graphing an Exponential Function with b > 1 |
The first example will show the graph of exponential growth because the base is greater than 1. (b = 2)
Example #1: Graph y = 2x.
|
The graphs of exponential functions showing growth have the following characteristics:
|
Graphing an Exponential Function with b < 1 |
The next example will show the graph of exponential decay because the base is a number between 0 and 1. (b = 1/2)
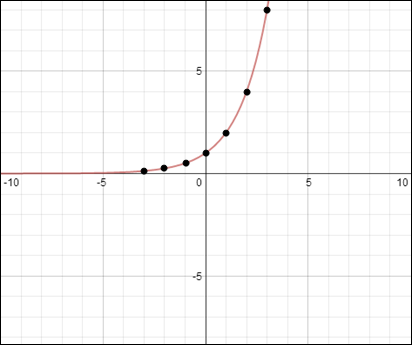
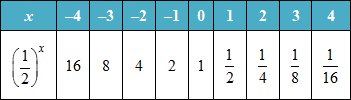
Example #2: Graph
|
The graphs of exponential functions showing decay have the following characteristics:
|
Graphing an Exponential Function with y = abx |
The factor a in y = abx can stretch or compress the graph of the parent graph y = bx. If a < 0, the graph will reflect across the x-axis.
The graphs of y = 2x (in blue) and y = 3(2)x (in red) are shown below. Each y-value of y = 3(2)x is 3 times the corresponding y-value of the parent function y = 2x.
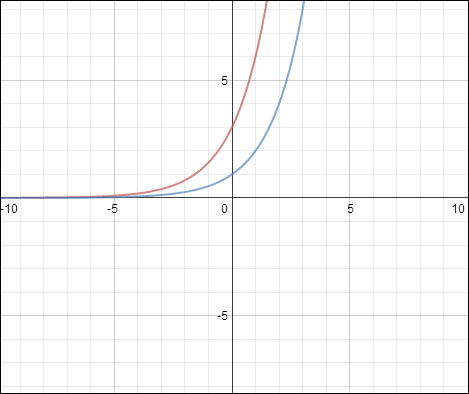 |
The graph of the parent function y = 2x is stretched by a factor of 3. Note the y-intercept of y = 3(2)x is 3. The domain of the function is the real numbers and the range is all positive numbers.
| Example #3: Compare the characteristics of the graphs of the given functions. The graphs of
In the graph, In the graph of |
Now, let's review the characteristics of exponential graphs.
![]() What is the domain of y = 4x ?
What is the domain of y = 4x ?
The real numbers.
"Click here" to check the answer.
*The domain of ALL exponent functions is the real numbers.
![]() What is the range of y = 3x ?
What is the range of y = 3x ?
The range is y > 0.
"Click here" to check the answer.
![]() What is the y-intercept of y = 2x ?
What is the y-intercept of y = 2x ?
The y-intercept is 1.
"Click here" to check the answer.
![]() What is the y-intercept of y =
What is the y-intercept of y = ![]() ?
?
The y-intercept is –1/3.
"Click here" to check the answer.
![]() What is the range of y =
What is the range of y = ![]() ?
?
The range is y < 0.
"Click here" to check the answer.
*The range is all negative numbers because the negative sign caused the graph to reflect over the x-axis.
Stop! Go to Questions #6-13 about this section, then return to continue on to the next section.
Applications of Exponential Growth and Decay
To solve exponential growth and decay problems, apply the rules given in the table.
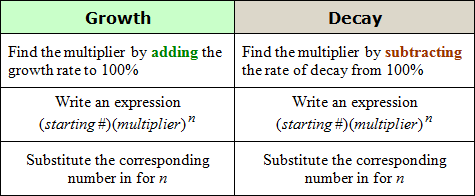 |
| Example #1: Find the multiplier for the rate of exponential growth, 4%. Since this represents exponential growth, add 100% + 4% = 104%. Express the percent as a decimal. 104% = 1.04 The multiplier is 1.04 Example #2: Find the multiplier for the rate of exponential decay, 9.3%. Since this represents exponential decay, subtract 100% – 9.3% = 90.7%. |
When a quantity grows by a fixed percent at regular intervals, the pattern can be represented by the following function.
 |
Now, let's see how these rules apply to some common real-world applications of growth and decay.
 Example #3: Suppose that you invested $1000 in a company’s stock at the end of the current year and that the value of the stock was predicted to increase at a rate of about 15% per year. Predict the value of the stock, to the nearest cent, at the end of the five years, and then ten years. Example #3: Suppose that you invested $1000 in a company’s stock at the end of the current year and that the value of the stock was predicted to increase at a rate of about 15% per year. Predict the value of the stock, to the nearest cent, at the end of the five years, and then ten years.At the end of the 5th year:
At the end of the 10th year:
|
 Example #4: Suppose that you buy a car for $15,000, and that its value decreases at a rate of about 8% per year. Predict the value of the car, to the nearest cent, after 4 years, and then after 7 years. Example #4: Suppose that you buy a car for $15,000, and that its value decreases at a rate of about 8% per year. Predict the value of the car, to the nearest cent, after 4 years, and then after 7 years.Value after 4 years:
Value after 7 years:
|
Doubling and Tripling |
The following example demonstrates exponential growth when the original amount is repeatedly multiplied by a positive number, called the growth factor.
The growth factor is determined by adding 100% and the rate of growth.
If an amount is doubled, this means that 100% is added to 100%, so the multiplier will become 200% or 2.
If an amount is tripled, then the multiplier will be 300% or 3.
Example #5: Thirty rabbits are introduced to a secluded area with no predators. Assume that the rabbit population doubles every six months. How many rabbits will be in the area after three (3) years?
|
![]() If the rabbit population tripled every 6 months, how many would be in the area after three years?
If the rabbit population tripled every 6 months, how many would be in the area after three years?
21,870 [y = 30(3)6]
"Click here" to check the answer.
Compound Interest |
Compound interest is modeled by an exponential function. |
 |
| A = the total amount of an investment P = principle r = annual interest rate n = number of times the interest is compounded per year t = time in years |
Example #6: Find the final amount of a $500 investment after 8 years at 7% interest compounded annually, quarterly, monthly and daily and compare the results.
Compounded Annually (The amount is compounded once a year, n = 1). |
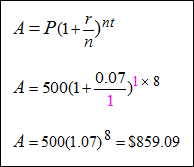 |
| Compounded Quarterly (The amount is compounded every 3 months in a year; that is, 4 times a year; thus, n = 4). |
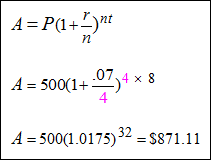 |
| Compounded Monthly (The amount is compounded every month in a year; that is, 12 times a year; thus, n = 12). |
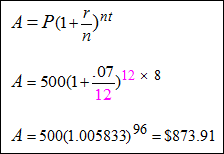 |
Compounded Daily (The amount is compounded every day in a year; that is, 365 times a year; thus, n = 365). |
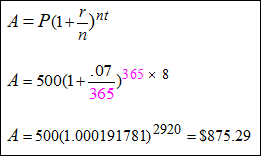 |
Summarizing the results in a table, we can make a quick comparison of the amounts. |
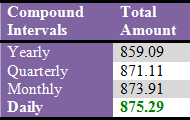 |
![]() Which type of compounding is most profitable?
Which type of compounding is most profitable?
Compounding Daily
"Click here" to check the answer.
Stop! Go to Questions #14-30 about this section, then return to continue on to the next section.
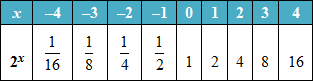
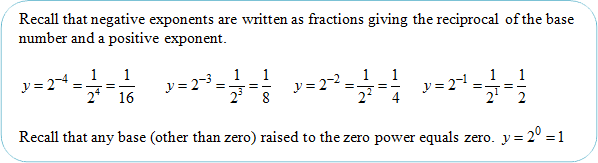

 a.) Since the population doubles twice a year, in 3 years it will have doubled 6 times. There are 6 time periods (3 years = 6 half years). (n = 6)
a.) Since the population doubles twice a year, in 3 years it will have doubled 6 times. There are 6 time periods (3 years = 6 half years). (n = 6)