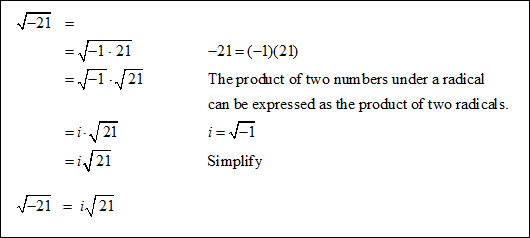Complex Numbers

PDF

COMPLEX NUMBERS


Unit Overview
Imaginary and complex numbers are introduced in this unit.  Complex numbers are extended to include the imaginary solutions of quadratic equations.  The operations of complex numbers are examined including rationalizing the denominator of fractions that have radicals in the denominator


The Discriminant

The discriminant of a quadratic equation gives an idea of the number of roots and the nature of the roots of an equation.  If ax2 + bx + c = 0 is the equation, then the discriminant of the equation is b2 − 4ac.

The discriminant can be seen in the quadratic formula.  The discriminant is the expression under the radical, b2 − 4ac.



Types of Solutions
*Imaginary solutions are numbers that involve the square root of a negative number.  The square root of a negative number is undefined in the "real" number system.  In the next section, we will extend the number system to include complex numbers which have imaginary parts.

Example #1: Find the discriminant and determine the number of solutions for each of the quadratics shown below.

1.)  3x2 − 6x + 4 = 0 2.)  4x2 − 20x + 25 = 0 *3.)  9x2 + 12x = −2
      b2 − 4ac       b2 − 4ac         b2 − 4ac
      (−6)2 − 4(3)(4)       (−20)2 − 4(4)(25)        (12)2 − 4(9)(2)
      36 − 48 = −12       400 − 400 = 0        144 − 72 = 72
      2 imaginary solutions       1 real solution        2 real solutions

*Note:  In the third quadratic equation, express the quadratic equation in standard form,
9x2 + 12x = 0, to determine a = 9, b = 12, and c = 2.

Quicktime_Video_Icon  The Quadratic Formula (06:38) 

Stop!  Go to Questions #1-3 about this section, then return to continue on to the next section.


Imaginary Numbers

In dealing with the quadratic formula, sometimes the discriminant is negative.  In this case, we can simplify the formula further if we know about imaginary and complex numbers. 

An imaginary number is a number in the form of ai where a is any real number and i 2 = −1; thus i = .


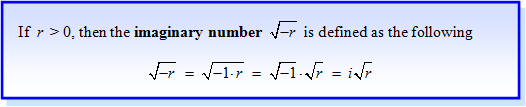When finding square root of a negative number, the first thing to do is factor out a (–1) which is equal to i.

Example #1:  Simplify: 


Quicktime_Video_Icon  Imaginary and Complex Numbers -- Electricity (04:35) 

Example #2:  Simplify: 


Example #3:  Simplify: 


Cyclic Powers of i

The powers of i are cyclic and repeat in a pattern of 4 numbers.  Thus, the powers of i have four possible outcomes.


If we continue the pattern, we have the following:

i 5 = i 4 ⋅ i = (1)i = i
 
i 6 = i 4 ⋅ i 2 = (1)(−1) = −1
 
i 7 = i 4 ⋅ i 3 = (1)(−i) = −i
 
i 8 = i 4 ⋅ i 4 = (1)(1) = 1

The table below is extended to show the cyclic pattern. 


Let's investigate this pattern further.

question1What are the values of i 9, i 10, i 11, and i 12 ?

i, –1, – i, and 1

"Click here" to check the answer.



question1When the powers of i equal one (i 4 = 1, i 8 = 1, i 12 = 1, and so on),
the exponents of i are multiples of what number?

Four

"Click here" to check the answer.



question1What is the value of i 99 ?

i 99 = i 96 * i 3 = 1 * – i = – i

"Click here" to check the answer.



Example #4:  i 26 = ?

i 26 = i 24 ⋅ i 2 Write the exponents as a product of exponents.
      = 1 ⋅ i 2 i 24 = 1 (The cyclic pattern shows that exponents of i that are multiples of 4 are equal to 1.)
      = 1 ⋅ (−1)

      = −1

i 2 = −1

 

i 26 = −1

Stop!  Go to Questions #4-9 about this section, then return to continue on to the next section.


Complex Numbers


*Two complex numbers are equal if the real parts are equal and the imaginary parts are equal.

Example #1:  Solve for “x” and “y”:  −3x + 4iy = 21 − 16i
real parts
imaginary parts
−3x = 21
4iy = −16i
     x = −7
y = −4

Thus x = –7 and y = –4

Quicktime_Video_Icon  Complex Numbers -- Electricity (03:15) 

Now let's look at how imaginary numbers are used in finding the solutions to some quadratic equations with solutions that are expressed as complex numbers.

Example #2:   Find the solution to the following quadratic:  x2 − 4x + 13 = 0.

Example #3:  Find the solution to the following quadratic:  6x2 − 3x + 1 = 0.

Stop!  Go to Questions #10-13 about this section, then return to continue on to the next section.


Computing with Complex Numbers


Adding and Subtracting Complex Numbers

To add or subtract complex numbers:
-combine the real parts
-combine the imaginary parts

Example #1:  Find the sum:  (−10 − 6i) + (8 − i)

 (−10 − 6i) + (8 − i)  
 −10 − 6i + (8 − i) Write without parenthesis.
 (−10 + 8) + (− 6i − i) Rearrange the real and imaginary parts.
−2 + −7i Combine the real and imaginary parts.
−2 −7i Simplify

Example #2:  Find the difference:  (−9 + 2i) − (3 − 4i)

(−9 + 2i) − (3 − 4i)  
−9 + 2i −3 + 4i Write without parenthesis. (Note  − −4i = +4i)
−9 − 3 + 2i + 4i Rearrange the real and imaginary parts.
−12 + 6i Combine the real and imaginary parts.


Multiplying Complex Numbers

Multiplying two complex numbers is accomplished in a manner similar to multiplying two binomials.  You can use the FOIL process of multiplication.

To multiply complex numbers in the form of a binomial times a binomial:
-use FOIL multiplication
-combine like terms
-change i 2 to (−1)

Example #3:  Find the product:  (2 − i)(−3 − 4i)

(2 − i)(−3 − 4i)  
−6 − 8i + 3i + 4i 2 FOIL
−6 − 8i + 3i + 4(−1) Express i 2 = −1
−6 − 5i − 4 Simplify
−10 − 5i Combine the real parts.

Example #4:  Find the product:  (8 − 3i)(−4 + 5i)

(8 − 3i)(−4 + 5i)  
−32 + 40i + 12i − 15i 2 FOIL
−32 + 40i + 12i − 15(−1) Express i 2 = −1
−32 + 52i + 15 Simplify
−17 + 52i Combine the real parts.

In the next example, an imaginary number is multiplied by a complex number by applying the distributive property.

Example #5:  Find the product:  5i(−7 −2i )

5i(−7 −2i )  
5i(−7) −5i(2i ) Distribute
−35i − 10i 2 Simplify
−35i − 10(−1) Express i 2 = −1
−35i + 10 Simplify
10 − 35i Apply the commutative property to express the complex number in proper form.

Stop!  Go to Questions #14-21 about this section, then return to continue on to the next section.


Conjugate of a Complex Number

In order to simplify a fraction containing complex numbers, you often need to use the conjugate of a complex number.  For example, the conjugate of 3 + 5i is 3 − 5i and the conjugate of 4 − 9i is 4 + 9i.


To simplify a quotient with an imaginary number in the denominator, multiply by a fraction equal to 1, using the conjugate of the denominator.  This is called rationalizing the denominator.

Example #1:  Rationalize the denominator for the given complex number.

Example #2:  Rationalize the denominator for the given complex number.

Stop!  Go to Questions #22-29 to complete this unit.



Below are additional educational resources and activities for this unit.
 
Click on the icon to find and practice topics for this unit.
 
Absolute Value of Complex Numbers
 
Operations with Complex Numbers