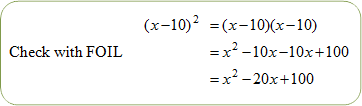PDF

SOLVING QUADRATIC EQUATIONS


Unit Overview
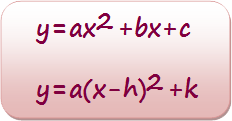
In this unit you will find solutions of quadratic equations by completing the square and using the quadratic formula.  You will also graph quadratic functions and rewrite quadratic functions in vertex forms.  Many connections between algebra and geometry are noted.


Completing the Square

When a quadratic equation does not contain a perfect square, you can create a perfect square in the equation by completing the square.  Completing the square is a process by which you can force a quadratic expression to factor.


Example #1:  Complete the given quadratic expression into a perfect square.

x2 − 20x

x2 − 20x + 100

(x − 10)2

(20) = 10, 102 = 100

Factor (Take square root of 100.)

The completed perfect square is x2 − 20x + 100 or (x − 10)2.

Example #2:  Complete the given quadratic expression into a perfect square.

x2 + 5x

x2 + 5x +







Factor (Take square root of 100.)

The completed perfect square is x2 + 5x + or .

Let's practice finding perfect square trinomials. 

question1What value of c will make the expression a perfect square trinomial?
x2 + 22x + c

c = 121 (1/2 of 22 = 11, and then 112 equals 121)

"Click here" to check the answer.



question1What value of c will make the expression a perfect square trinomial?
x2 − 18x + c

c = 81 (1/2 of –18 = –9, and then (–9)2 equals 81)

"Click here" to check the answer.



question1What value of c will make the expression a perfect square trinomial?
x2 + 11x + c

c = 121/4 (1/2 of 11 = 11/2, and then (11/2)2 equals 121/4)

"Click here" to check the answer.


Example #3:  Solve x2 + 6x = 16 for x by completing the square.

Quicktime_Video_Icon  Completing the Square Algebraically (03:56) 

Example # 4:  Solve x2 − 10x + 18 = 0 for x by completing the square.

*If the coefficient of the quadratic term is not 1, divide all terms by the coefficient to make it one.  Let's see how this works!

Example #5:  Solve 3x2 − 6x = 5 for x by completing the square.

Stop!  Go to Questions #1-8 about this section, then return to continue on to the next section.


 The Quadratic Formula


To use the quadratic formula
1.)  make sure the equation is in standard form
2.)  label the values of a, b, and c
3.)  replace the values into the equation and solve

Example #1:  Use the quadratic formula to solve the given quadratic for “x”.

Quicktime_Video_Icon  The Quadratic Formula (06:38) 

Example #2:  Use the quadratic formula to solve the given quadratic for “x”.


Example #3:  Use the quadratic formula to solve the given quadratic for “x”.


Stop!  Go to Questions #9-11 about this section, then return to continue on to the next section.


Graphing Quadratic Functions

The graph of a quadratic function is a parabola.  All parabolas are related to the graph of  f (x) = x2.  This makes f (x) = x2 the parent graph of the family of parabolas.  Any graph of a quadratic function is a transformation of the graph of  f (x) = x2.  These transformations are similar to the transformations studied in a previous, using the parent graph f (x) = ∣x∣.


Graphing a Quadratic Function of the Form  f (x) = ax2

Graph of the parent graph  f (x) = x2.
    

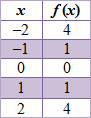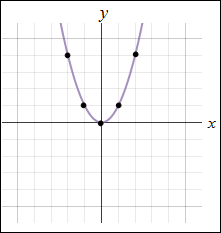In this graph, the vertex is (0, 0) and the axis of symmetry is x = 0.

Now, let's take a look at how the graph changes when a changes for  f (x) = ax2.
In y = , the graph is wider than the parent function, y = x2.  The vertex is (0, 0) and the axis of symmetry is x = 0.

In y = 3x2, the graph is more narrow than the parent function, y = x2.  

The vertex is (0, 0) and the axis of symmetry is x = 0.


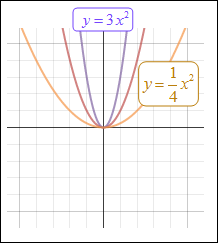If a is negative, then the graph is opens downward instead of upward.

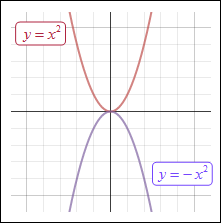In  f (x) = x2, the graph opens upward, and therefore has a minimum value.  The vertex is (0, 0) and the axis of symmetry is x = 0.

In  f (x) = −x2, the graph opens downward, and therefore has a maximum value.  The vertex is (0, 0) and the axis of symmetry
is x = 0.



Graphing a Quadratic Function of the Form  f (x) = x2

Vertical Translations

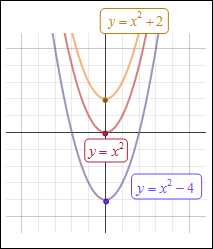In  f (x) = x2, the vertex is (0, 0) and the axis of symmetry is x = 0.

In  f (x) = x2, the vertex is (0, 2) and the axis of symmetry is x = 0.  The graph of  f (x) = x2 is translated up 2 units.

In  f (x) = x2 − 4, the vertex is (0, –4) and the axis of symmetry is x = 0.  The graph of  is translated down 4 units.
Horizontal Translations

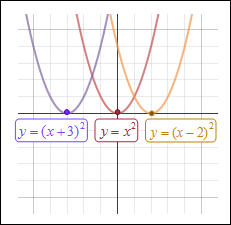In  f (x) = x2, the vertex is (0, 0) and the axis of symmetry is x = 0.

In  f (x) = (x − 2)2, the vertex is (2, 0) and the axis of symmetry is x = 2. The graph of  is translated right 2 units.

In  f (x) = (x + 3)2, the vertex is (–3, 0) and the axis of symmetry is x = –3.  The graph of  is translated left 3 units.

*Notice that it seems like the graph is sliding in the opposite direction as it should be translated; however, this will be explained in the discussion of the next two sections.
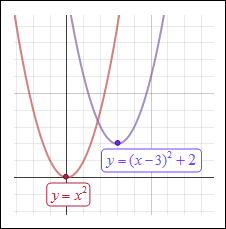Vertical and Horizontal Translation

In  f (x) = x2, the vertex is (0, 0) and the axis of symmetry is x = 0.

In  f (x) = (x − 3)2 + 2, the vertex is (3, 2) and the axis of symmetry is
x = 3. The graph of  f (x) = x2 is translated 3 units to the right and 2
units up.

Quicktime_Video_Icon  Factoring Quadratic Polynomials

Stop!  Go to Questions #12-16 about this section, then return to continue on to the next section.


Using Vertex Form

Expressing quadratic equations in vertex form can be very useful in determining how the equation relates to its graph.  It can be used to identify the vertex and y-intercept quickly along with other characteristics of its graph such as its maximum or minimum point and how wide or narrow it is.


The vertex is located at (h, k). 

The domain of quadratics is the real numbers. 

The range of quadratics is  when the vertex is a minimum and when the vertex is a maximum. 

The axis of symmetry is x = h.

The vertical stretch is a and can be used to determine if the parabola opens upward (when a is positive) or downward (when a is negative). 

Example #1:  State the vertex, the axis of symmetry, the maximum or minimum value, and the domain and the range for  f (x) = 4(x − 2)2 − 3.

 Compare the quadratic function with the general equation for vertex form and identify a, h, and k.

f (x) = a(x − h)2 + k

f (x) = 4(x − 2)2 − 3

f (x) = 4(x − 2)2 + −3           (–3 is the same as + –3)

a = 4, h = 2, k = –3
The vertex is (h, k) = (2, –3). 

The axis of symmetry is x = h or x = 2.
                       
Since a > 0, the parabola opens upward, and therefore the function has a minimum value.  The minimum value of is k, so the minimum value is –3.

Domain:  All real numbers.  (The domain for all quadratic functions is the real numbers.)

Range:  y ≥ –3 since the minimum value of the function is –3.  There is no value in the set of points for the parabola where the y-value is less than –3.


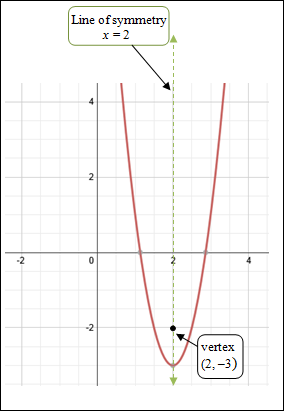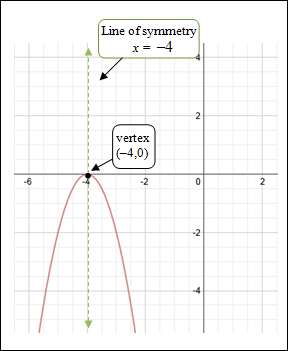
Example #2:  State the vertex, the axis of symmetry, the maximum or minimum value, and the domain and the range for  f (x) = −2(x +4)2.

 Compare the quadratic function with the general equation for vertex form and identify a, h, and k.

f (x) = a(x − h)2 + k

f (x) = −2(x +4)2

f (x) = −2(x − −4)2 + 0     (+4 is the same as  – –4, k = 0) 

a = –2, h = –4, k = 0

The vertex is (h, k) = (–4, 0). 

The axis of symmetry is x = h or x = –4.
                       
Since a < 0, the parabola opens downward, and therefore the function has a maximum value.  The maximum value of  f (x) is k, so the maximum value is 0.



Domain:  All real numbers.  (The domain for all quadratic functions is the real numbers.)

Range:  y ≤ 0 since the maximum value of the function is 0.  There is no value in the set of points for the parabola where the y-value is greater than 0.

Quicktime_Video_Icon  Finding the Maximum Value of a Quadratic Function (02:12) 

Let's practice identifying parts of a graph of a quadratic function when the function is expressed in vertex form. 

question1What is the vertex of the given quadratic function?
y = 2(x −3)2 + 4

The vertex is (3, 4).

"Click here" to check the answer.


question1Is the vertex of the function a maximum or minimum point?  Explain why?
y = 2(x −3)2 + 4

The vertex is a minimum point because a (2) is positive.

"Click here" to check the answer.


question1What is the vertex of the given quadratic function?
y = −4(x + 5)2 + 2

The vertex is (–5, 2).

"Click here" to check the answer.


question1Is the vertex of the function a maximum or minimum point? Explain why?
y = −4(x + 5)2 + 2

The vertex is a maximum point because a (–4) is negative

"Click here" to check the answer.


question1What is the axis of symmetry of the graph for the given quadratic function?
y = −(x + 1)2 + 2

The axis of symmetry is x = –1.

"Click here" to check the answer.


question1What is the axis of symmetry of the graph for the given quadratic function?
y = −5(x − 4)2 + 2

The axis of symmetry is x = 4.

"Click here" to check the answer.



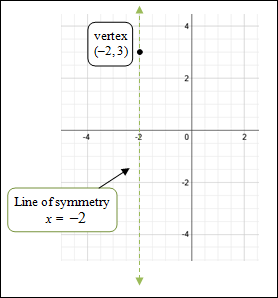
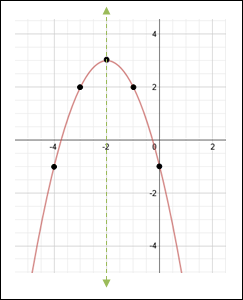
Example #3:  Graph  f (x) = −(x +2)2 + 3.

Identify the constants for this graph:

f (x) = a(x − h)2 + k

f (x) = −(x +2)2 + 3

f (x) = −1(x − −2)2 + 3     (a is understood to be –1, +2 = – –2)

a = –1, h = –2, k = 3

Since a < –1, the parabola opens downward.

Plot the vertex (h, k) = (–2, 3) and draw the axis of symmetry x = –2.


Plot two points:  Let x = –1 since it is near the line of symmetry.

f (x) = −(x + 2)2 + 3

f (−1) = −(−1 + 2)2 + 3

            = −(1)2 + 3     

           = −1 + 3

           = 2

Plot (–1, 2) and the
symmetric point (–3, 2).

Plot two additional points:

f (x) = −(x + 2)2 + 3

f (−1) = −(0 + 2)2 + 3

            = −(2)2 + 3     

           = −4 + 3

           = −1

Plot (0, –1, ) and the
symmetric point (–4, –1).

Sketch the curve. 

Locating the vertex first proved very useful in deciding which additional points to graph.  The line of symmetry helped in determining the symmetrical points which occur in parabolas. 

Stop!  Go to Questions #17-22 about this section, then return to continue on to the next section.


Write Quadratic Functions in Vertex Form

To write a quadratic function in vertex form, complete the square first, using the quadratic and linear terms only, if the coefficient of the quadratic term is 1.


Example #1:  Write the given quadratic function in vertex form, and then state the coordinates of the function’s vertex and the axis of symmetry.

g (x) = x2 + 6x + 5 Notice that g (x) = x2 + 6x + 5 is not a perfect square.
   
g (x) = (x2 + 6x +9) + 5 −9 Complete the square by taking half of the linear term (6) which is 3, and square it to get 9.  Balance this addition by subtracting 9.
   

g (x) = (x + 3)2 − 4

 Factor x2 + 6x + 9 into (x + 3)2and combine +5 – 9 = –4.

The vertex form of the given quadratic functions is g (x) = (x + 3)2 − 4.

f (x) = a(x − h)2 + k  
g (x) = (x − −3)2 + −4

(+3 = – –3,   –4 = +–4)

The vertex of this quadratic function is located at (–3, –4) and the axis of symmetry is x = –3.

*If the leading coefficient (a) is not one, factor the coefficient (a) out of the quadratic and linear terms only and adjust to keep the equation in balance.

Example #2:  Write the given quadratic function in vertex form, and then state the coordinates of the function’s vertex and the axis of symmetry.

f (x) = 2x2 + 12x + 13  
   
f (x) = 2(x2 + 6x) + 13 Group the quadratic and linear terms only, 2x2 + 12x, and factor, dividing by 2.  Factor a 2 out of the quadratic and linear terms.          
   
f (x) = 2(x2 + 6x +9) + 13 −18 Complete the square inside the parentheses and keep the equation in balance.
   
This is a little different because when you take one-half of 6 and then square it you get 9, but the parentheses are multiplied by 2, so you are really adding 18 so to balance this addition you must subtract 18.
   
f (x) = 2(x + 3)2 − 5 Factor x2 + 6x + 9 into (x + 3)2 and combine +13 – 18 = –5.

The vertex form of the given quadratic functions is f (x) = 2(x + 3)2 − 5.

f (x) = a(x − h)2 + k  
g (x) = 2(x − −3)2 + −5

(+3 = – –3,   –5 = +–5)

The vertex of this quadratic function is located at (–3, –5) and the axis of symmetry is x = –3. 

*If a quadratic function is in standard form, ax2 + bx + c = y, then it is possible to locate the axis of symmetry by using the following formula:


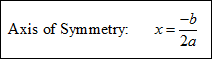Example #3:  Find the axis of symmetry for the given quadratic function.

f (x) = 2x2 + 18x + 19

a = 2, b = 8, c = 19
   
 The axis of symmetry is x = .


The axis of symmetry is  x = –2.

The axis of symmetry also refers to the x-value of the vertex. 

To find the y-value of the vertex:
1.)  Replace the value of x into the equation
2.)  Solve for y

Example #4:  Find the vertex of the parabola for the quadratic function, y = 2x − 2 + x2.
y = 2x − 2 + x2  
   
y = x2 + 2x − 2 Put in standard form.
   
a = 1,   b = 2,   c = –2

Identify a, b, and c.
   
Find the axis of symmetry.    
   
The axis of symmetry is x = –1.

 

  

y = (−1)2 + 2(−1) − 2
y = 1− 2 − 2
y = −3

Replace all x values with –1 and solve for y.
 
Therefore, the vertex of this parabola is located at (–1, –3).

Stop!  Go to Questions #23-30 to complete this unit.