QUADRATIC FUNCTIONS


Unit Overview
Quadratic functions have important applications in science, engineering, and entertainment.  For example, fireworks, when fired, follow a parabolic path and many explode when the vertex is reached.  This unit will introduce you to quadratic functions.  In addition, you will solve quadratic equations using factoring and the Zero Product Property.  Lastly, you will explore many real-world applications of the quadratic functions and their parabolas.

Introduction to Quadratic Functions

Quadratic functions have the form f (x) = ax2 + bx + c where the highest exponent is 2.

ax2 is the quadratic term

bx is the linear term

c is the constant term

Are the following functions, quadratic functions?

f (x) = 7x2 − 3x + 4

g (x) = 3x2 − 5

h (x) = 4x3 − 2x2+ x + 8

j (x) = 6x + 7

yes, the highest exponent is 2

yes, the highest exponent is 2

no, the highest exponent is 3

no, the highest exponent is 1

parabola:  the graph of a quadratic function


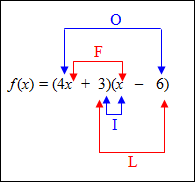
axis of symmetry:  a line that divides the parabola into two parts that are mirror images of each other.

vertex:  either the lowest point on the graph or the highest point on the graph.

domain of any quadratic function:  the set of all real numbers.

range:  all real numbers ≥ the minimum value of the function (when opening up) or all real numbers ≤ the maximum value of the function (when opening down).

If given a function, such as f (x) = (4x + 3)(x – 6), and asked to express it into quadratic form, use FOIL (First Outer Inner Last) multiplication to write it in the form
y = ax2 + bx + c.

Example #1:  Express f (x) = (4x  +  3)(x   –   6) in quadratic form using the FOIL method.


Multiply the First terms, the Outer terms, the Inner terms, and the Last terms and add them.

      F               O              I             L
(4x ⋅  x) + (4x ⋅ –6) + (3 ⋅ x) + (3 ⋅ –6)

      4x2– 24x + 3x – 18                 -combine like terms
            4x2–21x – 18

Therefore, the quadratic form is y = 4x2–21x – 18.

Quicktime_Video_Icon  Multiplying Binomials (FOIL) (03:22)

The general form for a quadratic function is y = ax2 + bx + c.

Thus, a = 4,     b = –21,     and  c = –18.


By examining “a” in f (x) = ax2 + bx + c, it can be determined whether the function has a maximum value (opens up) or a minimum value (opens down).


Example #2:  Determine if vertex of the quadratic function is a minimum or a maximum point in its parabola and if the parabola opens upward or downward.

a.)   f (x)= –5x + 2x2 + 2        b.)  g (x) = 7 – 6x – 2x2

*put the equations in descending order (largest exponent first)

f (x)= 2x2 – 5x + 2     g (x)= –2x2 – 6x+ 7
    
Since “a” is positive (2), this means that the graph opens up and has a minimum at the vertex.

       
Since “a” is negative (–2), this means that the graph opens down and has a maximum at the vertex.

Quicktime_Video_Icon  Graphs of Quadratics (03:54) 

Let's practice:

question1For the given function, state whether the parabola opens up or down and why.
f (x) = –3x2 – 4x + 5    

The parabola opens DOWN because "a" is negative (–3).

"Click here" to check the answer.



question1Is the vertex of the parabola of this quadratic function a maximum or a minimum point?
f (x) = –3x2 – 4x + 5  

Since the parabola opens downward, the vertex will be at a MAXIMUM point.

"Click here" to check the answer.


question1For the given function, state whether the parabola opens up or down and why.  
(Hint:  Put the equation in descending order first.)

f (x) = –3 + 2x + x2

The parabola opens UP because "a" is positive (1).

"Click here" to check the answer.



*Note:  When there is no number in front of a variable, it is "understood" to be one. 
Thus, in this last example, we think of x2 as 1x2.

question1Is the vertex of the parabola of this quadratic function a maximum or a minimum point?
f (x) = –3 + 2x + x2   

Since the parabola opens upward, the vertex will be at a MINIMUM point.

"Click here" to check the answer.

Stop!  Go to Questions #1-10 about this section, then return to continue on to the next section.

Solving Quadratic Equations by Graphing

One method that can be used for solving quadratic equations is graphing.  The solutions of a quadratic equation are called the roots of the equation.  The roots of a quadratic equation can be found by finding the x-intercepts or zeros of the quadratic function.  A quadratic equation can have two real roots, one real root or no real roots.  Real roots are numbers that are in the "real number system". 
roots of an equation:  Roots are the solutions of a quadratic equation and can be called the zeros of the quadratic function.


Two Real Roots

Let's graph a quadratic that has TWO real roots as a solution.
Example #1:  Solve x2 − 6x + 8 = 0

First, write the equation as the related function:  f (x) = x2 − 6x + 8.

 *Note:  In the related function, just change zero to f (x). 

Next, graph the function.

To graph this function, it becomes easier to find points for the graph if we know where the vertex is located.  The x-coordinate of the vertex can be found by using the following formula:

In the function f (x) = x2 − 6x + 8, a = 1 and b = –6.

Thus, .

Now, find the y-coordinate of the function by substituting 3 into the original function.

y = x2 − 6x + 8
y = (3)2 − 6(3) + 8
y = 9 − 18 + 8
y = −1

We now know the vertex of the parabola is (3, –1).

Next, make a table of values, choosing x-values arbitrarily that give points on both sides of the vertex of the parabola.

In the table of values for this function ,use x-values around x = 3, and substituting them into the original function to find the corresponding y-values; then graph each point.

    

From the table and the graph, the zeros (roots) of the function are clearly displayed.  The zeros are 2 and 4. 

Therefore, the solutions of the equation are x = 2 and x = 4.


One Real Root

Now, let's examine the graph of a quadratic that has ONE real root as a solution.

Example #2:  Solve x2 + 4x + 4 = 0 by graphing.

First, write the equation as the related function:  f (x) = x2 + 4x + 4

Next, graph the function.

To graph this function, it becomes easier to find points for the graph if we know where the vertex is located.   The x-coordinate of the vertex can be found by using the following formula:

In the function  f (x) = x2 + 4x + 4, a = 1 and b = 4.

Thus,

Now, find the y-coordinate of the function by substituting –2 into the original function.

y = x2 + 4x + 4
y = (−2)2 + 4(−2) + 4
y = 4 − 8 + 4
y = 0

We now know the vertex of the parabola is (–2, 0).

Next, we'll make a table of values, choosing x-values arbitrarily that give us points on both sides of the vertex of the parabola.

Make a table of values for this function using x-values around x = –2 and substituting them into the original function to find the corresponding y-values; then graph each point.

    

From the table and the graph, the zero (root) of the function is clearly displayed.

The graph has only one x-intercept at –2; thus, the zero is –2. 

Therefore, the one solution of the equation is x = –2.


No Real Roots

Finally, let's examine the graph of a quadratic that has NO real roots.

Example #3:  Solve x2 − 4x + 5 = 0 by graphing.

First, write the equation as the related function:  f (x) = x2 − 4x + 5

Next, graph the function.

Find the vertex point using .

In the function  f (x) = x2 − 4x + 5, a = 1 and b = –4.

Thus, .

Now, find the y-coordinate of the function by substituting 2 into the original function.

y = x2 − 4x + 5
y = (2)2 − 4(2) + 5
y = 4 − 8 + 5
y = 1

We now know the vertex of the parabola is (2, 1).

Make a table of values for the function using x-values around x = 2 and substituting them into the original function to find the corresponding y-values; then graph each point.

    

The graph has no x-intercepts.  This means that the equation has no real solutions.

Quicktime_Video_Icon  The Number of Possible Solutions (01:01) 


Estimate Roots

Sometimes exact roots for a quadratic equation cannot be found.  Instead, an estimate can be made by stating the consecutive integers between which the roots are located.

Example #4:  Solve  −x2 + 4x − 1 = 0 by graphing.

First, write the equation as the related function:  f (x) = −x2 + 4x − 1.

Next, graph the function.

Find the vertex point using .

In the function f (x) = −x2 + 4x − 1, a = –1 and b = 4.

Thus, .

Now, find the y-coordinate of the function by substituting 2 into the original function.

y = −x2 + 4x − 1
y = −(2)2 − 4(2) − 1
y = −4 + 8 − 1
y = 3

We now know the vertex of the parabola is (2, 3).

Make a table of values for the function using x-values around x = 2 and substituting them into the original function to find the corresponding y-values; then graph each point.

    

The x-intercepts of the graph are between 0 and 1 and between 3 and 4.  So, one solution is between 0 and 1, and the other is between 3 and 4. 

*Notice in the table that the value of the function changes from positive to negative between the x-values of 0 and 1 and between the x-values of 3 and 4. 


question1The equation and its related graph are shown.  What are the solutions (real roots) for the equation?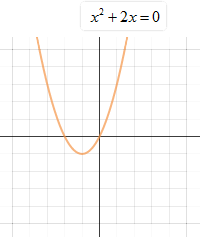

The solutions are x = 0 and x = –2.

"Click here" to check the answer.



question1The equation and its related graph are shown.  What are the solutions (real roots) for the equation?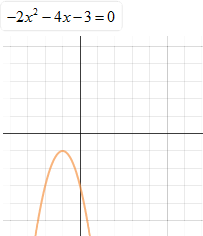

There are no real roots for this equation.

"Click here" to check the answer.



question1The equation and its related graph are shown.  What are the solutions (real roots) for the equation?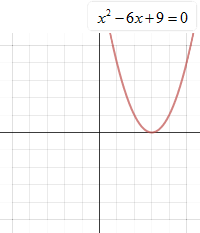

The solution is x = 3.

"Click here" to check the answer.



question1The equation and its related graph are shown.  What are the solutions (real roots) for the equation?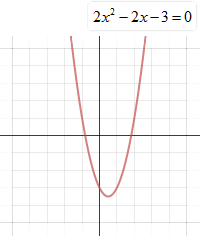

The solutions are between –1 and 0 and between 1 and 2.

"Click here" to check the answer.

Stop!  Go to Questions #11-15 about this section, then return to continue on to the next section.

Solving Quadratic Equations

Quadratic equations that contain a perfect square can be solved by finding the square roots. 

To solve quadratic equations using this method:
          1.)  isolate the quadratic term
          2.)  find the square root of each side

Stop!  Go to Questions #16-19 about this section, then return to continue on to the next section.


 Factoring Quadratic Expressions

Factoring reverses the process of multiplying two expressions.

A.  Two terms
     -look for a greatest common factor

B.  Three terms (leading coefficient = 1 or –1)
     -Look for a greatest common factor, then:

-find two factors of the constant term, that when added together, result in the middle term.

*if the last term is positive, then both factors will have the same sign, that sign will be the sign of the middle term.

*if the last term is negative, then one factor is positive and the other is negative.

*If the leading coefficient is negative, factor out a –1 first, then proceed to find factors of the last term that add up to the middle term.


C.  Difference of Squares (two terms)
     -the first term will be a perfect square
     -the last term will be a perfect square
     -the terms will be separated with a subtraction sign

     -look for a GCF
     -factor using the following process

D.  Three terms (leading coefficient > 1) Trial and Error
     -factor the first term
     -factor the constant term
     -the sum of the outside product and inside product must equal the middle term

*The combination of (5x + 4)(x + 2) works because the product of the outside terms 10x and the product of the inside terms 4x will result in the middle term 14x.

*If this had not worked, the 1 and 8 would have been used  to try to determine a combination that gave the correct product sum.

Again this is called Trial and Error, so there will be some cases where you would have to exhaust many possible combinations to find the correct combination.  Be patient, this will get easier with practice.

Quicktime_Video_Icon  Factoring Quadratic Equations (07:28) 

Stop!  Go to Questions #20-25 about this section, then return to continue on to the next section.
The Zero Product Property

The Zero Product Property along with factoring is one method used to solve quadratic equations.


To use the zero product property
     1.)  set the quadratic equal to zero
     2.)  factor the quadratic
     3.)   set each factor = to zero and solve

Example #1:  x2 + 4x − 32 = 0
                      (x + 8)(x − 4) = 0

                      x + 8 = 0     or     x − 4 = 0
                      x = −8         or     x = 4  

The zeros or solutions to this quadratic are –8 and 4.

Example #2:  x2 = 11 x + 60                    -set the quadratic equal to zero
                      x2 = 11 x + 60 = 0
                      (x − 15)(x + 4) = 0

                      x − 15 = 0     or     x + 4 = 0
                      x = 15           or     x = −4  

The zeros or solutions to this quadratic are 15 and –4.

Quicktime_Video_Icon  Finding Roots from Factors (07:09) 

Quicktime_Video_Icon  Single Root Quadratics (03:51) 

Stop!  Go to Questions #26-30 about this section, then return to continue on to the next section.


Applications of Quadratic Functions

There are many useful real-world applications that can be found where the quadratic equation proves to be very useful.  The next few examples are just of few of the many applications of quadratic equations.

Example #1:  The height of an object launched vertically into the air from the ground at an initial velocity of 80 ft/sec can be calculated using h = 80t + 16t2 , where h is the height in feet and t is the time in seconds.

a)  How long after the object is launched will it hit the ground?
b)  How long does it take the object to reach its maximum height?
c)  How high does the object go?

Solution:

a)  How long after the object is launched will it hit the ground?

When the object returns to the ground, the height of the object is 0 feet; thus, let
h = 0 and solve for t.
h = 80t − 16t2
0 = 80t − 16t2

Solve by factoring:

0 = 16t(5 − t) -Factor out the greatest common factor.
   

16t = 0     5 − t = 0
    t = 0           t = 5

 -Apply the Zero Product Property.    

The object is on the ground at 0 seconds (before it is launched) and at 5 seconds after it is launched.

The graph of h = 80t − 16t2 shows the path of the height of the object over 5 seconds and that at 5 seconds, the height is 0. 


                                                                         t = 5, h = 0

Quicktime_Video_Icon  Quadratic Expressions and Equations

b)  How long does it take the object to reach its maximum height?

To find the time it takes the object to reach its maximum height, find the t‑coordinate of the vertex.  Since we are dealing with time and height, the vertex is in the form (time, height) or (t, h).

Put the quadratic equation in standard form.

h = 80t − 16t2
h = −16t2 + 80t

Thus, a = –16 and b = 80.

It takes the object 2.5 seconds to reach its maximum height.

c)  How high does the object go?

To find the maximum height, substitute the time (2.5 seconds) from part b into the given function.

t = 2.5

h = 80t − 16t2
h = 80(2.5) − (2.5)2
h = 200 − 100
h = 100

The height at 2.5 seconds is 100 feet.  Therefore 100 feet is the maximum height.

The vertex of the graph of h = 80t − 16t2 shows the time (2.5 seconds) at which the object reaches its maximum height (100 feet).

Quicktime_Video_Icon  Finding the Maximum Value of a Quadratic Function (02:12) 

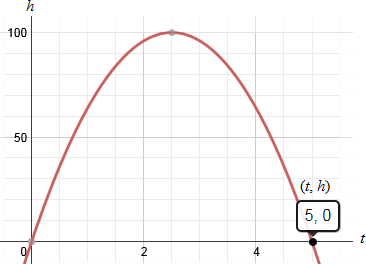
Example #2:  An arrow is shot upward with an initial speed of 112 feet per second.  When will it reach a height of 160 feet?  Use the equation h = 112t − 16t2.

Solution:  Since, we are given the equation and the height, we can find the time (t) by substituting 160 in for h in the equation and solving for t.
160 = 112t − 16t2 Substitute 160 in the formula for height.
   
16t2 − 112t + 160 = 0

Solve the equation  for zero.
 

 
16(t2 −7t + 10) = 0 Factor out the Greatest Common Factor.
   
16(t − 5)(t − 2) = 0

Factor the quadratic inside the parentheses.
   
t − 5 = 0 or t − 2 = 0

Apply the Zero Product Property.
 

 
t = 5 or t = 2 Solve for t.

Therefore, the arrow is 160 feet high both at 2 seconds (as it climbs) and at 5 seconds (as it falls) after being shot.   

Example #3:  A farmer wants to enclose a rectangular region bordering on a river using 600 feet of fence.  What is the maximum area the farmer can enclose? (No fence will be needed on the side along the river.)

Solution:  Remember the formula for the perimeter of a rectangle is P = 2l + 2w. 
Since one side of the rectangle is the river, you can take out one of the lengths and use:

P = 2w + l

Substitute 600 in for the perimeter, since the farmer has 600 feet of fencing.

600 = 2w + l

Now, think of the width as w and solve the perimeter formula for length (l).

600 = 2w + l  
600 − 2w = l -Subtract 2w from both sides.
l = 600 − 2w -Apply the property of symmetry (If A = B, then B = A).

The formula for the area of a rectangle is Area = length × width.

width = w

length = 600 − 2w

Now we can find the formula for area to represent this situation.

A = lw  
A = (600 − 2w)w -Substitute 600 −2w for l.
A = 600w − 2w2 -Distribute w over both terms within parenthesis.

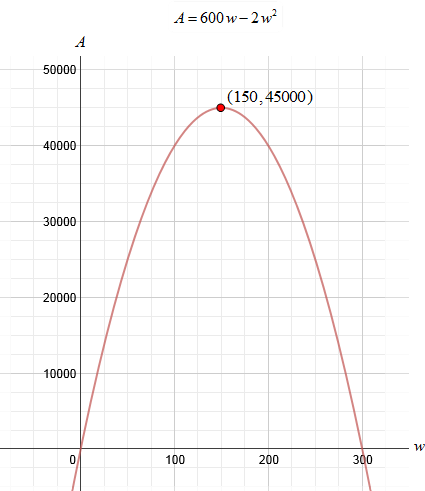
We now have a quadratic equation A = 600w − 2w2 which has a parabolic graph.  With quadratic equations, we can find a maximum vertex.  This will help us find the maximum area when dealing with a rectangular area (three sides) that is contained with 600 feet of fencing. 

The vertex will be in the form (width, area); thus, we will find the width first (x‑coordinate of the vertex), and then use that number to find the maximum area possible (y-coordinate of the vertex).

To find the vertex. 
Use the formula .

Therefore, the width of the rectangle of greatest area is 150 feet. 

To find the area, substitute w = 150 into the area formula. 

A = 600w − 2w2

A = 600(150) − 2(150)2

A = 45000

The maximum area is 45,000 square feet.

By graphing the quadratic equation, we can see that the  rectangular area with a width of 150 feet (fenced in on three sides with 600 feet of fencing) will produce a maximum area of 45,000 square feet and is the vertex point of the parabola for the quadratic equation.


question1What is the length of the rectangular area fenced in on three sides with 600 feet of
fencing that gives the maximum area?

l = 600 - 2w ... 600 - 2(150) = 300 feet

"Click here" to check the answer.


Stop!  Go to Questions #31-34 to complete this unit.



Below are additional educational resources and activities for this unit.
 
Click on the icon to find and practice topics for this unit.
 
Factoring Quadratics
 
Properties of Parabolas