MATRICES
Unit Overview
A matrix is a system of rows and columns that is used to organize numbers or data. In this unit you will learn how to add and subtract matrices, multiply a matrix by a constant and finally multiply two matrices.
Using Matrices to Represent Data
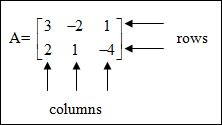
matrix: a system of rows and columns that is used as a tool for organizing numbers or data so that each position in the matrix has a purpose. element: each value in a matrix, the numbers below
|
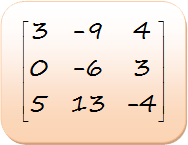
![]() In Matrix A, what number is located at a21?
In Matrix A, what number is located at a21?
The number in row two column one is 2.
"Click here" to check the answer.
Special Matrices
| row matrix: only one row column matrix: only one column square matrix: same number of rows and columns |
Two matrices are considered equal if they have the same dimensions and each element of one matrix is equal to the corresponding element of the other.
| Example #2: Solve for x and y. *Since the matrices have the same dimensions and they are equal, the corresponding elements are equal. When you write the sentences that show this equality, two linear equations are formed. To solve for x and y use either substitution or elimination.
Substitute 7 for x in either of the original equations to solve for y. The solution to the system of equations is (7, –8). |
Stop! Go to Questions #1-7 about this section, then return to continue on to the next section.
Adding or Subtracting Matrices
Matrices must have the same dimensions in order to add or subtract them. Combine the elements that have the corresponding location in the matrices.
Let's take a look a few examples.
Example #1: Add the matrices:
Example #2: Add the matrices:
|
![]() To add or subtract matrices, what must be true about their size?
To add or subtract matrices, what must be true about their size?
To add matrices the number of rows and columns must be the same.
"Click here" to check the answer.
Just like operations on real numbers, matrix addition follows some of the same properties.
 |
The zero matrix, or additive identity matrix is a matrix with all elements zero. Adding a zero matrix to a matrix leaves the matrix unchanged.
| Example #3: Add: This is an example of the Additive Identity Property in matrix addition. |
![]() What is true about the elements of the additive identity matrix?
What is true about the elements of the additive identity matrix?
Each element is a zero.
"Click here" to check the answer.
The opposite, or additive inverse of a m × n matrix A is –A, where each element is the opposite of the corresponding element of A. When the two matrices are added, the result is the zero matrix.
| Example #4: Add: This is an example of the Additive Inverse Property in matrix addition. |
![]() What is true about the elements in the second matrix when comparing the
What is true about the elements in the second matrix when comparing the
elements in the same position of the first matrix?
Each element is the additive inverse of its counterpart in the first matrix.
"Click here" to check the answer.
Let's take a look at how to apply matrices to everyday problems.
Example #5: The employees at Kennedy’s Bakery record the number of each type of cookie sold in the two stores for Monday, Tuesday and Wednesday. The sales are shown in the following table. a) Write a matrix for each store’s sales. b) Find the sum of each type of cookie sold each day expressed as a matrix. c) Find the difference in cookie sales from Store 1 to Store 2 expressed as a matrix.
a) Write a matrix for each store’s sales.
b) Find the sum of each type of cookie sold each day expressed as a matrix. Add the corresponding elements in each matrix.
c) Find the difference in cookie sales from Store 1 to Store 2 expressed as a matrix.
|
Matrices provide a useful way to organize and calculate data.
![]() Tables without Labels -- Football (02:30)
Tables without Labels -- Football (02:30)
Stop! Go to Questions #8-13 about this section, then return to continue on to the next section.
Scalar Multiplication
Multiplying a matrix by a constant, each element of the matrix is multiplied.
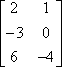
Example #1: Multiply matrix A by 3. (This is represented as 3A.) |
If scalar multiplication and addition or subtraction occurs in a problem, do the scalar multiplication first.
Example #2: Use scalar multiplication to simplify:
*Notice that the last matrix was multiplied by a (–5); therefore, it changes to addition (+ –5), and then all of the multiplications by –5 are within the matrix. |
As in operations on real numbers, matrix scalar multiplication follows some of the same properties.
 |
In the next example, we will explore the Associative Property of Scalar Multiplication.
Example #3: Show that 2(3)(A) = 2(3A) using scalar multiplication.
Solution:
Thus, 2(3)(A) = 2(3A), illustrating the associative property of scalar multiplication with matrices. |
Stop! Go to Questions #14-16 about this section, then return to continue on to the next section.
Matrix Multiplication
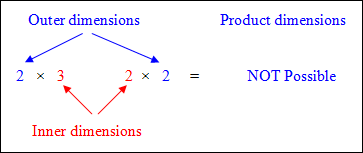
Matrix multiplication involves multiplication and addition.To multiply any two matrices, the number of columns in the first matrix must be the same as the number of rows in the second matrix.
Example #1: Multiply the matrices: 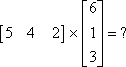
*Notice that a 1 × 3 matrix multiplied by a 3 × 1 matrix results in a 1 × 1 matrix. |
 |
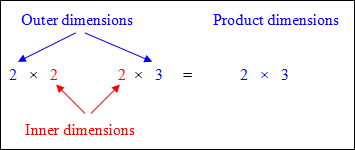
To multiply any two matrices,
(a) the inner dimensions must be the same,
(b) then the outer dimensions become the dimensions of the resulting product matrix.
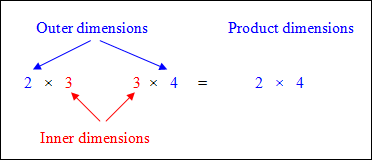 |
| Example #2: Multiply the matrices: The first matrix is a 2 × 2 matrix and the second matrix is a 2 × 3 matrix.
*Notice that you are taking the first row [5 3] and multiplying each column, then picking up the second row and multiplying each column. |
Example #3: Multiply the matrices:
*Notice that if we attempted to multiply, there would be no number in the first column of the second matrix to multiply the 3 that is located in the first row of the first matrix.
Since the inner dimensions are not the same, these two matrices cannot be multiplied. The number of columns in the first matrix must be the same as the number of rows in the second matrix. |
Now let's take another look at how to apply matrices to everyday problems.
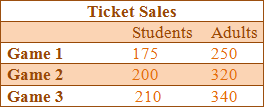
Example #4: The attendance for three basketball games is shown in the table below. Student tickets cost $3.00 each and adult tickets cost $5.00 each. (a) Write matrices to represent the attendance and the ticket cost.
(a) Set up the matrices so that the number of columns in the attendance matrix is equal to the number of rows in the cost matrix.
(b) Use matrix multiplication to show the revenue for ticket sales at each of the three games.
(c) Find the total revenue for the three games.
|
Multiplication of square (n × n) matrices has some of the properties of real number multiplication.
 |
In the next example, we will explore the Distributive Property of Matrix Multiplication.
| Example #2: Show that A(B + C) = AB + AC.
= = = = = = |
Stop! Go to Questions #17-30 to complete this unit.
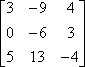 *(2
*(2 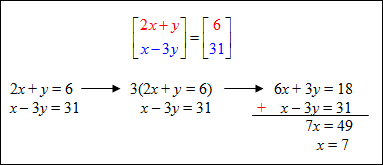
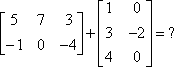

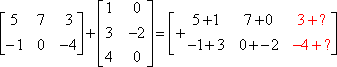

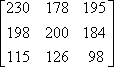
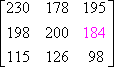 +
+ 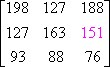 +
+ 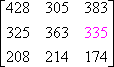
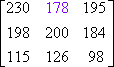 +
+  +
+ 
 3A =
3A = 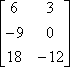
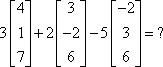
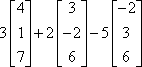 =
= 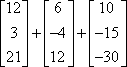 =
= 
 =
= 
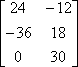
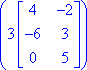 = 2
= 2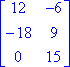
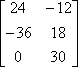
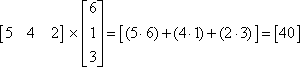

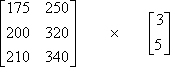
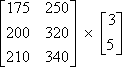 =
= 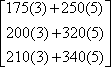 =
= 