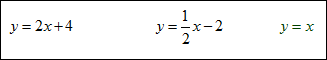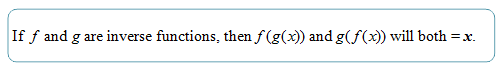FUNCTIONS AND INVERSES OF FUNCTIONS
Unit Overview
The unit begins with basic function concepts: functions as relations, domain, range, and evaluating functions. The unit continues with performing operations with functions, finding the composition and inverse of functions, and determining whether the inverse of a function is a function.
Introduction to Functions
relation: a relationship between two variables such that each value of the first variable is paired with one or more values of the second variable; a set of ordered pairs. Example #1: {(2, 4), (–4, 5), (2, –7), (0, 9)} function: a relationship between two variables such that each value of the first is paired with exactly one value of the second variable; all domain values (x-values) are different. Example #2: {(2, 4), (0, 6), (7, 4), (–9, 4)} domain: the set of all possible values of the first variable (all x-values) From example #2 above: domain = {2, 0, 7, –9} range: the set of all possible values of the second variable (all y-values) From example #2 above: range = {4, 6} |
![]() Introduction: Functions Relate Elements of Sets (02:04)
Introduction: Functions Relate Elements of Sets (02:04)
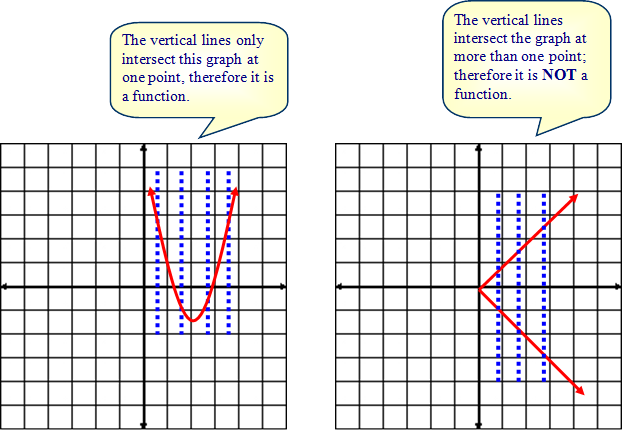
| vertical line test: If every vertical line intersects a given graph at no more than one point, then the graph represents a function. |
 |
![]() Functions, Domain, and Range -- Burning Calories (02:34)
Functions, Domain, and Range -- Burning Calories (02:34)
function notation: If there is a correspondence between values of the domain, x, and values of the range, y, that is a function; then y = f (x), and (x, y) can be written as (x, f (x)). f (x) is read “f of x”. The number represented by f (x) is the value of the function f at x. |
To evaluate a function for a specific variable, replace x with the given value and solve.
 |
Stop! Go to Questions #1-8 about this section, then return to continue on to the next section.
Operations with Functions
*functions can be combined by adding, subtracting, multiplying, and dividing.
 |
*To find restrictions on the domain, set the denominator equal to zero and solve. The result will be the restriction on the domain.
Composition of functions: when you apply a function rule on the result of another function rule, you compose the functions. |
![]() Composite Functions -- Barbeque (03:09)
Composite Functions -- Barbeque (03:09)
Let f and g be functions of x.
The composition of f with g is denoted by f o g or f ( g (x)).
To find the value of a composite function:
-place the entire second function f o (g (x)) or f ( g (x)) into the first function in place of x.
 |
Stop! Go to Questions #9-14 about this section, then return to continue on to the next section.
Inverses of Functions
The inverse of a relation consisting of the ordered pairs (x, y) is the set of all ordered pairs (y, x). (switch the x and y)
Consider the relation {(1, 2), (4, –2), (3, 2)}.- The domain of the relation is {1, 4, 3} and the range of the relation is {–2, 2}.
- The relation is a function because each domain value is paired with exactly one range value.
To find the inverse of the relation, switch the x any y values.
- The inverse is {(2, 1), (–2, 4), (2, 3)}.
- The domain of the inverse is {2, –2}.
- The range of the inverse is {1, 4, 3}.
*The relation is a function but the inverse is NOT a function because the domain value 2 is paired with two range values. {(2, 1), (–2, 4), (2, 3)}.
The range of a relation is the domain of the inverse. The domain of a relation is the range of the inverse. The inverse of a function may or may not be a function.
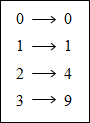
Let's consider the points in the table.
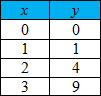 |
Is the relation a function?
Answer: The relation IS a function since each domain value (x) is paired with exactly one range value (y).
|
We denote the relation in function notation as f (x) since it is a function.
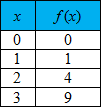 |
Is the inverse of f (x) a function?
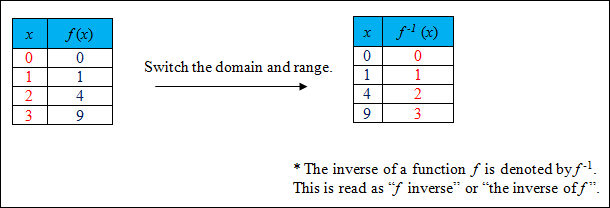 |
Answer: The inverse of the function IS a function also because each domain value is paired with exactly one range value.
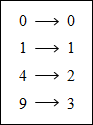 |
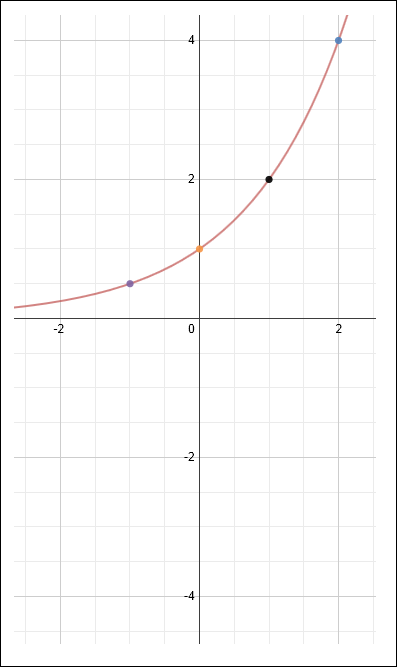
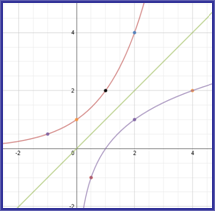
Let's examine the graph of the function and its inverse, and how they relate to the graph of y = x.
Study the given graph of the points of the function, the inverse function, and y = x.
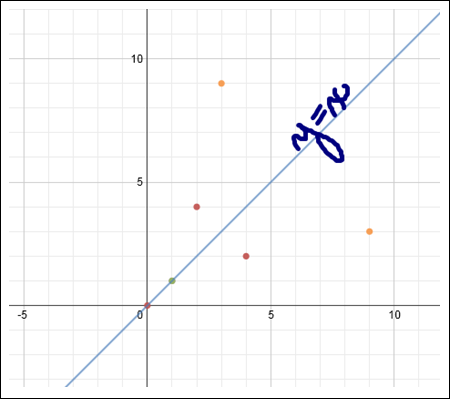 |
Do you see a relationship in the location of the points above y = x (that is f (x)) and the location of the points below y = x, (that is the inverse of f -1(x))?
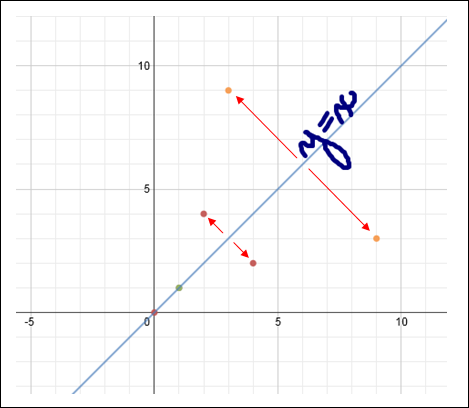 Notice that the points are a reflection of each over the graph of the line, y = x. |
The graph of a function and its inverse are reflections of each other over the line y = x.
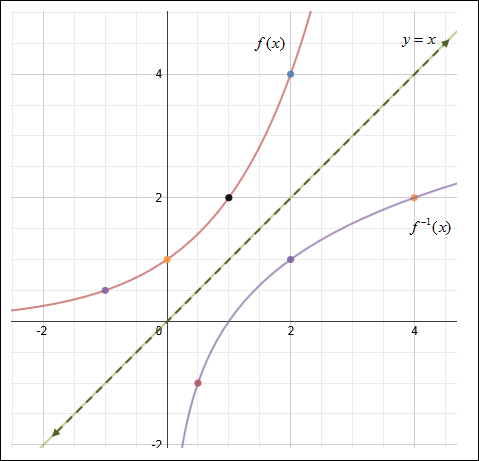
Study the graph of the two functions shown below.
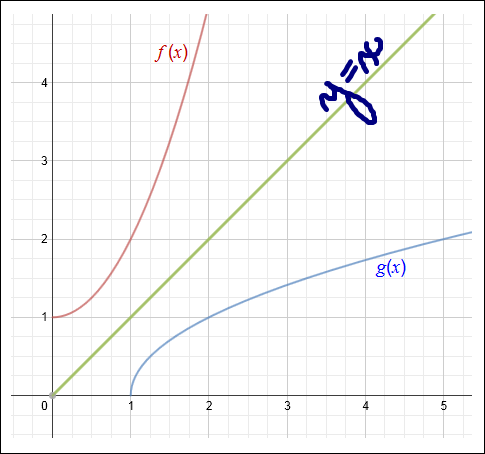 |
Notice that all the points of g (x) beginning at (0, 0) are a reflection of the points in f (x) across y = x; thus, g (x) is the inverse of f (x).
Since they are inverses, all of the domain values (x-values) in f (x) are the range values (y-values) in g (x) and all of the range values (y-values) in f (x) are the domain values (x-values in g (x)).
For example, notice that point (1, 2) in f (x) becomes point (2, 1) on g (x) when reflected across y = x.
![]() What point on g (x) is the inverse of point (0, 1) on f (x)?
What point on g (x) is the inverse of point (0, 1) on f (x)?
The reflected point is (1, 0).
"Click here" to check the answer.
![]() In general, any point (x, y) in f (x) becomes what ordered pair in its inverse, g (x)?
In general, any point (x, y) in f (x) becomes what ordered pair in its inverse, g (x)?
( y, x )
"Click here" to check the answer.
If a function is defined by an equation, then the inverse of the function is found by switching the x and y in the equation, and then solving the new equation for y.
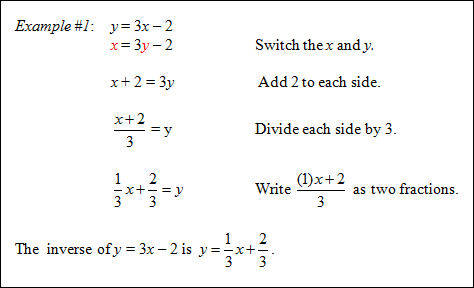 |
Now, let's graph the equations. Notice that the graphs are inverses of each other and reflected across the line, y = x.
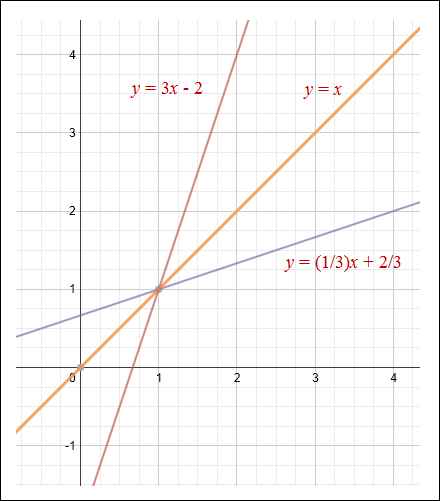 |
Sometimes the equation is written in function notation as in the following two examples. To keep the computations simple, we remember that f (x) can be written as y and vice versa.
 |
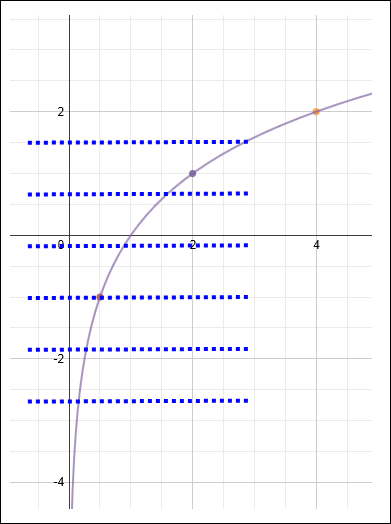
The horizontal line test is a quick test used to determine if the inverse of a function is a function graphically.
The inverse of a function is a function, if and only if, every horizontal line intersects the graph of the given function at no more than one point.
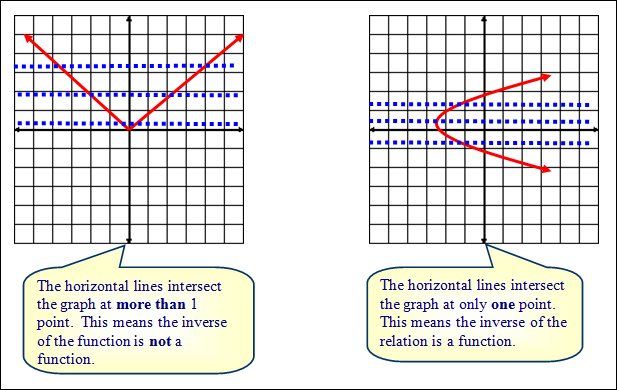 |
Example #4: Given the graph of function f as shown, sketch the graph of f -1. Is the inverse relation a function?
Solution: Because the graph of f passes through the points (–1, 0.5), (0, 1), (1, 2), and (2, 4), the graph of f -1 must pass through the points (0.5, –1), (1, 0), (2, 1) and (4, 2 ). *Plot the points and draw a smooth curve through the points. *We switch the x and y values for the inverse. The graph looks like this.
Notice that the graph of f is symmetric to the graph of f -1 with respect to the graph of the line y = x. If the graph were folded along the dashed line, the graph of f would lie on top of the graph of f -1. This is a characteristic of all graphs of functions and their inverses. Test the reflection characteristic of functions and their inverses. Click here to view and print out the graph. Fold the paper along the dotted line, y = x. |
![]() Does the graph of f lie on top of the graph of f -1 ?
Does the graph of f lie on top of the graph of f -1 ?
Yes!
"Click here" to check the answer.
To determine whether f -1 is a function, use the horizontal line test.
Any horizontal line drawn through the graph of f -1 will intersect the graph at only one point. Thus, f -1 IS a function. |
Example #5: Graph the following functions on one set of coordinate axes.
To practice graphing functions and their inverses go to www.desmos.com/calculator or use a graphing calculator. |
![]() Are the functions reflections of each other over y = x?
Are the functions reflections of each other over y = x?
Yes!
"Click here" to check the answer.
![]() Are y = 2x + 4 and y =
Are y = 2x + 4 and y = ![]() − 2 inverses of each other?
− 2 inverses of each other?
Yes!
"Click here" to check the answer.
Notice that the graphs of the functions are symmetric to the line y = x and inverses of each other.
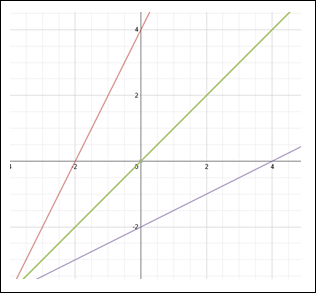 |
Another way to determine whether two functions are inverses of each other is by finding both of their compositions.
|
Stop! Go to Questions #15-33 to complete this unit.