NEGATIVE NUMBERS AND COORDINATE GRAPHING
In the real world, often times there is a need to represent numbers below zero which we call negative numbers. We will look at the meaning of negative numbers.
Graphing in the coordinate plane has lots of practical uses. We use a coordinate graphing system to map points on a map. We’ll look at an all positive coordinate system, and then we will extend our knowledge of coordinate graphing to include the negative numbers.
Exploring Negative Numbers In the real world often times there is a need to represent numbers below zero which we call negative numbers. A number line that includes negative numbers would look like this.
Here is an example of the use of negative numbers.
|
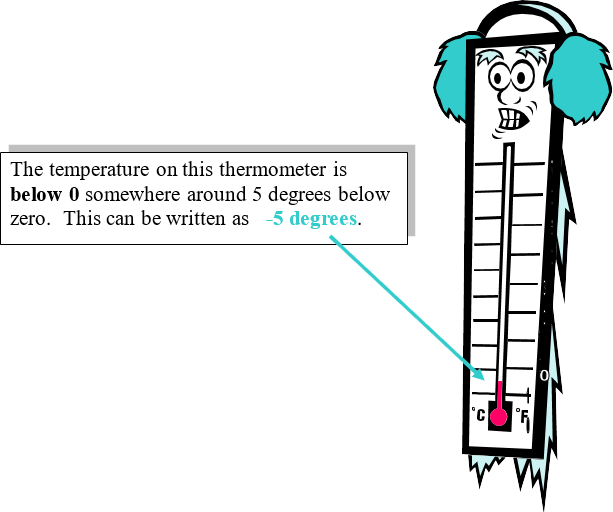
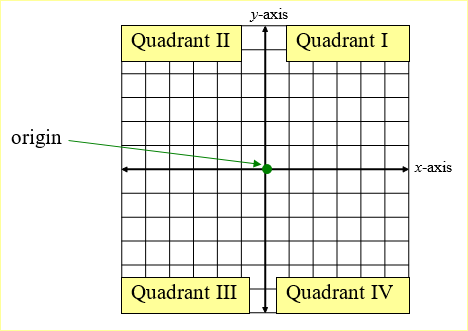
Graphing in Quadrant I of the Coordinate Plane In a coordinate plane, points may be located by plotting them. The coordinate plane is divided into four quadrants by the x–axis and the y-axis. The starting point, the origin, is the center, or point where the x and y axis intersect (cross).
A point is designated by both an x-coordinate and a y-coordinate. The origin's coordinates would be (0, 0). The x-coordinate is the first number and the y-coordinate is the second number.
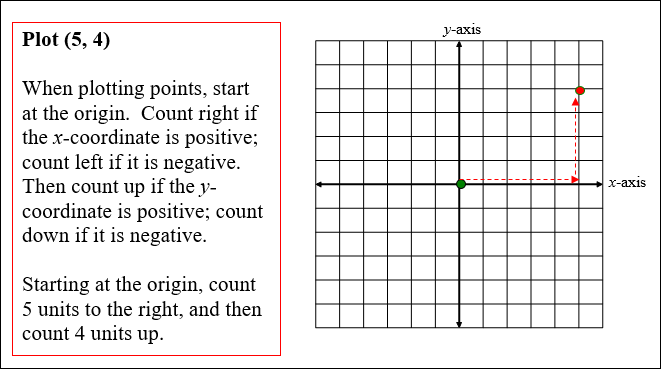
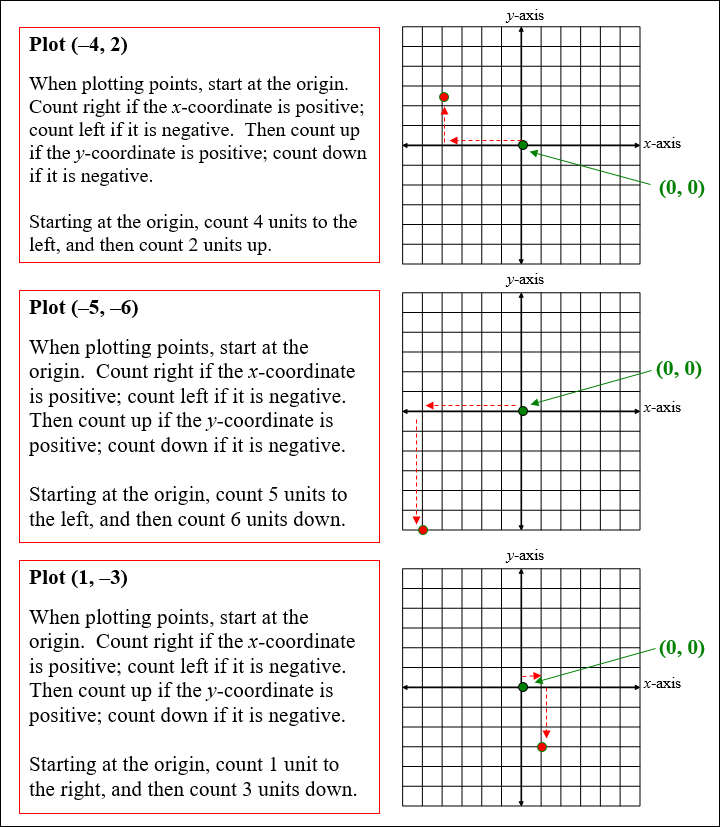
The x-coordinate is how far you count right or left of the origin. The y-coordinate is how far you then count up or down. A point's location is written as an ordered pair (x, y).
|
Graphing in Quadrants II, III, and IV In these graphs, each space represents one unit. The starting point is the origin whose coordinates are (0, 0). |
 |
 Click on the icon to find and practice topics for this unit. |
| Unit 29 Graphing Worksheet |
| Click here to watch the video on the coordinate plane. |
| Unit 29 Identify It Activity |
