Squares, Trapezoid, and
Rhombus
Unit
Overview
In this unit, learners will delve into the
geometrical nuances of squares, trapezoids, and kites, three distinct types of
quadrilaterals. The journey begins with squares, where we explore their
defining features such as four equal sides, right angles, and the properties
shared with rectangles and rhombuses, like congruent diagonals and being
parallelograms. The focus then shifts to trapezoids, distinguished by a single
pair of parallel sides, and we'll examine their variations including isosceles,
scalene, and right trapezoids, alongside formulas for calculating their area
and perimeter. Finally, the spotlight turns to kites, unique for their two
pairs of adjacent equal sides and intersecting diagonals at right angles.
Square
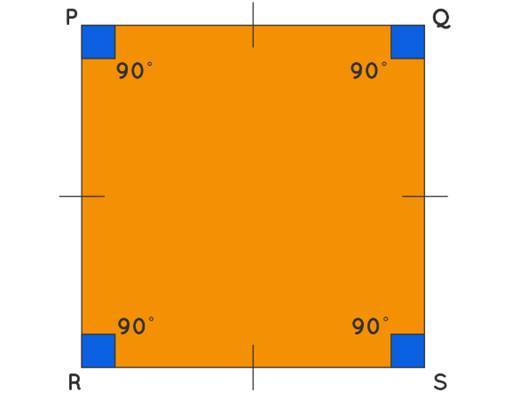
A square is a fundamental geometric shape, characterized by its quadrilateral form with four equal sides. It's a prevalent shape in our surroundings, notable for its equal sides and right angles (90°). This guide delves into the square's attributes, formulas, and construction.

What is a Square?
A square is a two-dimensional shape (2D) with four sides of equal length. The sides are not only equal but also parallel, forming a simple yet distinct figure.
A square is a type of quadrilateral, defined
by:
In this video, you will learn that the square
has the following properties: All the properties of a rhombus apply - the ones
that matter here are parallel sides, diagonals are perpendicular bisectors of
each other, and diagonals bisect the angles. All the properties of a rectangle
apply - the only one that matters here is diagonals are congruent.
Properties of a Square
A square's properties are numerous, including:
Common Properties of a Square and Rectangle
Squares and rectangles share several
properties:
Formulas of a Square
Squares have three essential formulas:
1.
Area: The area represents
the space it occupies, calculated as Area = s² (where 's' is the side length).
It's measured in square units (cm², m², etc.).
2.
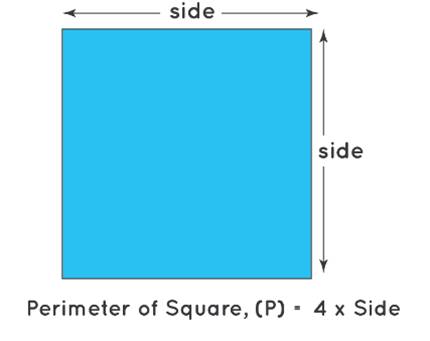
Perimeter: The perimeter is the
total boundary length, calculated as Perimeter = 4 × Side. It's expressed in
linear units (cm, m, inches, etc.)
3.
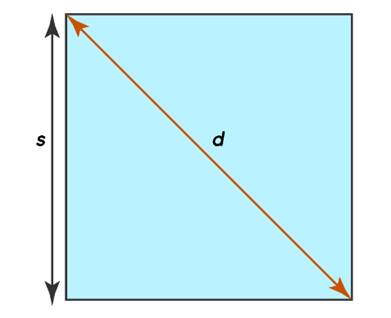
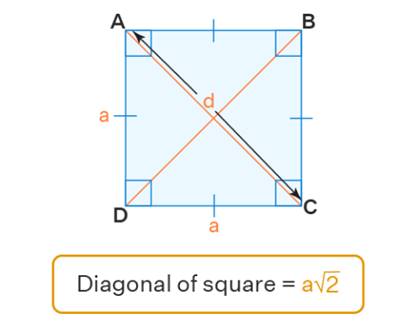
Diagonal: The diagonal is a
line segment joining two non-adjacent vertices. Using Pythagoras theorem, the
diagonal formula is Diagonal (d) = √2 × a (where 'a' is the side length).
These formulas and properties make the square a
vital component in geometry, with practical applications in various fields.
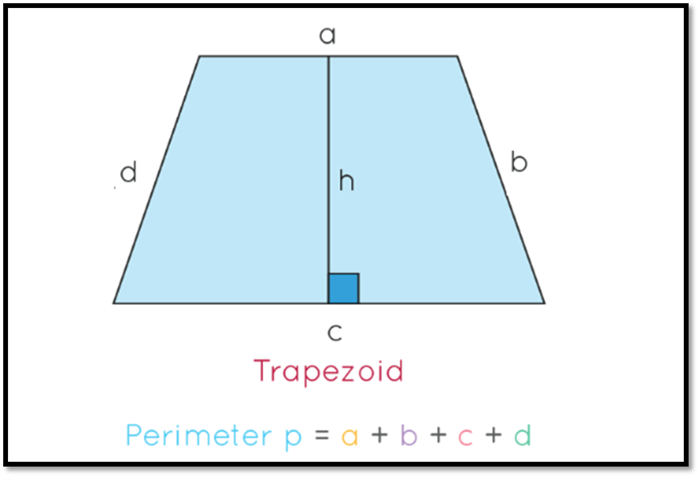
Trapezoid
The trapezoid, also known as a trapezium in
some regions, is a unique quadrilateral recognized for its varied
interpretations based on geographical location. This four-sided polygon is
distinguished by having one pair of opposite sides parallel, known as the
bases, while the other sides, referred to as the legs, are non-parallel.

A trapezoid is a closed 2D figure with two
parallel sides termed as bases. The non-parallel sides are the legs. The
altitude, or the shortest distance between the bases, is a crucial dimension
for calculating its area.
In this video, you will learn to use and
apply the properties of trapezoids
Properties
of a Trapezoid
Trapezoids are known for their unique features:
·
Parallel bases.
·
In an isosceles
trapezoid, opposite sides are equal.
·
Adjacent angles sum up
to 180°.
·
The median
(mid-segment) is parallel to the bases and its length is the average of the
bases.
·
A trapezoid becomes a
parallelogram if both pairs of opposite sides are parallel.
·
Under certain
conditions (all sides parallel and equal, right angles), a trapezoid can be
considered a square or a rectangle.
Types of
Trapezoids
Trapezoids are categorized into three main
types:
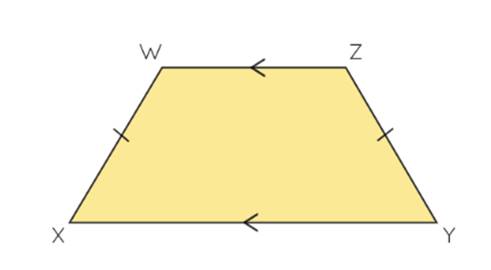
1.
Isosceles Trapezoid: This type has equal
non-parallel sides, equal base angles, a line of symmetry, and equal diagonals.
2.
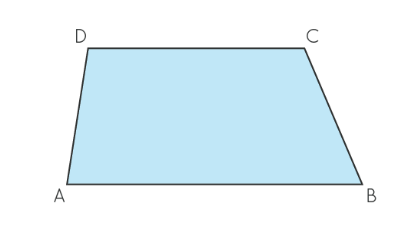
Scalene Trapezoid: Here, neither sides
nor angles are equal.
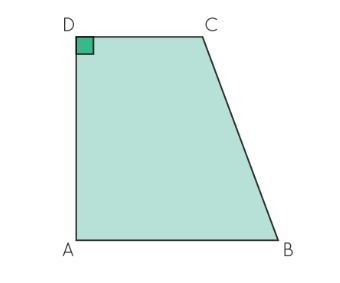
3.
Right Trapezoid: Characterized by a
pair of right angles.
Trapezoid
Formulas
The primary formulas for a trapezoid are for
its area and perimeter:
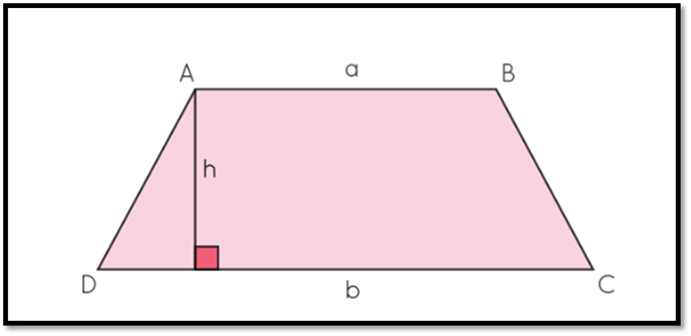
·
Area: Calculated as the
product of the average of the bases and the altitude A = [(a + b)/2] × h.
·
Perimeter: The sum of all sides Perimeter = a + b + c + d).
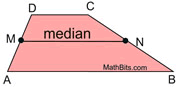
Theorem of
a Trapezoid
(1) The median of a trapezoid is parallel to the
bases and half the sum of the lengths of the bases.
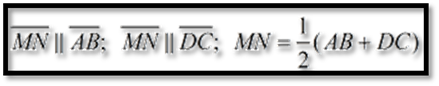
Theorem of
an Isosceles Trapezoid
(2) If a quadrilateral (with one set of parallel sides) is an isosceles
trapezoid, its legs are congruent.
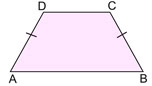
(3) If a quadrilateral is an isosceles trapezoid, the diagonals are
congruent.
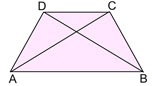
(4) (converse) If a trapezoid has congruent diagonals, it is
an isosceles trapezoid.
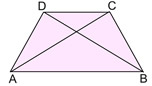
(5) If a quadrilateral is an isosceles trapezoid, the opposite angles
are supplementary.
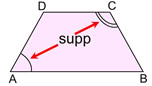
(6) (converse) If a trapezoid has its opposite angles
supplementary, it is an isosceles trapezoid.

Kite
A kite, in the realm of geometry, is a distinct
type of quadrilateral characterized by two pairs of adjacent sides of equal
length. This shape stands out due to its intersecting diagonals that form a
right angle. Let's delve deeper into the kite's properties.
A kite is a quadrilateral where two pairs of adjacent sides are of equal length. Unlike some other quadrilaterals, a kite does not have parallel sides, but it does feature one pair of equal opposite angles.
Properties
of a Kite
The kite, with its unique structure, exhibits
the following properties:
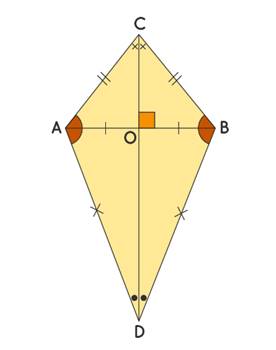
·
Two pairs of adjacent
sides are equal in length.
·
One pair of opposite
angles, typically the obtuse angles, are equal.
·
The longer diagonal
bisects the shorter diagonal and the kite itself into congruent triangles.
·
The diagonals intersect
at right angles (90°).
·
The shorter diagonal
divides the kite into two isosceles triangles.
·
The longer diagonal
creates two congruent triangles by the Side-Side-Side (SSS) criterion of
congruence.
·
The area of a kite is
half the product of its diagonals.
·
The perimeter is the
sum of all its sides.
·
The sum of its interior
angles equals 360°.
Angles in a Kite
Regarding the angles of a kite:
·
The four interior
angles total 360°, as with any quadrilateral.
·
One pair of
non-adjacent angles (the obtuse angles) are equal.
Diagonals of a Kite
The diagonals of a kite have these notable
features:
·
They differ in length,
with the longer diagonal bisecting the shorter.
·
They intersect at right
angles.
·
The shorter diagonal
forms two isosceles triangles.
·
The longer diagonal
forms two congruent triangles based on the SSS congruence.
Theorems of
a Kite
Definition and Theorems pertaining to a kite:
|
|||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
Important Notes
Key takeaways about a kite include:
·
It is a type of
quadrilateral.
·
It fulfills all
properties of a cyclic quadrilateral.
·
Its area is calculated
as half the product of its diagonals.
Understanding these properties provides a
comprehensive view of the kite, highlighting its unique place in geometry.
Quadrilateral
Properties Quiz