Parallelograms,
Rectangles, and Rhombus
Unit
Overview
You will learn to differentiate between various
types of parallelograms, such as squares, rectangles, and rhombuses, by
examining their unique features. This knowledge will enable them to effectively
identify and analyze these shapes in geometric problems, enhancing their
spatial reasoning and problem-solving skills in the context of geometry.
Quadrilateral
Game
A quadrilateral has four sides, is
two-dimensional, closed, and has straight sides. There are five types of
quadrilaterals. Before you begin your exploration of quadrilaterals and their
properties, see if you can correctly identify important vocabulary terms.
Parallelograms
A parallelogram is a four-sided figure where
opposite sides are not only parallel but also of equal length. This shape
features four angles located at its corners. Comprehending the characteristics
of parallelograms aids in connecting its angles and sides more effortlessly.
Furthermore, these properties are beneficial in solving mathematical problems
that involve the lengths and angles of a parallelogram.
In this video, you will learn the important
properties of parallelograms and how to apply them.
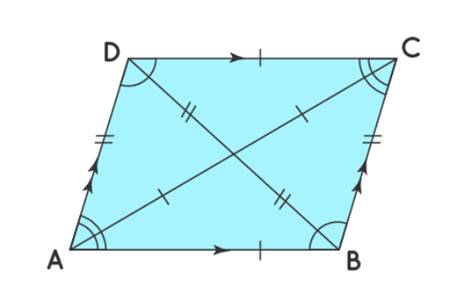
Angle Properties of a Parallelograms
The important properties of parallelograms
related to angles are as follows:
·
The opposite angles of a parallelogram are equal, i.e., ∠A = ∠C, and ∠B = ∠D.
·
All the angles of a parallelogram add up to 360°, i.e., ∠A + ∠B + ∠C + ∠D = 360°.
·
The consecutive angles of a parallelogram are supplementary,
i.e.,
o
∠A + ∠B = 180°
o
∠B + ∠C = 180°
o
∠C + ∠D = 180°
o
∠D + ∠A = 180°

Side Properties of a Parallelogram
The opposite sides of a parallelogram are equal
and parallel to each other.
Observe the following figure to understand the
properties of a parallelogram.
The properties mentioned apply to all kinds of
parallelograms, but it's also important to explore the unique characteristics
of certain special types of parallelograms. These include squares, rectangles,
and rhombuses, each distinct in its properties, yet all falling under the broad
classification of parallelograms.
Property
|
Square
|
Rectangle
|
Rhombus
|
Sides
|
All four sides are
equal.
|
The opposite sides
are equal and parallel.
|
All sides are equal
in length.
|
Angles
|
All four angles are
90°.
|
All four angles are
90°.
|
The sum of any two
adjacent interior angles is 180°.
|
Diagonals
|
Bisect the angles;
same length.
|
Same length.
|
Bisect each other at
90°.
|
Opposite Sides
|
Equal and parallel.
|
Equal and parallel.
|
Equal and parallel.
|
This table summarizes the distinct properties
of squares, rectangles, and rhombuses, highlighting their similarities and
differences within the context of parallelograms.
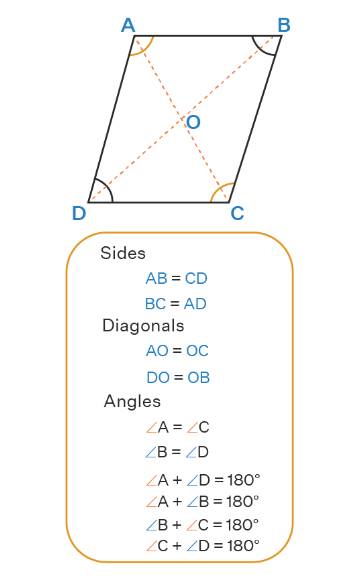
Properties of Parallelogram Diagonals
First, let's review what a diagonal is.
Diagonals are line segments connecting non-adjacent vertices in any polygon.
For instance, in parallelogram ABCD (as shown in the below figure), AC and BD
serve as the diagonals. Suppose O is the point where diagonals AC and BD
intersect.
The characteristics of a parallelogram's
diagonals include:
Theorems
on Parallelogram Properties
The theorems concerning the properties of
parallelograms are crucial for establishing guidelines to solve problems
involving these shapes. They make it simpler to comprehend and apply the
relationships between the sides and angles of a parallelogram in various
mathematical problems. Additionally, these theorems aid in grasping concepts
related to other types of quadrilaterals. Four key theorems relevant to
parallelogram properties include:
1.
The opposite sides of a
parallelogram are of equal length.
2.
The opposite angles of
a parallelogram are equal in measure.
3.
The diagonals of a
parallelogram bisect each other at their intersection point.
4.
In any quadrilateral,
if a pair of opposite sides is both equal in length and parallel, then the
shape is a parallelogram.
Theorem 1: In a Parallelogram the Opposite Sides are
Equal.
Given: ABCD is a parallelogram.
To Prove: The opposite sides are equal, AB =
CD and BC = AD.
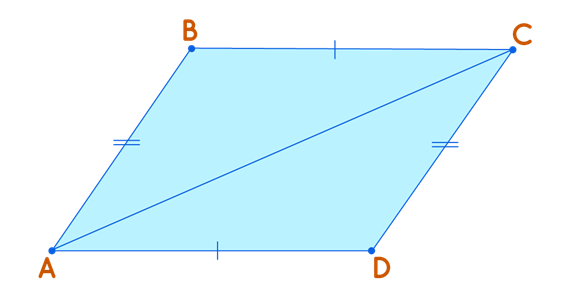
In parallelogram ABCD, compare triangles ABC
and CDA. In these triangles:
Hence by the ASA criterion, both the triangles
are congruent and the corresponding sides are equal. Therefore,
we have AB = CD, and BC = AD.
Converse of Theorem 1: If the opposite sides in a
quadrilateral are equal, then it is a parallelogram.
Given: The opposite sides in a quadrilateral
ABCD are equal, AB = CD, and BC = AD.
To Prove: ABCD is a parallelogram.
In the quadrilateral ABCD we are given that AB
= CD and AD = BC. Now compare the two triangles ABC, and CDA. Here we have
Thus by the SSS
criterion, both the triangles are congruent, and the corresponding angles are
equal. Hence we can conclude that ∠BAC = ∠DCA, and ∠BCA = ∠DAC.
Therefore AB || CD, BC || AD, and ABCD is a
parallelogram.
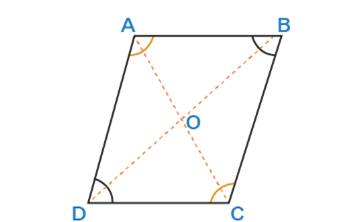
Theorem 2: In a Parallelogram, the Opposite Angles are
Equal.
Given: ABCD is a parallelogram, and ∠A, ∠B, ∠C, ∠D are the four angles.
To Prove: ∠A = ∠C and ∠B = ∠D
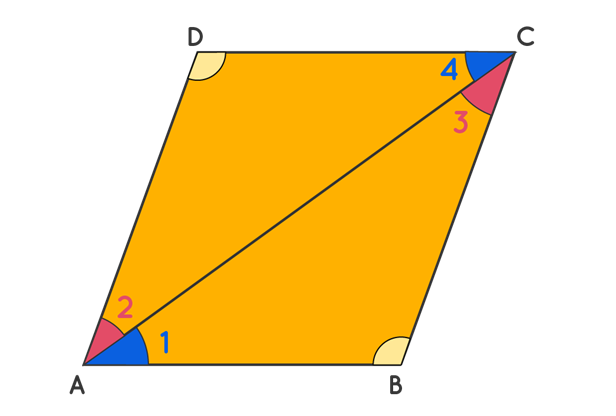
Let us assume that ABCD is a parallelogram. Now
compare triangles ABC and CDA. Here we have,
Thus, by ASA, the two triangles are
congruent, which means that ∠B = ∠D. Similarly, we can show that ∠A = ∠C. This proves that opposite angles in any parallelogram are
equal.
Converse of Theorem 2: If
the opposite angles in a quadrilateral are equal, then it is a parallelogram.
Given: ∠A = ∠C and ∠B = ∠D in the quadrilateral ABCD.
To Prove: ABCD is a parallelogram.
Assume that ∠A = ∠C and ∠B = ∠D in the parallelogram ABCD given above. We have to prove that
ABCD is a parallelogram. We have:
∠A + ∠B + ∠C + ∠D = 360º
2(∠A + ∠B) =360º
∠A + ∠B = 180º.
This must mean that AD || BC. Similarly, we can
show that AB || CD. Hence, AD || BC, and AB || CD. Therefore, ABCD is a
parallelogram.
Theorem 3: Diagonals of a Parallelogram Bisect Each Other.
Given: PQTR is a parallelogram. PT and QR are
the diagonals of the parallelogram.
To Prove: The diagonals PT and RQ bisect
each other, i.e., PE = ET and ER = EQ.
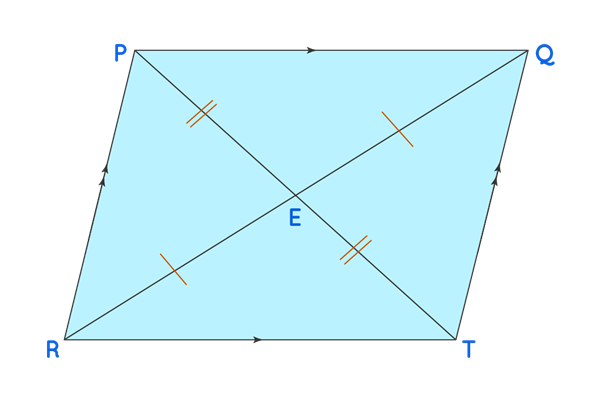
First, let us assume that PQTR is a
parallelogram. Compare triangles TER and triangle PEQ. We have,
By the ASA criterion, the two triangles are
congruent, which means by CPCTC, PE = ET, and RE = EQ. Thus, the two diagonals
PT and RQ bisect each other, and PE = ET and ER = EQ.
Converse of Theorem 3: If
the diagonals in a quadrilateral bisect each other, then it is a parallelogram.
In the quadrilateral PQTR, if PE=ET and ER=EQ, then it is a
parallelogram.
Given: The diagonals PT and QR bisect each
other.
To Prove: PQRT is a parallelogram.
Proof: Suppose that the diagonals PT and QR
bisect each other. Compare triangle RET, and triangle PEQ once again. We have:
Hence by the SAS criterion, the two
triangles are congruent. This means that ∠QRT = ∠PQR, and ∠PRT = ∠QPT. Hence, PQ || RT, and RT || QT. Thus, PQRT is a
parallelogram.
Theorem 4: If One Pair of Opposite Sides is Equal and
Parallel in a Quadrilateral then it is a Parallelogram.
Given: It is given that AB = CD and AB || CD.
To Prove: ABCD is a parallelogram.
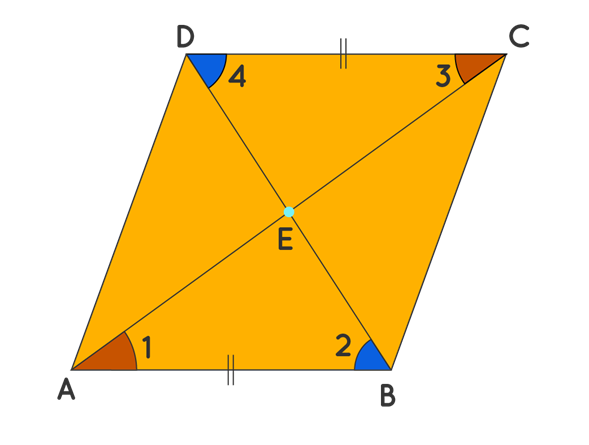
Let us compare the triangle AEB and triangle
CED. We have,
Thus, by ASA criterion, the two triangles
are congruent. Hence we can conclude that by CPCTC, AE = EC, and BE = ED.
Therefore, the diagonals AC and BD bisect each other, and this further means
that ABCD is a parallelogram.
Important Notes:
A quadrilateral is a parallelogram when:
·
The opposite sides of a
quadrilateral are equal and parallel.
·
The opposite angles of
a quadrilateral are equal.
·
The diagonals bisect
each other.
·
One pair of opposite
sides is equal and parallel.
Properties of
Parallelograms
In this interactivity, you are going to look
further at the properties of parallelograms. This will help you interpret
geometry symbols in diagrams.
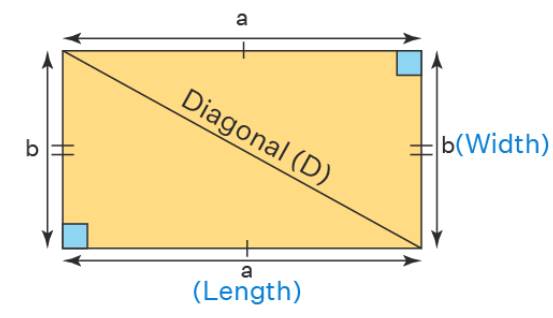
Rectangles
A rectangle, a unique type of quadrilateral, is
characterized by its equiangular nature, meaning all four of its angles are
right angles. This shape also features opposite sides that are not only
parallel to each other but are of equal length as well. Within a rectangle, the
longer sides are referred to as the length, while the shorter sides are known
as the width. These features collectively set the rectangle apart from other
quadrilateral shapes.
In this video, you will learn how to apply the
properties of a rectangle.
Properties of a Rectangle
A rectangle can be quickly recognized by its distinct properties. It is a two-dimensional shape with four sides, four vertices, and four angles. The key features of a rectangle include opposite sides that are both parallel and equal in length. As a special type of quadrilateral, all angles in a rectangle are right angles, each measuring 90°. This means that while a rectangle has four sides, they are not all of equal length; only the opposite sides match in length. In everyday life, we encounter numerous examples of rectangles, such as kites, paintings, slabs, and storage boxes, illustrating its common presence in our surroundings.
To deepen your understanding of rectangles,
consider these properties while visualizing the shape:
1.
A rectangle is a
quadrilateral, which means it has four sides. Each of its interior angles is
equal, each measuring 90°, making it an equiangular quadrilateral.
2.
The opposite sides of a
rectangle are both equal in length and parallel to each other.
3.
At every vertex of a
rectangle, the interior angle is a right angle (90°).
4.
The sum of all interior
angles in a rectangle adds up to 360°, a characteristic it shares with all
quadrilaterals.
5.
The diagonals of a
rectangle bisect each other, meaning they cut each other in half at the point
where they intersect.
6.
Both diagonals of a
rectangle are of equal length.
7.
The length of a
rectangle's diagonal can be calculated using the Pythagorean theorem.
For sides of lengths a and b, the diagonal's length is:
![]()
8.
A rectangle is a type
of parallelogram, a broader category of quadrilaterals with opposite sides that
are parallel.
9. While all rectangles are parallelograms due to their parallel sides, not all parallelograms are rectangles. This is because a parallelogram does not necessarily have all angles equal to 90°, a defining feature of rectangles.
Formulas of a Rectangle
Understanding the geometry of a rectangle
involves mastering three fundamental formulas related to its area, perimeter,
and diagonal length:
1.
Area of a Rectangle: The area (A) of a
rectangle is calculated by multiplying its length (l) by its width (w). This
formula is expressed as A = l × w. The area represents the
amount of space enclosed within the rectangle.
2.
Perimeter of a
Rectangle:
The perimeter (P) is the total distance around the edge of the rectangle. It is
calculated by adding the lengths of all four sides, which simplifies to P =
2 (l + w), since opposite sides of a rectangle are equal in
length.
3.
Diagonal of a Rectangle: The length of the
diagonal (d) can be found using the Pythagorean theorem, as a rectangle forms a
right triangle when split along its diagonal. The formula for the diagonal is d
=
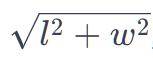 where l is the length and w is the width of the rectangle. The diagonal connects two
opposite vertices of the rectangle.
where l is the length and w is the width of the rectangle. The diagonal connects two
opposite vertices of the rectangle.
Each of these formulas captures a different
aspect of the rectangle's geometry and is essential for various calculations
involving rectangular shapes.
Theorems Related to a Rectangle
A rectangle is a parallelogram characterized by
having four right angles.
Theorem 1 – click the
image below for the Proof.
Theorem 2 (Converse)- click the image below for the Proof.
From the above definitions and theorems, we can
infer a fundamental property of rectangles in the realm of geometry. The first
theorem establishes that in a rectangle, which is a specific type of
parallelogram, the diagonals are always congruent. This characteristic is a
direct result of the right angles present in a rectangle. Conversely, the
second theorem provides a significant criterion for identifying a rectangle: if
a parallelogram has diagonals of equal length, it can be conclusively
identified as a rectangle. These theorems not only reinforce the unique
properties of rectangles but also provide a practical method for distinguishing
rectangles from other parallelograms in geometric studies.
Quadrilaterals
Family Tree
There are many different types of
quadrilaterals. Before you use direct proofs to prove the properties of
quadrilaterals, test your knowledge of these figures in this interactivity.
Rhombus
A rhombus can be primarily defined as a
quadrilateral in which all four sides are of equal length. This characteristic
inherently classifies a rhombus as a type of parallelogram, as the property of
having four congruent sides is exclusive to parallelograms within the family of
quadrilaterals. Alternatively, a rhombus can be described as a parallelogram
that has at least two adjacent sides that are congruent. This alternative
description, while accurate, represents a specific case of the more general
characteristic of a rhombus, where all sides are equal. Both definitions
emphasize the unique geometrical properties that distinguish a rhombus from
other quadrilaterals.
In this video, you learn how to apply the
properties of a rhombus.
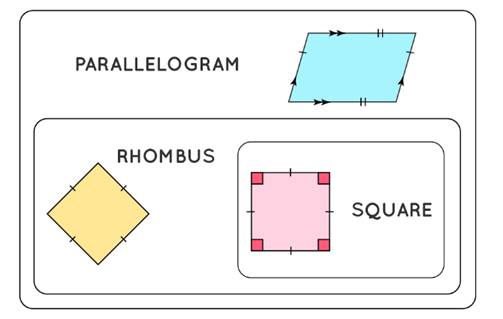
From the given figure, it's evident that every
rhombus is a parallelogram due to its four congruent sides, a defining feature
of parallelograms. However, the converse is not true: not all parallelograms
are rhombuses, as a parallelogram only requires opposite sides to be equal, not
necessarily all four sides. A square is a special type of rhombus characterized
by four equal sides and right angles at each corner. While the angles in a general
rhombus do not need to be right angles, if a rhombus has right angles, it is
classified as a square. Therefore, we can summarize these observations as
follows:
·
Every rhombus (or
rhombi) is a parallelogram, but not every parallelogram is a rhombus.
·
Not all rhombi are
squares, but every square is a rhombus by definition.
Additionally, a rhombus is known by other
names, such as a diamond, lozenge, or simply as a rhomb, reflecting its
versatile nature in geometry.

Properties
of a Rhombus
A rhombus is
acknowledged as a special type of parallelogram, inheriting all the fundamental
properties of a parallelogram while also exhibiting its own unique
characteristics. The defining feature of a rhombus is that all of its sides are
congruent, which sets it apart from other parallelograms.
One of the key
features of a rhombus is its symmetry. It possesses two lines of symmetry,
which are its diagonals. An axis of symmetry is a line that divides a shape
into two mirror-image halves. In the case of a rhombus, each diagonal act as
such an axis, reflecting the halves of the rhombus over these lines. This
characteristic is referred to as reflection symmetry.
The general
properties of a parallelogram, which also apply to a rhombus, include:
1.
Opposite angles are congruent or equal.
2.
Opposite sides are equal in length and parallel to each other.
3.
The diagonals bisect each other, meaning they cross at their midpoint.
4.
The sum of any two adjacent or consecutive angles is 180°, making them
supplementary.
In addition to these,
a rhombus has specific properties that distinguish it from other
parallelograms. These unique properties of a rhombus include:
·
All four sides are equal in length.
·
The diagonals bisect each other at
right angles.
·
The diagonals bisect the internal
angles of the rhombus.
These properties not
only define a rhombus but also help in differentiating it from other
quadrilaterals in geometric studies.
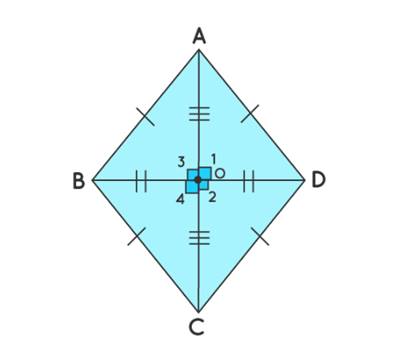
Properties of Rhombus
|
Reference
|
All sides of a
rhombus are congruent (equal).
|
Here, AB = CD = DA
= BC
|
Diagonals bisect
each other at 90° or we can also say that each of the two diagonals in a
rhombus is the perpendicular bisector of the other.
|
Here, diagonals DB
and CA bisect each other at 90°
|
Opposite angles are
equal and the opposite sides are parallel.
|
Here, CD || AB and
BC || AD.
∠A = ∠C and ∠D = ∠B
|
Adjacent angles add
up to 180°
|
∠A + ∠B = 180°
∠B + ∠C = 180°
∠C + ∠D = 180°
∠A + ∠D = 180°
|
One thing we should
remember about the diagonal of a rhombus is that in addition to bisecting each
other at 90°, the two diagonals bisected will be of the same length. For
example: if the length of a diagonal is 10 cm and the other diagonal bisects
it, then it is divided into two 5 cm segments. If you know the side of the
rhombus and the value of certain angles, then you can determine the length of
the diagonal.
Important Notes on Rhombus
Here is a list of a few points that should be
remembered while studying about rhombus:
·
Adjacent angles in a
rhombus are supplementary, they sum up to 180°.
·
Diagonals bisect each
other at right angles.
·
All squares are
rhombuses, but not all rhombuses are squares.
Parallelogram,
Rectangle, or Rhombus
Take a moment to view the defining characteristics
of parallelograms, rectangles, and rhombi in this interactivity.