Unit Circle Introduction and Conversion of Radians and Degrees

 

 

 

 

 

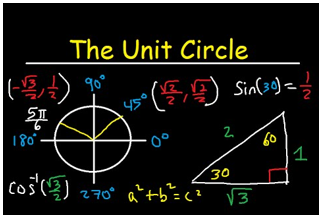
Unit Circle Introduction

 

 

 

 

 

 

Section Overview

·      To enable students to become familiar with the unit circle.

·      To use the unit circle to evaluate the trigonometric functions sin, cos, and tan for all angles.

 

Key Vocabulary:

Positive and Negative Angles - Positive angles can be found in Quadrants I & II. Negative angles can be found in Quadrants III & IV.

 

Coterminal Angles - Two angles are coterminal if they are drawn in the standard position and both have their terminal sides in the same location.


Quadrant Angle - An angle with terminal side on the x-axis or y-axis. 0° 90° 180° 270° 360°

 

 

 

What is the Unit Circle?
The unit circle has a radius of one. The intersection of x and y-axes (0, 0) is known as the origin. The angles on the unit circle can be in degrees or radians.

 

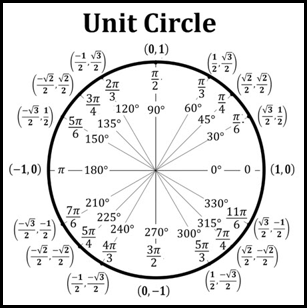
The circle is divided into 360 degrees starting on the right side of the x-axis and moving counterclockwise until a full rotation has been completed. In radians, this would be 2π.


 

 

 

 

 

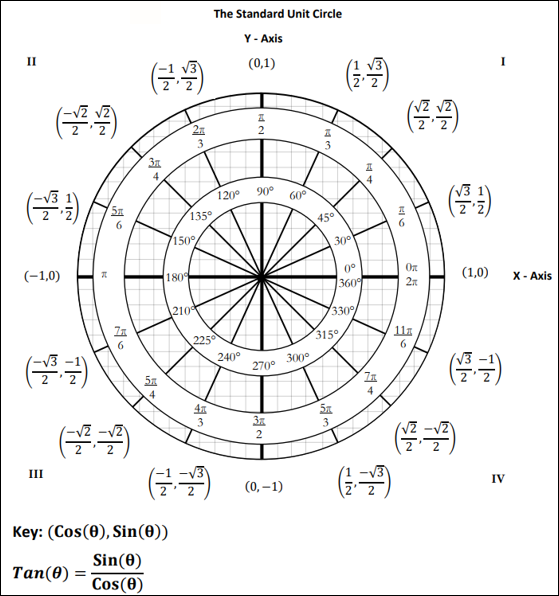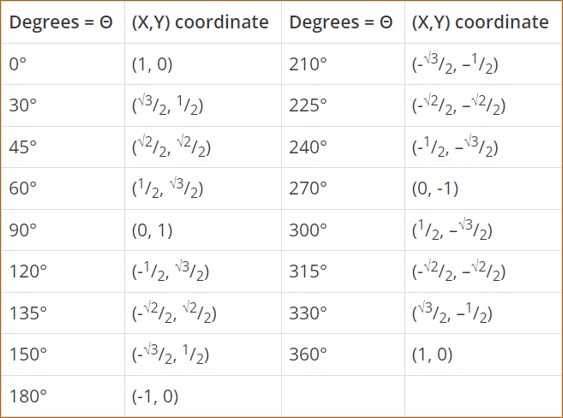
The Unit Circle



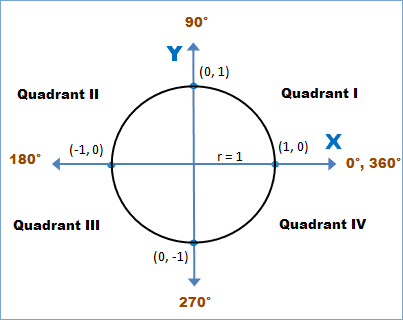This is important to remember when we define the X and Y Coordinates around the Unit Circle. The Unit Circle has 360°. The Unit Circle has 360°. In the above graph, the Unit Circle is divided into 4 Quadrants that split the Unit Circle into 4 equal pieces. Each piece is exactly 90°.

Question: Why is each section / Quadrant equal to 90°?

Answer: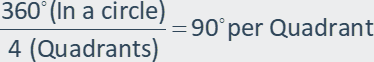

 

 

 

 

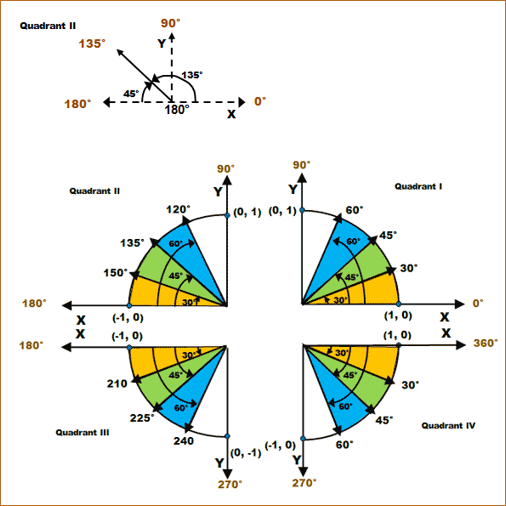The Formula for Calculating Radians is:


 

 

 

 

 

 

 

 

Let’s Practice.
UNIT CIRCLE QUIZ ALL VALUES (purposegames.com)

 

 

 

Converting from Radians and Degrees

 

 

 

 


 

Section Overview

●    Convert radians to degrees.

●    Convert degrees to radians.

●    Solve problems involving degrees and radians.

 

 

Key Vocabulary:

Degree of a Circle - 360 degrees

Radian of a Circle - An angle whose corresponding arc in a circle is equal to the radius of the circle.

 

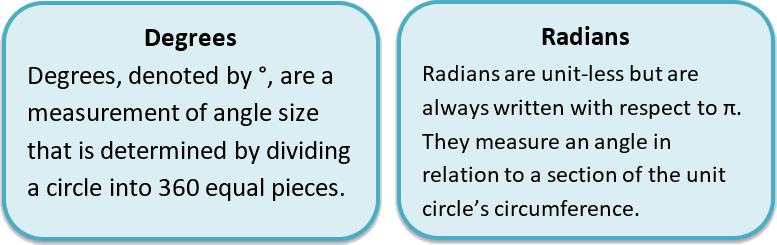
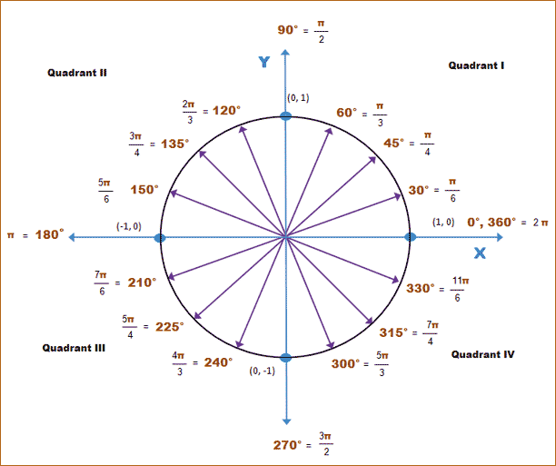
Radian to Degree Measure

The measure of an angle is determined by the amount of rotation from the initial side to the terminal side. In radians, one complete counterclockwise revolution is 2π and in degrees, one complete counterclockwise revolution is 360°.  So, degree measure and radian measure are related by the equations 360° = 2π radians and 180° = π radians

 

From the latter, we obtain the equation 1 radian = .  This leads us to the rule to convert radian measure to degree measure.  To convert from radians to degrees, multiply the radians by  

 

 


Example 1: Convert π/4 radians to degrees.



 

 

 


 

Example 2: Convert 9π/5 radians to degrees.

 

 

 

 

 

 

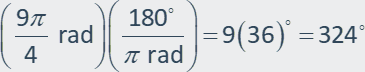
Example 3: Convert 3 radians to degrees.

 

 

 

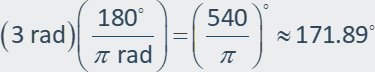
Degree to Radian Measure

The measure of an angle is determined by the amount of rotation from the initial side to the terminal side.  In radians, one complete counterclockwise revolution is 2π and in degrees, one complete counterclockwise revolution is 360°.  So, degree measure and radian measure are related by the equations 360° = 2π radians and 180° = π radians.


From the latter, we obtain the equation 1°= π/180 radians. This leads us to the rule to convert degree measure to radian measure. To convert from degrees to radians, multiply the degrees by π/180° radians.

 

 

 

 

Example 1: Convert 60° to radian measure.


 

 

 

Example 2: Convert 150° to radian measure.

 

 

 

 

 

 


Let’s Practice.