Trig Story Problems and Trig Reciprocals
Trig Story Problems
Section Overview
● Find an unknown angle
measure in a right triangle (given a figure) using the sine, cosine, and
tangent ratios, and their inverse functions.
● Draw a figure from a question
and determine an unknown angle in a right triangle.
● Interpret and solve
real-life and applied problems using right triangle trigonometry.
Key Vocabulary:
Angle of Elevation - The angle between the horizontal and the line of sight to an
object above the horizontal.

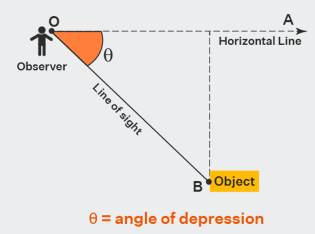
Angle of Depression - The angle between the horizontal and the line of sight to an
object below the horizontal.
What is a Right-Triangle Word Problem?
A right-triangle word problem
is one in which you are given a situation (like measuring somethingís heigh)
that can be modelled by a right triangle. You will draw the triangle,
label it, and then solve it; finally, you interpret this solution within the
context of the original exercise.
Once you've learned about trigonometric ratios (and their inverses), you can
solve triangles. Naturally, many of these triangles will be presented in the
context of word problems. A good first step, after reading the entire exercise,
is to draw a right triangle and try to figure out how to label it. Once you've
got a helpful diagram, the math is usually pretty straightforward.
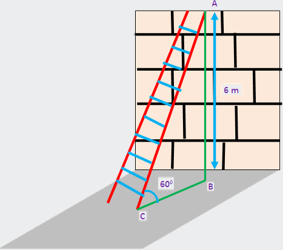
Example 1: A five-meter-long ladder leans against a wall, with the top of
the ladder being four meters above the ground. What is the approximate angle
that the ladder makes with the ground? Round to the nearest whole degree.
As usual, I'll start with a picture, using "alpha" to stand for the
base angle:
 |
They've given me
the "opposite" and the hypotenuse, and asked me for the angle value.
For this, I'll need to use inverse trig ratios.
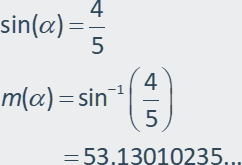 |
(Remember that m(α) means
"the measure of the angle α".)
So, I've got a value for the measure of the base angle. Checking the original
exercise, I see that I am supposed to round to the nearest whole degree, so my
answer is:
base angle: 53į
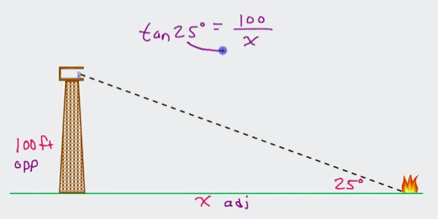
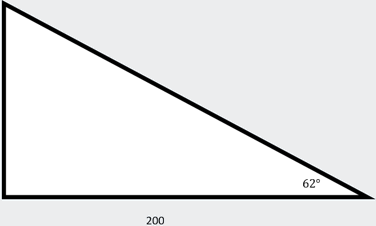
Example 2: While waiting for your sister to finish her bungee jump, you decide
to figure out how tall the platform she is jumping off is. You are standing 200
feet from the base of the platform, and the angle of elevation from your
position to the top of the platform is 62 degrees. How many feet tall is the
platform?
Explanation: You can draw the following right triangle using the
information given by the question:
 |
Since you want to find the height of the platform, you will need to use tangent.
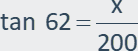 |
| x = 376.15
|
Letís Practice.
Right
triangle trigonometry word problems (practice) | Khan Academy
Trig Reciprocals
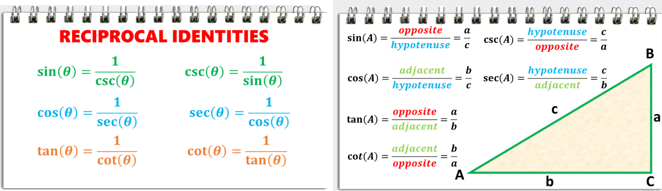
Section Overview
● Solve equations
involving simple reciprocal trigonometric functions (secant, cosecant, and
cotangent).
● Recognize the
periodicity of reciprocal trigonometric functions and use this to determine all
the solutions to a particular equation.
Key Vocabulary:
Cotangent - Ratio of the adjacent to the opposite side of a right-angled
triangle.
Cosecant - Ratio of the hypotenuse to the opposite side of a
right-angled triangle.
Secant - Ratio of the hypotenuse to the adjacent side of a
right-angled triangle.
Weíve
already learned the basic trig ratios:
 |
But there are three more ratios to think about.
 |
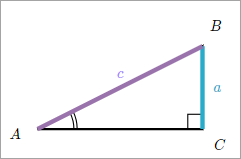
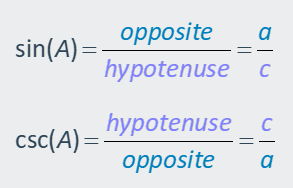
The Cosecant (CSC)
The cosecant is the
reciprocal of the sine. It is the ratio of the hypotenuse to the side opposite
a given angle in a right triangle.
 |
 |
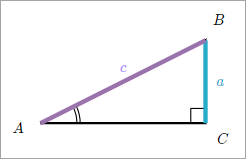
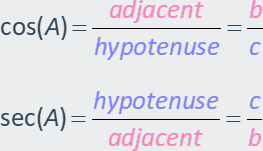
The Secant (sec)
The secant is the reciprocal of
the cosine. It is the ratio of the hypotenuse to the side adjacent to a given
angle in a right triangle.
 |
 |
The Cotangent
(cot)
The cotangent
is the reciprocal of the tangent. It is the ratio of the adjacent side to the
opposite side in a right triangle.
 |
 |
Letís study an
example.
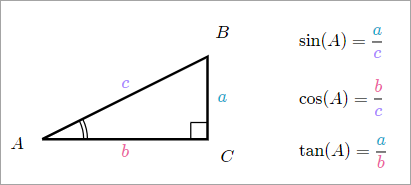
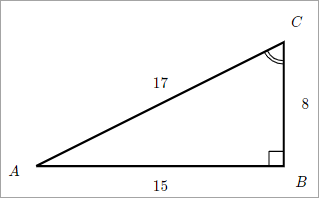
In the triangle below,
find csc(C), sec(C), and cot(C).
 |
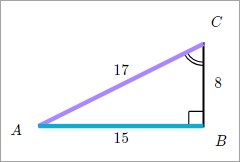
Finding the Cosecant
We know that the cosecant is the reciprocal
of the sine.
 |
 |
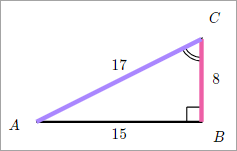
Finding the Secant
We know that the secant is the reciprocal
of the cosine.
 |
 |
Finding the Cotangent
We know that cotangent is the reciprocal
of the tangent.
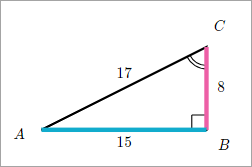 |
 |
Letís Practice.
Reciprocal
trig ratios (practice) | Khan Academy