Transformations of Functions


 

 

Transformation of Functions

 

Section Overview

●    Identify a function reflection given an equation.

●    Identify a function dilation given an equation. 

●    Sketch a graph of a transformed function given the graph of the original function.

 

Key Vocabulary:

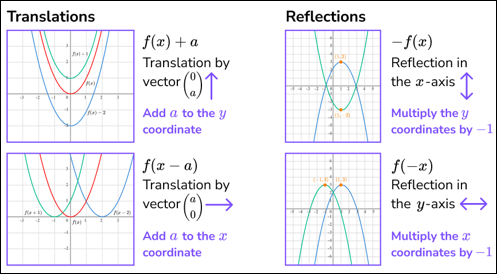
Vertical shift - A transformation of the graph of y = f(x), represented by h(x) = f(x) ± c, in which the graph is shifted upward or downward c units respectively (c is a positive real number).

 

Horizontal shift - A transformation of the graph of y = f(x), represented by h(x) = f(x ± c), in which the graph is shifted to the left or to the right c units respectively (c is a positive real number).

Flip - A transformation of the graph of y = f(x), represented by h(x) = -f(x), in which the graph is flipped over the x-axis. The function is multiplied by -1 to get -f(x).

Nonrigid transformations - A transformation of a graph that cause a distortion—a change in the shape of the graph.

 

The standard form of a quadratic function presents the function in the form:  f (x) = a(x – h)2 + k

“a” Represents Stretching or Compressing

“x” Represents the x-value of a point on the coordinate plane

“h” Represents moving parent function (original) left and right

“k” Represents moving parent function up and down

 

 

 

 

 

 

Shift Up and Down by Changing the Value of k

You can represent a vertical (up, down) shift of the graph of f(x) = x2 by adding or subtracting a constant, k.

 

f(x) = x2 + k

 

If k > 0, the graph shifts upward, whereas if k < 0, the graph shifts downward.

 

Example 1: Determine the equation for the graph of f(x) = x2 that has been shifted up 4 units. Also, determine the equation for the graph of f(x) = x2 that has been shifted down 4 units.

Solution:

The equation for the graph of f(x) = x2 that has been shifted up 4 units is f(x) = x2 + 4.


The equation for the graph of f(x) = x2 that has been shifted down 4 units is f(x) = x2 – 4.

 

 

Shifting Left and Right by Changing Value of h
You can represent a horizontal (left, right) shift of the graph of f(x) = x2 by adding or subtracting a constant, h, to the variable x, before squaring.

f(x) = (x – h)2

If h > 0, the graph shifts toward the right and if h < 0, the graph shifts to the left.


Example 1:

Determine the equation for the graph of f(x) = x2 that has been shifted right 2 units. Also, determine the equation for the graph of f(x) = x2 that has been shifted left 2 units.

Solution:
The equation for the graph of f(x) = x2 that has been shifted right 2 units is f(x) = (x – 2)2.

 

The equation for the graph of f(x) = x2 that has been shifted left 2 units is f(x) = (x + 2)2.

 


Stretching and Compressing by changing the value of a

You can represent a stretch or compression (narrowing, widening) of the graph of f(x) = x2 by multiplying the squared variable by a constant, a.

f(x) = ax2

The magnitude of |a|= ax2 indicates the stretch of the graph. If |a|> 1, the point associated with a particular x-value shifts farther from the -axis, so the graph appears to become narrower, and there is a vertical stretch. But if |a|< 1, the point associated with a particular x-value shifts closer to the x-axis, so the graph appears to become wider, but in fact there is a vertical compression.

 

Determine the equation for the graph of f(x) = x2 that has been compressed vertically by a factor of 1/2. Also, determine the equation for the graph of f(x) = x2 that has been vertically stretched by a factor of 3.

Solution:

The equation for the graph of f(x) = x2 that has been compressed vertically by a factor of 1/2 is f(x) = (½) x2


The equation for the graph of f(x) = x2 that has been vertically stretched by a factor of 3 is f(x) = 3x2.

 

 


 

 

 

 

 

Let’s Practice.

1) The minimum point on the graph of the function y = f(x) is (-2, -4). What is the minimum point on the graph of the function y = f(x) + 7?

 




2) If the graph of the function y = 2x is reflected over the x-axis, the equation of the reflection is ___________.




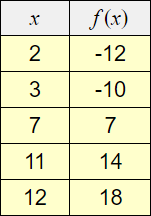
3) Function f(x) is shown in the table below. Which of the choices represents the value of h(3), given that h(x) = f(x) + 4?

 



 

4) Function y = f(x) has been shifted 3 units to the right and 5 units down. Which of the following equations represents these changes?


A) y = f(x + 3) – 5            B) y = f(x – 3) + 5


C) y = f(x + 3) + 5            D)y = f(x – 3) - 5


 

 

5) Which of the following statements describes the transformation indicated by:  f(x) = x2 becomes g(x) = (x – 3)2     

   

A) Function f was translated (shifted) horizontally 3 units to the left.

B) Function f was translated (shifted) vertically 3 units down.

C) Function f was translated (shifted) horizontally 3 units to the right.

D) Function f was translated (shifted) vertically 3 up.





Rotations of Graphs

 

Section Overview

·      Understand the transformations on the coordinates of a point when it is rotated about the origin on the coordinate plane by 90° counterclockwise.

·      Identify equivalent rotations on the coordinate plane.

·      Identify the image of a point, line segment, or shape after a given rotation about the origin.

·      Rotate points, line segments, and shapes about the origin by multiples of 90°.

·      Understand the properties of rotation about a point.

 

Key Vocabulary:

Rotation - A transformation where a figure is turned about a fixed point. Also called a turn.

 

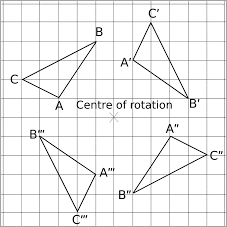
Center of Rotation - A fixed point which shapes move in a circular motion to a new position.



Rotational Symmetry - When a figure can be turned less than 360° about its center and still look like the original.

 

A rotation is a transformation in which a figure is turned around a fixed point, called the center of rotation.

A rotated figures has the same size and shape as the original figure.

The newly rotated figure is called an image of the original figure.

 


 

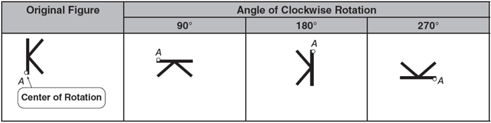
The points of an image on a coordinate grid are labeled with a ′ (prime) following the letter.

Here are the rotation rules:

●    90° clockwise rotation: (x, y) becomes (y, -x)

●    90° counterclockwise rotation: (x, y) becomes (-y, x)

●    180° clockwise and counterclockwise rotation: (x, y) becomes (-x, -y)

●    270° clockwise rotation: (x, y) becomes (-y, x)

●    270° counterclockwise rotation: (x, y) becomes (y, -x)


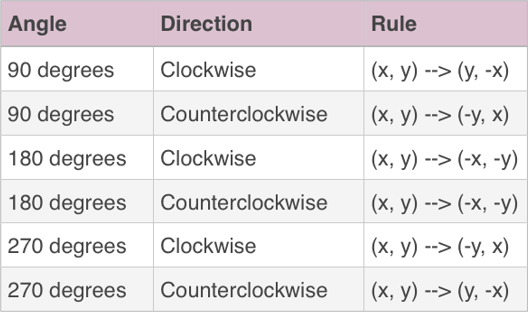
Now that we know how to rotate a point, let’s look at rotating a figure on the coordinate grid. To rotate triangle ABC about the origin 90° clockwise we would follow the rule (x, y) è (y, -x), where the y-value of the original point becomes the new x-value and the x-value of the original point becomes the new y-value with the opposite sign. Let’s apply the rule to the vertices to create the new triangle A′B′C′:

·      A (-4, 7) becomes A′ (7, 4)

·      B (-6, 1) becomes B′ (1, 6)

·      C (-2, 1) becomes C′ (1, 2)

 



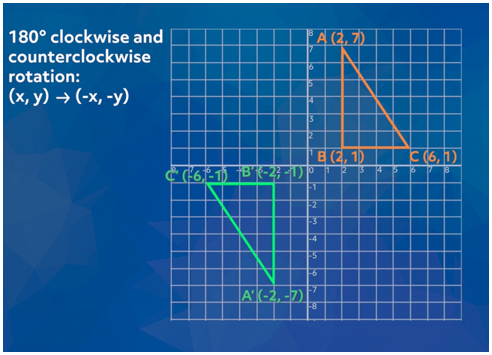
Let’s take a look at another rotation. Let’s rotate triangle ABC 180° about the origin counterclockwise, although, rotating a figure 180° clockwise and counterclockwise uses the same rule, which is (x, y) becomes (-x, -y), where the coordinates of the vertices of the rotated triangle are the coordinates of the original triangle with the opposite sign. Let’s apply the rule to the vertices to create the new triangle A′B′C′:

 

·      A (2, 7) becomes A′ (-2, -7)

·      B (2, 1) becomes B′ (-2, -1)

·      C (6, 1) becomes C′ (-6, -1)



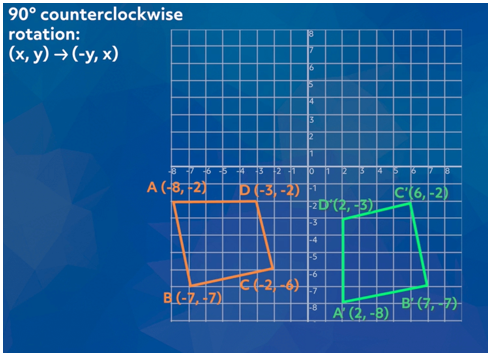
Here is quadrilateral ABCD. To rotate quadrilateral ABCD 90° counterclockwise about the origin we will use the rule (x, y) becomes (-y, x). Let’s apply the rules to the vertices to create quadrilateral A′B′C′D′:

·      A (-8, -2) becomes A′ (2, -8)

·      B (-7, -7) becomes B′ (7, -7)

·      C (-2, -6) becomes C′ (6, -2)

·      D (-3, -2) becomes D′ (2, -3)

 

 

 

 

 


Let’s Practice.

 

Rotate shapes (practice) | Rotations | Khan Academy