Working with Sets
Working with Sets
Section Overview
In this unit, students will be able to
identify collections of numbers, variables, or any other items into categories
called sets.
Key Concepts: Set notation, Numerical Sets, Universal Set, Subsets, and Null
Sets
What
is a set? Well, simply put, it's a
collection.
First,
we specify a common property among "things" (we define this word
later) and then we gather up all the "things" that have this common
property.

For
example, the items you wear: hat, shirt, jacket, pants, and so on.
I'm
sure you could come up with at least a hundred.
This
is known as a set.
Or another example is types of fingers.
|
 |
So, it is just things grouped
together with a certain property in common.
There is a fairly simple
notation for sets. We simply list each element (or "member")
separated by a comma, and then put some curly brackets around the whole thing:
 |
The curly brackets { } are sometimes called "set brackets" or
"braces."
This
is the notation for the two previous examples:
{socks,
shoes, watches, shirts, ...}
{index,
middle, ring, pinky}
Notice
how the first example has the "..." (three dots together).
The three dots ... are called an ellipsis, and mean
"continue on".
So
that means the first example continues on ... for infinity.
So:
●
The first set {socks,
shoes, watches, shirts, ...} we call an infinite set,
● the second set {index, middle, ring, pinky} we call a finite set.
But
sometimes the "..." can be used in the middle to save writing long
lists:
Example 1: the set of letters {a,
b, c, ..., x, y, z}
In this case it is a finite set
(there are only 26 letters, right?)
Numerical Sets
So, what
does this have to do with mathematics? When we define a set, all we have to
specify is a common characteristic. Who says we can't do so with numbers?
Set of even numbers: {..., −4,
−2, 0, 2, 4, ...}
Set of odd numbers: {..., −3, −1, 1, 3, ...}
Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}
Positive multiples of 3 that are less than 10: {3, 6, 9}
And
so on. We can come up with all different types of sets.
We
can also define a set by its properties, such as {x|x>0} which means "the set of
all x's, such that x is greater than 0", see Set-Builder Notation to learn more.
And
we can have sets of numbers that have no common property, they are just defined that way. For example:
{2, 3, 6, 828, 3839, 8827}
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203}
Are
all sets that I just randomly banged on my keyboard to produce.
Universal Set
 |
At
the start we used the word "things" in quotes.
We
call this the universal set. It's a
set that contains everything. Well, not exactly everything. Everything that is relevant
to our question.
|
 |
In Number Theory the universal set is all the integers, as Number Theory is simply the study of integers. |
|
 |
But in Calculus (also known as real analysis), the universal set is almost always the real numbers. |
|
 |
And in complex analysis, you guessed it, the universal set is the complex numbers. |
A =
{a,..
|
When talking about sets, it is
fairly standard to use Capital Letters to represent the set, and lowercase
letters to represent an element in that set.
|
Now
you don't have to listen to the standard, you can use something like m
to represent a set without breaking any mathematical laws (watch out, you can
get π years in math jail for dividing
by 0), but this notation is pretty nice and easy to follow, so why not?
Also,
when we say an element a is in a set
A, we use the symbol ∊ to show it.
And
if something is not in a set use ∉.
Example 1: Set A is {1,2,3}.
We can see that 1 ∈ A, but 5 ∉ A
Subsets
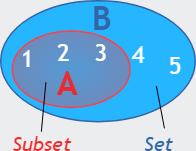
When
we define a set, if we take pieces of that set, we can form what is called a subset.
Example 1: the set {1,
2, 3, 4, 5}
A subset of this is {1, 2, 3}. Another subset is {3, 4} or even
another is {1}, etc.
But {1, 6} is not a subset, since it has an element
(6) which is not in the parent set.
In general:
So, let's use this definition
in some examples.
Example 2: Is A a subset of B, where A = {1,
3, 4} and B = {1, 4, 3, 2}?
1 is in A, and 1 is in B as well. So far so good.
3 is in A and 3 is also in B.
4 is in A, and 4 is in B.
That's all the elements of A,
and every single one is in B, so we're done.
Yes, A is a subset of B
Note that 2 is in B, but 2 is
not in A. But remember, that doesn't matter, we only look at the elements in A.
Let's try a harder example.
Example 3: Let A be all multiples of 4 and B be all multiples of 2.
Is A a
subset of B? And is B a subset of A?
Well, we can't check every
element in these sets, because they have an infinite number of elements. So we need to get an idea of what the elements look like in
each, and then compare them.
The sets are:
A = {..., −8,
−4, 0, 4, 8, ...}
B = {..., −8,
−6, −4, −2, 0, 2, 4, 6, 8, ...}
By pairing off members of the two sets, we can see that every member of A is
also a member of B, but not every member of B is a member of A:
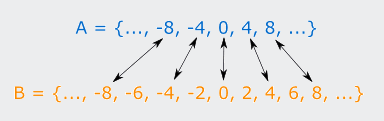
So,
A is a subset of B, but B is not a subset of A.
If we look at the definition of
subsets and let our mind wander a bit, we come to a weird conclusion.
Let A be a set. Is every element of A in A?
Well, umm, yes of course, right?
So that means that A is a
subset of A. It is a subset of itself!
A is a proper subset of
B if and only if every element of A is also in B, and there exists at least
one element in B that is not in A.
This little piece at the end is there to make sure that A is not a proper
subset of itself: we say that B must have at least one extra element.
Example 1: {1, 2, 3} is
a subset of {1, 2, 3}, but is not a proper subset of {1, 2, 3}.
Example 2: {1, 2, 3} is a proper subset of {1, 2, 3, 4} because the
element 4 is not in the first set.
Notice that when A is a proper subset of B then it is also a subset of B.
When we say that A is a subset
of B, we write A ⊆ B.
Or we can say that A is not a subset of B by A ⊈ B ("A is not a subset of B")
When we talk about proper subsets, we take out the line underneath and so it
becomes A ⊂
B or if we want to say the opposite, A ⊈ B.
Empty (or Null) Set
This is probably the weirdest
thing about sets.

As an example, think of the set of piano keys on a guitar.
"But wait!" you say, "There are no piano keys on a guitar!"
And right you are. It is a set with no elements.
This is known as the Empty Set (or Null Set). There aren't any elements
in it. Not one. Zero.
It is represented by ∅.
Or by { } (a set with no elements)
Some other examples of the empty set are the set of countries south of the
south pole.
Letís Practice.
1) Which
of the following is sets is shown with roster notation?

 |
2) Which
of the following is true about set D listed below?
D = {-3, -2, -1, 0, 1, 2, 3}
A) -7
∈ D
B) -2
∈ D
C) D is an infinite set.
D) All of the above.
 |
3) Which
of the following is an infinite set?

 |
4) Which
of the following sets is equal to the set listed below?
X = {2, 3, 5, 7, 11, 13, 17, 19}
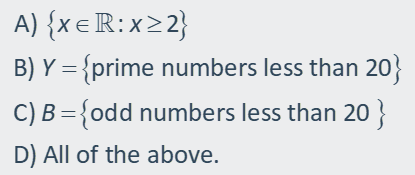
 |
5) Which
of the following sets is equal to the set listed below?
X = {2, 3, 5, 7, 11, 13, 17, 19}

 |
6) If
A = {types of triangles} and B = {types of trapezoids}, then which of the
following is the universal set?
A) ∪ = {polygons}
B) ∪ =
{quadrilaterals}
C) ∪ =
{hexagons}
D) All of the above.
 |
7) Which
of the following is the correct set-builder notation for the set listed below?
{-5,
-4, -3, -2, -1, 0, 1, 2, 3, ...}
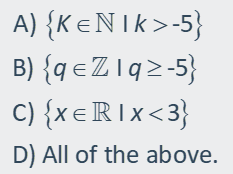
 |
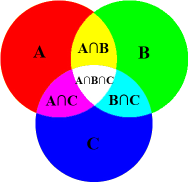
8) In
the Venn diagram below, U = {students who attend The Smart School}, then
which of the following is the complement of set A?

A) A' = {students who do not attend The
Smart School}
B)
A' = {students who attend the Not So Smart School}
C) A' = {students who do not take the bus to school}
D)
None of the above.
 |
9) Which
of the following is represented by the shaded region in the Venn diagram below?
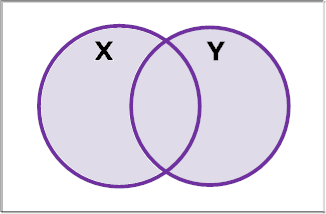
A) X ∪ Y
B)
X ∩ Y
C) X'
D)
All of the above.
 |
10) Which
of the following is represented by the shaded region in the Venn diagram below?
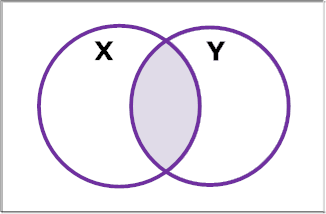
A) X
∪ Y
B)
X ∩ Y
C) X'
D)
All of the above.
 |
Classifying Numbers
Section Overview
Students will also be able to
classify numbers into more distinct categories (irrational, rational, integer, whole,
and counting)

Key Concepts: Understanding the differences between the classifying categories:
How can we classify a Real
Number?
When we first start to work with numbers, we generally count on
our fingers or count any number of physical objects placed in front of us.

To perform these actions, we
involve a set of numbers known as the counting numbers or the natural numbers.
The natural numbers are used to count a number of objects. This set begins with
the number one and increases in increments of one out to positive infinity.
Natural Numbers: {1, 2, 3, 4,...}
Note:
The three dots "..." after the 4 in our set are used to indicate that
the pattern continues forever. After 4 comes 5, then 6, so on and so forth...
We can also use a number line to visually display our set of natural numbers.
The leftmost number is a 1 and then each additional notch on the number line is
shown as an increase of 1 or the next natural number. Since we can't list all
of the numbers, we draw an arrow to the right to indicate the natural numbers
continue out to positive infinity.
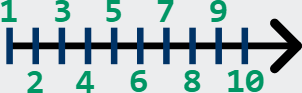
As we move on, we begin to
consider the possibility of not having anything to count. This is represented
with the number 0. When 0 is added to the set of natural numbers, we end up
with the whole numbers.
Whole Numbers: {0, 1, 2, 3, 4,...}
In some cases, it is not enough to have only the whole numbers.
What if we need to describe a temperature that is less than zero, an altitude
that is below sea level, or a negative bank balance? To deal with these
situations, we can introduce the integers. These are the whole numbers and
their opposites or negatives. To form this set, we just take the whole numbers
and then working to the left of zero, we start counting from 1 again, only this
time we place a negative symbol in front of the number.

Integers: {..., -4, -3, -2, -1, 0, 1, 2,
3, 4,...}
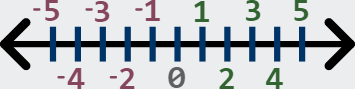
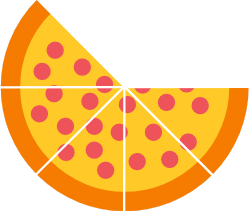
Additionally, we may have a situation in which we don't have a
whole amount. Suppose we eat 3 slices of pizza out of a total of 8 slices that
are available. Currently, we have more pizza than zero and less than one whole
pizza. We can use a fraction such as 5/8 to describe the amount of pizza that
is remaining or another fraction 3/8 to describe the amount of pizza that was
eaten. This type of number is known as a rational number. A rational number can
be written as the quotient of two integers with a nonzero divisor
(denominator). In decimal form, a rational number will always terminate or
repeat the same pattern of digits forever. For example, in decimal form: 9/11
is 0.818181..., where the 81 repeats forever.
![]()
Note
the bar over the digits 81, indicate the pattern continues forever...
Rational Numbers: {p/q
| p and q are integers and q ≠ 0}
Lastly, we have the irrational numbers. These are real numbers
that don't fall in the category of being a rational number. This means we can't
write an irrational number as the quotient of two integers. When we see an
irrational number in decimal form, the number will not terminate nor repeat the
same pattern forever. The most famous example of an irrational number is pi,
which is the ratio of a circle's circumference to its diameter. When we need to
work with pi, we generally give an approximation of 3.14159, but after the 9
comes an infinite number of digits.
Irrational Numbers: {x | x is
a real number but is not rational}
Together, the rational numbers and irrational numbers make up all of the real
numbers. Therefore, if we are dealing with a real number, it must be either
rational or irrational.
Letís Practice.
1) How can we classify the given number?
a) -2
b) ![]()
 |
2) How can we classify
the given number?
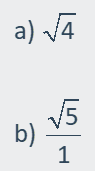
 |
3) How can we classify
the given number?
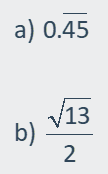
 |
4) Determine which of the following numbers are Whole Numbers.
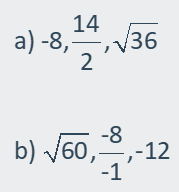
 |
5) Determine which of
the following numbers are Irrational Numbers.

 |