Rewriting Equations and Formulas

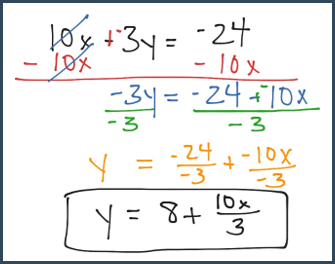
Unit Objective

● Solve literal equations for given variables

Key Vocabulary

● Literal equation - an equation that has 2 or more variables.

● To rewrite a literal equation, solve for one variable in terms of the other variable

Let's Practice.

Which of the following is a literal equation?

2x – 14.5 = 70.3 or 6x + 3y = 90

---

Rewriting an Equation

Example 1: Solve the equation 2y + 5x = 6 for y.

2y + 5x = 6 Write the equation.

2y + 5x – 5x = 6 – 5x Subtraction Property of Equality

2y = 6 – 5x Simplify.

Division Property of Equality

Simplify.

Let's practice.
Solve the equations for y.

1) 5y – x =10 2) 4x – 4y =1 3) 12 = 6x + 3y

---

Rewriting a Formula

Example 1: The formula for the surface area S of a cone is S = πr² + πrl. Solve the formula for the slant height l.

S = πr^2 + πrl. Write the formula. S – πr^2= πr^2 – πr^2+ πrl Subtraction Property of Equality S – πr^2= πrl Simplify. Division Property of Equality Simplify.

Let's practice.

Solve the formula for the red variable.

1) Area of a rectangle: A = bh

2) Simple interest: I = Prt

3) Surface area of cylinder: S = 2πr ² + 2πrh

---

Rewriting that Temperature Formula
A formula for converting from degrees Fahrenheit F to degrees Celsius C is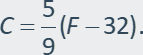

Example 1: Solve the temperature formula for F.

Write the temperature formula.

Multiplication Property of Equality

Simplify.

. Addition Property of Equality

Simplify.

The rewritten formula is

Let’s Practice.

Solve the formula for C.

---

Modeling in Real Life

Example 1: Which has the greater temperature?

Understand the Problem

You are given the temperature of the Sun in degrees Fahrenheit and the temperature of lightning in degrees Celsius. You are asked which temperature is greater.

Make a Plan
Convert the Celsius temperature to Fahrenheit. Then compare the temperatures.

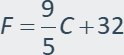
Solve and Check

Write the formula.

Substitute 30,000 for C.


= 54,032 Simplify.

Because 54,032°F > 11,000 °F, lightning has the greater temperature.