Comparing Populations

Unit Objective

● Comparing populations using measures of center and variation.

● Measures of center- mean, median, Interquartile range, and mean Absolute deviation (MAD).

Key Vocabulary

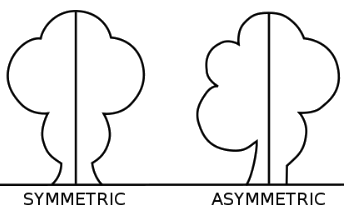
· Symmetric - the same on both sides of the center

· Asymmetric means not symmetric

· Skewed - more to one side of center

Box-and-Whisker Plot

Mean Absolute Deviation(MAD)

---

Comparing Populations

Use the mean and the mean absolute deviation (MAD) to compare populations when both distributions are symmetric.

Use the median and the Interquartile range (IQR) when one or both distributions are skewed.

In the following example (example 1) the distributions are skewed. Therefore, we use median and IQR.

Example 1: Two data sets contain an equal number of values. The double box-and-whisker plot represents the values in the data sets.

a) Compare the data sets using measures of center and variation.

Both distributions are skewed. Use the median and the IQR.

Data set A	Data set B
Median = 60	Median = 90
IQR = 80 – 30 = 50	IQR = 100 – 80 = 20

So, Data set B has a greater measure of center, and Data set A has a greater measure of variation.

b) Which data set is more likely to contain a value of 95?

About 25% of the data values in Data set A are between 80 and 130.

About 50% of the data values in Data set B are between 80 and 100.

So, Data set B is more likely to contain a value of 95.

c) Which data set is more likely to contain a value that differs from the center by at least 30?

The IQR of Data set A is 50 and the IQR of Data set B is 20. This means it is more common for a value to differ from the center by 30 in Data set A than in Data set B.

So, Data set A is more likely to contain a value that differs from the center by at least 30.

Let's practice.

1) Which data set is more likely to contain a value of 70?

2) Which data set is more likely to contain a value that differs from center by no more than three?

---

Describing Visual Overlap

When two populations have similar variabilities, the visual overlap of the data can be described by writing the differences in the measures of center (mean, median) as a multiple of s measure of variation (MAD).

Example 1: The double dot plot shows two data sets. Express the difference in the measures of center as a multiple of the measure of variation.

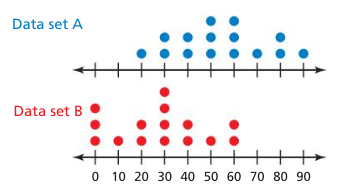Both distributions are approximately symmetric. Use the mean and the MAD to describe the centers and vartaions.

So, the difference in the means is about 1.6 times the MAD.

Let's practice.

WHAT IF? Each value in the dot plot for Data set A increased by 30. How does this affect your answers. Explain.

When the difference in measures of center is at least two times the measure of variation, the difference is significant.

---

Modeling Real Life

The double box-and-whicker plot represents the heights of rollercoasters at two amusement parks. Are the rollercoasters significantly taller at one part than at the other park?

The distribution for Park A is skewed, so use the median and the IQR to describe centers and variations.

Park A	Park B
Median = 50	Median = 55
IQR = 55 – 45 = 10	IQR = 60 – 50 = 10

Because the variabilities are similar, you can describe the visual overlap by expressing the difference in the medians as a multiple of the IQR.

Because the quotient is less than 2, the difference in the medians is not significant.

The rollercoasters are not significantly taller at one park than at the other park.

Let’s Practice.
The double box-and-whisker plot represents the weights of cats at two shelters. Are the cats significantly heavier at one shelter than at the other? Explain.