Decimals in Real Life

Unit Objective

● Use decimals to solve everyday problems

Key Vocabulary

● A decimal is another way to write a fraction. You can think of a decimal as a part of a whole number. It is less than 1 whole thing, but more than 0.

● You may not realize it, but you see decimals a lot in real life. One of the most common examples is money.

● The following is the process to convert a fraction to a decimal and round it when necessary

Let's Practice.

Convert 3/7 to a decimal and round to the nearest 100th.

The following is the process to convert a decimal to a fraction.

Let’s Practice.
Write 2.85 as a mixed number.

Adding and Subtracting Decimals

To add or subtract decimals, write the numbers vertically and line up the decimal points. Then bring down the decimal point and add or subtract as you would with whole numbers.

Example 1: Adding Decimals

a) Add 8.13 + 2.76. Estimate 8 + 3 = 11

8.13

+ 2.76 Add as you would with whole numbers.

10.89 Reasonable? 10.89 » 11 ü

b) Add 1.459 + 23.7.

1.459

+ 23.700 Insert zeros so that both numbers have the same

25.159 number of decimal places.

Example 2: Subtracting Decimals

a) Subtract 5.508 – 3.174. Estimate 6 – 3 = 3
4 10

– 3.174 Subtract as you would with whole numbers.

2.334 Reasonable? 2.334 » 3 ü

b) Subtract 21.9 – 1.605.

– 1.605 Insert zeros so that both numbers have the same

20.295 number of decimal places.

Let's practice.

Gabby bought milk shakes for her 4 friends. It costs her $24.34. She paid with a 20 and a 10 dollar bill. How much change did she receive?

Multiplying Decimals

Multiplying Decimals by Whole Numbers

Words
Multiply as you would with whole numbers. Then count the number of decimal places in the decimal factor. The product has the same number of decimal places.

Numbers

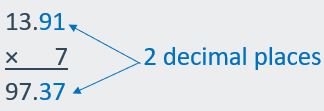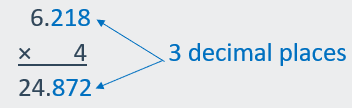Multiplying Decimals by Decimals

Words
Multiply as you would with whole numbers. Then add the number of decimal places in the factors. The sum is the number of decimal places in the product.

Numbers

Let's practice.

Calculate sale tax of 7% on a purchase of $48.75.

Dividing Decimals

a) Find 18.2 ÷ 1.4.

So, 18.2 ÷ 1.4 = 13.

Check 13 × 1.4 = 18.2 ü

b) Find 0.273 ÷ 0.39.

So, 0.273 ÷ 0.39 = 0.7.

Check 0.7 × 0.39 = 0.273 ü

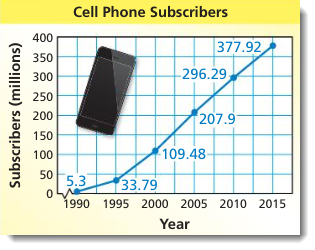
Modeling in Real Life

How many times more cell phone subscribers were there in 2015 than in 1990? Round to the nearest whole number.

Divide the number of subscribers in 2015 by the number of subscribers in 1990.

From the graph, there were 377.92 million subscribers in 2015 and 5.3 million in 1990. So, divide 377.92 by 5.3

So, there were about 71 times more subscribers in 2015 than in 1990.

Let’s practice.

You drive 14.63 miles to school. On a certain day it took you 0.3 hours to get to school. What is your average rate of speed? Round to the nearest whole number.