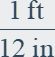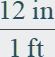Converting Measures


 

Unit Objective

●    Use ratio reasoning to convert units of measure

 

Key Vocabulary

●    Conversion factor - a number or formula used to convert a measurement in one set of units to the same measurement in another set of units

●    Example: to convert feet to inches multiply by 12( the conversion factor).

●    Unit analysis - using the rules of multiplying and reducing fractions to solve problems involving different units

 

 

Example:

 

 

 

 

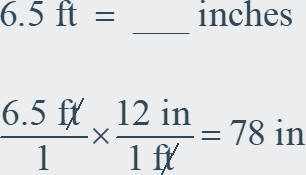
The following reference sheet can be used for many conversions.

 

Mathematics Reference Sheet

 

U.S. Customary

1 foot = 12 inches

1 yard = 3 feet

1 mile = 5280 feet

1 acre = 43,560 square feet

1 cup = 8 fluid ounces

1 pint = 2 cups

1 quart = 2 pints

1 gallon = 4 quarts

1 gallon = 231 cubic inches

1 ton = 2000 pounds

1 cubic foot ≈ 7.5 gallons

 

U.S. Customary to Metric

1 inch = 2.54 centimeters

1 foot ≈ 0.3 meter

1 mile ≈ 1.61 kilometers

1 quart ≈ 0.95 liter

1 gallon ≈ 3.79 liters

1 cup ≈ 237 milliliters

1 pound ≈ 0.45 kilogram

1 ounce ≈ 28.3 grams

1 gallon ≈ 3785 cubic centimeters

Time

1 minute = 60 seconds

1 hour = 60 minutes

1 hour = 3600 seconds

1 year = 52 weeks

 

 

Metric

1 centimeter = 10 millimeters

1 meter = 100 centimeters

1 kilometer = 1000 meters

1 kiloliter = 1000 liters

1 milliliter = 1 cubic centimeter

1 liter = 1000 cubic centimeters

1 cubic millimeter = 0.001 milliliter

1 gram = 1000 milligrams

1 kilogram = 1000 grams

 

Metric to U.S. Customary

1 centimeter ≈ 0.39 inch

1 meter ≈ 3.28 feet

1 kilometer ≈ 0.62 mile

1 liter ≈ 1.06 quarts

1 liter ≈ 0.26 gallon

1 kilogram ≈ 2.2 pounds

1 gram ≈ 0.035 ounce

1 cubic meter ≈ 264 gallons

 

Temperature
C = 5/9(F – 32)

F = 9/5(C + 32)

 

 

 

Metric

The U.S. customary system is a system of measurement that contains units for length, capacity, and weight. The metric system is a decimal system of measurement, based on powers of 10, that contains units for length, capacity, and mass.

You can use unit rates and ratio tables to convert measures within the same system and between systems.

 

 

 


Converting Measures withing the Same System

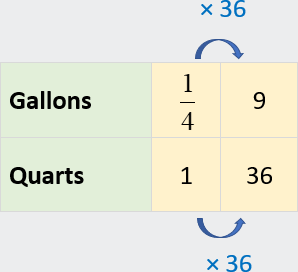
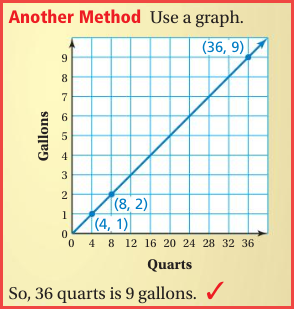
Example: Convert 36 quarts to gallons.
Because 1 gallon = 4 quarts, there are 4 quarts per gallon and ¼ gallon per quart. You can use either of these unit ratios to find an equivalent rate with 36 quarts.

Method 1: Create a ratio table using the unit rate 4 quarts per gallon. Multiply each quantity by 9 to find the number of gallons in 36 quarts.

 


So, 36 quarts is 9 gallons.

 

 

Method 2: Create a ratio table using the unit rate ¼ gallon per quart. Multiply each quantity by 36 to find the number of gallons in 36 quarts.



So, 36 quarts is 9 gallons.


 

Let's Practice.

1) Convert 48 feet to yards.

 


 

Converting Measures Between Systems

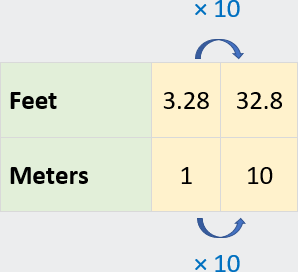
Example: Convert 10 meters to feet.

Because 1 meter ≈ 3.28 feet, there are about 3.28 feet per meter. Because 1 foot ≈ 0.3 meter, there is about 0.3 meter per foot. You can use either of these unit rates to find an equivalent rate with 10 meters.

 

Method 1: Create a ratio table using the unit rate 3.28 feet per meter.

 

 

So, 10 meters is about 32.8 feet.

 

 

Method 2: Create a ratio table using the unit rate 0.3 meter per foot.

 

 

So, 10 meters is about 10/0.3 ≈ 33.33 feet.

 

 

 

Let’s Practice.

1) Convert 7 miles to kilometers. Round to the nearest hundredth is necessary.

 

 

 

 

 

 

Conversion Factor

A conversion factor is a rate in which the two quantities are equal. When using conversion factors, write rates using fraction notation.

                               

  Relationship Conversion Factors
Example: 1 ft = 12 in

 

1 ft per 12 in, or


12 in per 1 ft, or

 

 

You can use unit analysis to decide which conversion factor will product the appropriate units. You can “cross out” a unit that appears in both a numerator and denominator of a product.

 

In the following video, when it pauses you must answer the question and click continue in order to play the rest.

 

 

 

 

Using Conversion Factors
Example: Convert 4 pounds to kilograms.


Use a conversion factor.

1 lb ≈ 0.45 kg

 

 

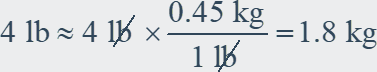
So, 4 pounds is about 1.8 kilograms


Example: Convert 5 yards per second to yards per minute.

Write 5 yards per second as a fraction. Then use a conversion factor.


1 min = 60 sec

 

 

 

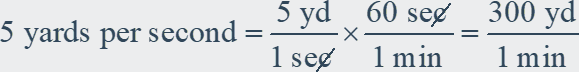
So, 5 yards per second is 300 yards per minute.

 

 

Let's practice.

1) Convert 20 quarts to liters. Round to the nearest hundredth if necessary.

 

 

2) Convert 60 kilometers per hour to miles per hour. Round to the nearest 100th if necessary.

 

 

 

   

 

 

Modeling in Real Life

Example: A runner’s goal is to complete a mile in 4 minutes or less. The runner’s speed is 20 feet per second. Does the runner meet the goal? If not, how much faster (in feet per second) must the runner be to meet the goal?

To meet the goal, the runner must complete 1 mile in 4 minutes or less. The minimum speed required is 1 mile per 4 minutes.


To compare this speed to the runner’s speed of 20 feet per second, convert the minimum speed of 1 mile per 4 minutes to feet per second.

 

So, the runner did not meet the goal because a speed of 20 feet per second is below the minimum speed of 22 feet per second. The runner must be 22 – 20 = 2 feet per second faster to meet the goal.

 

Check: Verify the distances traveled in 4 minutes at the runner’s speed and in 4 minutes at the additional speed have a sum of 1 mile.

 

 

At runner’s speed At additional speed


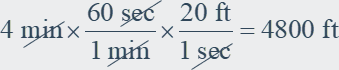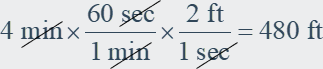The sum of the distances is 4800 + 480 = 5280 feet, or 1 mile.

 

 

Let's practice.

1) A race car driver’s goal it to complete a 1000-kilometer auto race in 4 hours or less. The driver’s average speed is 4200 meters per minute. Does the driver meet the goal? If not, how much faster (in meters per minute) must the driver be to meet the goal?

 

 

 

 

 

 

Metric Conversions

The following video presents an alternative and quick way of doing metric conversions.


When the video stops, answer the question and click continue to continue viewing.