Translations

Unit Overview

In this unit, students will be able to:

· Create translations of geometric figures

· Identify corresponding parts of translated images

Key Concepts

· Rigid transformations

· Translations

Ohio’s Learning Standards

· 8.G.1 Verify experimentally the properties of rotations, reflections, and translations (include examples both with and without coordinates).

o 8.G.1a. Lines are taken to lines, and line segments are taken to line segments of the same length.

o 8.G.1b. Angles are taken to angles of the same measure.

o 8.G.1c. Parallel lines are taken to parallel lines.

· 8.G.2 Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them. (Include examples both with and without coordinates.)

· 8.G.3 Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.

Calculators

· Here is a link to the Desmos scientific calculator that is provided for the Ohio State Test for 8^th Grade Mathematics in the spring.

· You are strongly encouraged to use the Texas Instruments TI-30XIIS handheld scientific calculator. It is extremely user friendly.

Translation:

· a rigid transformation where you slide the image horizontally and vertically

o the image maintains its orientation → it does not turn or flip

Example A: Translate pre-image rABC down 5 units and right 7 units

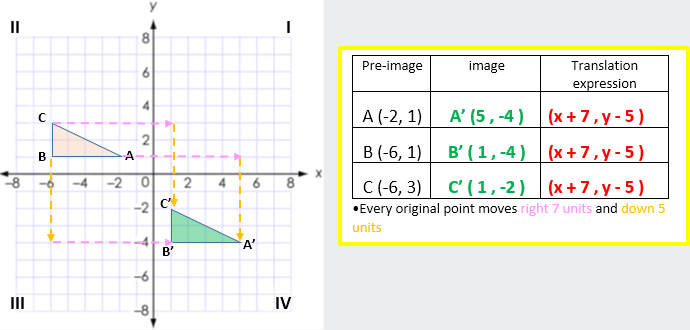· If it helps, you can physically trace a shape (also mark the origin) and slide the tracing paper to see the location of the new image

o Wax paper (burger ‘patty paper’) is great to use

· Like reflections in the previous unit, and any rigid transformation,

o corresponding sides are congruent

o corresponding angles are congruent

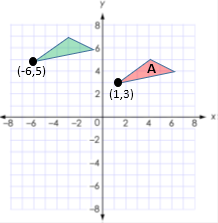
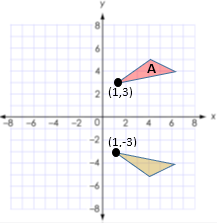
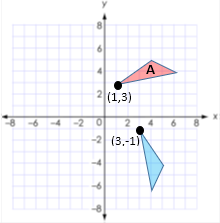
Example B Set: Identify each rigid transformation of triangle A as a reflection, rotation, or translation:

SLIDE → Translation Left 7 units, up 2 units (1, 3) → (-6, 5) (x, y) → (x – 7, y + 2)	FLIP → Reflection reflect over x-axis (1, 3) → (1, -3) (x, y) → (x, -y)	TURN → Rotation rotate 90° clockwise (about the origin) (1, 3) → (3, -1) (x, y) → (y, -x)

Example B Set: Identify each rigid transformation of square ABCD as a reflection, rotation, or translation:

	ABCD → EFGH Corresponding letters: slide over TRANSLATION	ABCD → IJKL Corresponding letters: flipped horizontal              REFLECTION	ABCD → MNOP Corresponding letters: turned 90° clockwise ROTATION

For further explanation and practice on translations:

Let’s Practice:

Use the image below for the following questions:
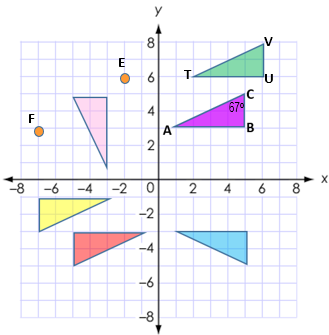