Rational vs.
Irrational Numbers
Unit Overview
In this unit, students will be able
to:
·
Differentiate
different number sets
·
Solve square
root and cube root equations
Key Concepts
·
Real numbers
·
Rational
numbers
·
Irrational
numbers
·
Integers
·
Whole numbers
·
Radicals
Ohio’s Learning Standards
·
8.NS.1 Know that real numbers are either rational or
irrational. Understand informally that every number has a decimal expansion
which is repeating, terminating, or is non-repeating and non-terminating.
·
8.NS.2 Use rational approximations of irrational numbers to
compare the size of irrational numbers, locate them approximately on a number
line diagram, and estimate the value of expressions, e.g., π². For
example, by truncating the decimal expansion of √2, show that √2 is
between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to
get better approximations.
·
8.EE.2 Use square root and cube root symbols to represent
solutions to equations of the form x² = p and x³ = p, where p is a positive
rational number. Evaluate square roots of small perfect squares and cube roots
of small perfect cubes. Know that √2 is irrational.
Calculators
·
Here is a link
to the Desmos scientific calculator that is provided for the Ohio State
Test for 8th Grade Mathematics in the spring.
·
You are
strongly encouraged to use the Texas Instruments TI-30XIIS handheld scientific
calculator. It is extremely user
friendly.
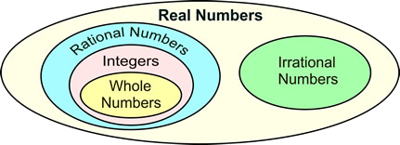
Number sets
·
As stated in the previous unit, real
numbers are broken into two subsets:
 |
·
Rational numbers have two subsets that
we will examine:
o Whole
numbers:
0, 1, 2, 3,…
o Integers: whole
numbers and their opposites
§ …, -3, -2, 1, 0, 1, 2, 3,…
§ The set of whole numbers is a subset (belongs to) the
set of integers
·
All whole #s are integers, but not all
integers are whole numbers
 |
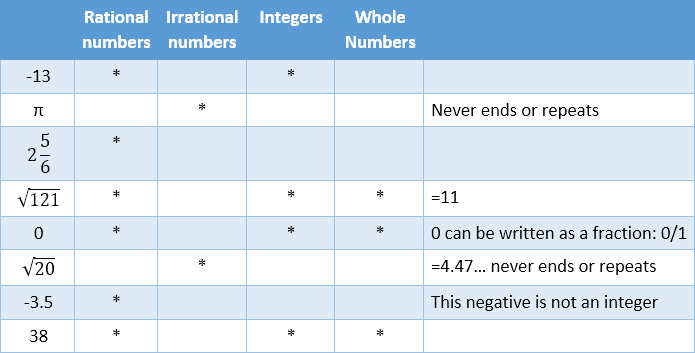
· Example A set: Which sets does the number belong to?
Here are the answers with a few notes:
 |
For further
explanation and practice on number sets:
Let’s practice classifying numbers into what sets that they belong to.
Solving Square Root Equations
In Unit 3, we learned that a key step to solve
most any algebraic equation is the property
of equality, which allows one to perform the same operation to both sides
of equation. This method is used to get
the variable by itself on one side of the equation by eliminating constants and
coefficients. Use the inverse operation to eliminate those numbers.
·
Addition is the inverse operation of subtraction
·
Multiplication is the inverse operation of division
Example B set: Look at these basic examples that illustrate the
four Properties of Equality:
x + 4 = 6 c – 5 = 8 ![]() 6h = -18
6h = -18
x + 4 – 4 =
6 – 4 c – 5 +
5 = 6 + 5
![]() 6h ÷ 6 = -18 ÷ 6
6h ÷ 6 = -18 ÷ 6
x = 2 c
= 11 y
= 48 h =
3
This same
principle can be applied to solve root equations:
·
Finding the square root is
the inverse operation of finding the square
·
Finding the cube root is
the inverse operation of finding the cube
Example C:
x2 = 9 → You probably know that 32
= 9, but remember that (-3)2 = 9
as well.
The solutions are x
= 3 or x = -3 → this can also be written as x = ±3
·
To solve a basic equation involving a square:
o
Take the square root of both sides to
undo the square
o
Also include the ± symbol when
taking the square root to include both solutions
x2 = 9
![]()
x = ±3 → 32
= 3 • 3 =
9 and (-3)2
= (-3) • (-3)
= 9
Example D set: Solving basic x2 (quadratic)
equations
x2 = 36 v2 + 8 =
10.56 5c2
= 100 n2 = -81
![]() -8 -8 ÷5 ÷5
-8 -8 ÷5 ÷5 ![]()
x = ±6 v2 = 2.56 c2 = 20 n = no
solutions
![]()
![]()
v = ±1.4 c = ±4.47 (rounded)
c = ±![]() (exact)
(exact)
Example E set: Solving basic x3 (cubic) equations
x3 = 8 → You may know that 23
= 2•2•2 = 8
(-2)• (-2)•(-2) = -8 →-2 is not a solution for x3
= 8
·
To solve a basic equation involving a cube:
o
Take the cube root of both sides to
undo the square → there is only 1
solution
x3 = 64 c3 = -8 n3 = -100
![]()
![]()
![]()
x = 4
c = -2 n = -4.64 (rounded)
n
= ![]() (exact)
(exact)
For further
explanation and practice on solving root equations:
Let’s practice.