Scientific
Notation
Unit Overview
In this unit, students will be able
to:
·
Identify
numbers in scientific notation
·
Convert
numbers between scientific notation and standard form
·
Perform
operations with scientific notation, including word problems
Key Concepts
·
Scientific
notation
·
Standard form
·
Calculator
form
Ohios Learning Standards
·
8.EE.3 Use numbers expressed in the form of a single digit
times an integer power of 10 to estimate very large or very small quantities
and to express how many times as much one is than the other. For example,
estimate the population of the United States as 3 Χ 108; and the
population of the world as 7 Χ 109; and determine that the world
population is more than 20 times larger.
Calculators
·
Here is a link
to the Desmos
scientific calculator that is
provided for ·
You are
strongly encouraged to use the Texas Instruments TI-30XIIS o
We will be
referring to several functions of this specific calculator at times in this and
other units. Scientific Notation ·
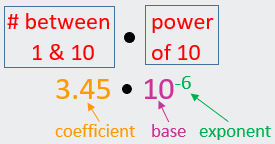
A way of expressing a number,
particularly extremely large or small numbers commonly seen with science topics ·
A number written in scientific notation
must follow this form:
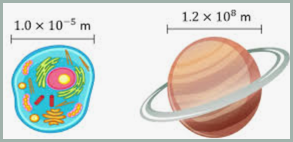
Example A Set → Real life science
numbers Mass of Earth: 5,980,000,000,000,000,000,000,000 kg = 5.98
1024 kg Mass of an oxygen
atom: 0.00000000000000000000000002657 kg = 2.657
10-26 kg Example B Set → numbers not in scientific notation Converting a number
from standard (decimal) form to scientific notation Example C Set: 2nd:
deterimine the exponent by counting how
many place values the decimal moves from the original
decimal point to the new decimal point. ·
Big numbers greater than 1 (where the decimal is moved left) have positive
exponents ·
Small numbers less than 1 (where the decimal is moved right)
have negative
exponents
·
Heres why moving decimal point determines the
exponent → you
are basically multiplying or dividing by a power of 10
Converting a number
from scientific notation to standard (decimal) form Move
the decimal as many places as the exponent value ·
Positive exponents represent big numbers greater
than 1 → move decimal to the right
·
Negative exponents
represent small numbers less than 1 → move decimal to the left
Example D Set → re-write in standard form (normal #s) 8 103 → move right 3 places → 4.321 105 → move right 5 places→ 1.5 x 10-2 → move left 2 places → 8.321 x 10-4ΰ move left 4 places → TI-30XIIS
handheld scientific calculator has a great tool for scientific notation.
Click on the words SCIENTIFIC NOTATION for further
explanation: Lets
Practice: Operations with Scientific Notation ·
Carefully use your scientific calculator
to work out. ·
Use parentheses as needed. ·
Be sure to give the answer in the number
form that is requested (scientific notation or
standard form) Example E Set → ·
2.3 105 + 2.5 102
= 2.3025 105
= 230,250
·
8.4 105 – 5.56 104 = 7.844 105
= 784,400
·
(4 107)(8
10-2) = 3.2 106
= 3,200,000 ·
(3.6 10-2)3 = 4.6656 10-5
= 0.000046656
Example F Set → Fractions and
division can be tricky ·
·
A mistake is to enter this problem in
your calculator as 64/23. o The calculator
follows the order of operations (multiply or divide from left to right): § 64/23 = 24/23=123=36 ·
To do enter this fraction correctly in
your calculator, you either need to o work out the
numerator and denominator separately, then divide those answers (see original
problem above) o OR put both the
numerator and denominator in separate parentheses § (64) / (23) =24/6 = 4 ·
The same principle of using parentheses applies when scientific notation
numbers are divided using the calculator.
o o If you dont use ( ) with this problem, you will get an incorrect answer: 1.4 x 108 Calculator
Notation ·
This is an optional short-cut for typing
numbers in scientific notation o There are
less buttons to push o You do not
ever need to use parentheses for numbers type in calculator form 2.5 102
= 2.5E2 Example E
and F Set re-written in calculator form ·
2.3 105 + 2.5 102 → 2.3E5+2.5E2 ·
(4 107)(8
10-2) → 4E5 8E-2 ·
(3.6 10-2)3 → 3.6E2^3
· Scientific Notation Word Problems Example G Set → make the
numbers simpler to see the operation · Jon sold 10 frogs.
Mike sold 2 frogs. o How many total frogs did they sell? → 10 + 2 = 12 total frogs
o How many more frogs did Jon sell? → 10 – 2 = 8 more frogs
o How many times more frogs did Jon
sell? → 10 / 2 = 5 times
more
· Jon sold 3.6 105 frogs.
Mike sold 2 103 frogs. o How many total frogs did they sell? → 3.6 105 + 2 103
= 362,000 total frogs = 3.62 105 total
frogs o How many more frogs did Jon sell? → 3.6 105 - 2 103
= 358,000 more frogs =
3.58 105 more frogs o
How many times
more frogs did Jon sell? → 3.6 105 / 2 103
= 180 times more = 1.8 102 times more For further
explanation on scientific notation word problems:


![]() is used to represent the new decimal location.
is used to represent the new decimal location.

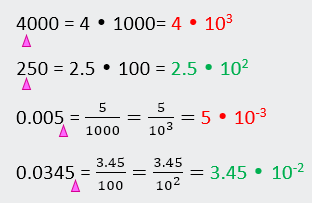
![]() → 8
103 = 8,000
→ 8
103 = 8,000
![]() → 4.321 105 =
432,100
→ 4.321 105 =
432,100
![]() → 1.5 x 10-2 = 0.015
→ 1.5 x 10-2 = 0.015 ![]() → 8.321 x 10-4 =
0.0008321
→ 8.321 x 10-4 =
0.0008321


![]() (2.8
x 10^6) /
(2 x 10^2) = 1.4 x 104
(2.8
x 10^6) /
(2 x 10^2) = 1.4 x 104

![]() → 2.8E6/2E2
→ 2.8E6/2E2