Systems of
Equations

Unit Overview
In this unit, students will be able
to:
·
Check
solutions for a system of equations
·
Solve a system
of equations by graphing
·
Identify the
number of solutions for a system of equations
·
Use system of
equations with word problems
Key Concepts
·
Systems of
equations
·
Parallel lines
Ohio’s Learning Standards
·
8.EE.8 Analyze and solve pairs of simultaneous linear
equations graphically.
o
a. Understand that the solution to a pair of linear equations
in two variables corresponds to the point(s) of intersection of their graphs,
because the point(s) of intersection satisfy both equations simultaneously.
o
b. Use graphs to find or estimate the solution to a pair of
two simultaneous linear equations in two variables. Equations should include
all three solution types: one solution, no solution, and infinitely many
solutions. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x +
2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6.
o
c. Solve real-world and mathematical problems leading to
pairs of linear equations in two variables. For example, given coordinates for
two pairs of points, determine whether the line through the first pair of
points intersects the line through the second pair. (Limit solutions to those
that can be addressed by graphing.)
Calculators
·
Here is a link
to the Desmos scientific calculator that is provided for the Ohio State
Test for 8th Grade Mathematics in the spring.
·
You are
strongly encouraged to use the Texas Instruments TI-30XIIS handheld scientific
calculator. It is extremely user
friendly.
System of Equations
·
A system of equations is a set of two
or more linear equations.
o The solution is any ordered pair that makes both equations true.
Example A: Find the solution for this system of
equations:
x
+ y = 6
x
– y = 2
Each equation has an infinite number of solutions.
x + y = 6 x
– y = 2
|
x |
y |
|
X |
Y |
|
0 |
6 |
|
-1 |
-1 |
|
1 |
5 |
|
2 |
0 |
|
2 |
4 |
|
3 |
1 |
|
3 |
3 |
|
4 |
2 |
|
4 |
2 |
|
5 |
3 |
|
5 |
1 |
|
6 |
4 |
|
6 |
0 |
|
7 |
5 |
|
7 |
-1 |
|
8 |
6 |
o
There is just one ordered pair that is a solution for both equations: (4, 2). That point is the solution for this system of
equations.
o
Let’s graph the solutions (points) of both equations.
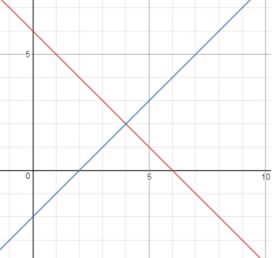
o
Notice that the lines cross at the solution, (4,
2).
·
The solution to any system of
equations is the point where their graphed lines cross.
·
To check a solution, substitute (x,
y) into both equations.
o
Both equations must produce true statements
o
Let’s check the solution for Example A, (4,
2).
x + y = 6 → 4 + 2 = 6
x – y = 2 4 – 2 = 2
Example B: Solve this system of
equations:
2x + 4y = 20
y
= 3x – 2
§ Let’s graph each
line by finding 2 points that are solutions, and then drawing a line through
those points.

§ We can also graph
either using the slope-intercept form: y = mx + b.
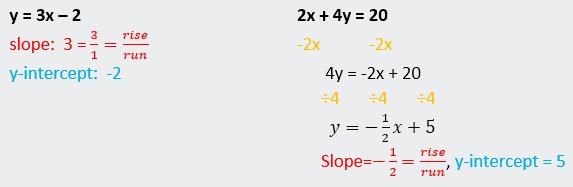
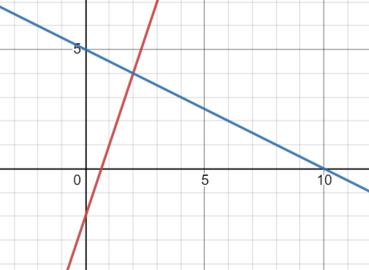
Let’s
check the solution, (2, 4) by substituting the coordinates into both
equations.
2x
+ 4y = 20 → 2 • 2 + 4 • 4 = 20 → 4 + 16 = 20
→ TRUE
y
= 3x – 2 4 = 3 • 2 – 2 → 4 = 6 – 2 → TRUE
For further
explanation and practice on graphing system of equations:
Let’s Practice.
Parallel
lines
·
Parallel lines have no solutions → they never cross,
and thus have no points in common.
o
Parallel lines have the same
slope (and a
different y-intercept). If they are in
slope-intercept form, you can quickly identify parallel lines.
o
Example C: Solve this system of equations:
y
= ½ x + 6
y = ½ x – 2
§ Use the slope intercept form to graph each line.
y = ½ x +
6 → slope =
½ , y-intercept = 6
y = ½ x – 2 → slope = ½ , y-intercept = -2
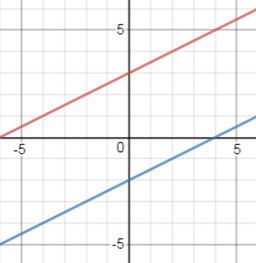
o
Both equations have a slope of ½ (with different y-intercepts).
o
When graphed, you see the parallel lines. Thus, the answer for this system is no
solutions.
o
Some parallel lines may not be in slope-intercept form, so you will
not be able to identify the equal slopes from the equations.
o
Example D: Solve this system of equations:

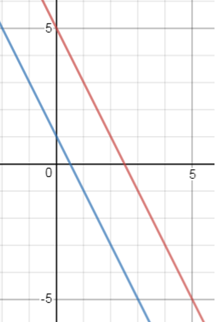
o
When graphed, these parallel lines both have a slope of -2. Thus, the answer for this system is no
solutions.
Identical
lines
· Identical
lines have infinite solutions: they have every point in common.
o They usually are
written in different forms, so the equations do not appear to be identical.
o
Example E: Solve this system of equations:
y = 3x – 6 → slope = 3, y-intercept
= -6
6x – 2y = 12
-6x -6x
-2y = 12 – 6x
÷-2 ÷-2 ÷-2
y
= -6 + 3x → slope = 3, y-intercept
= -6
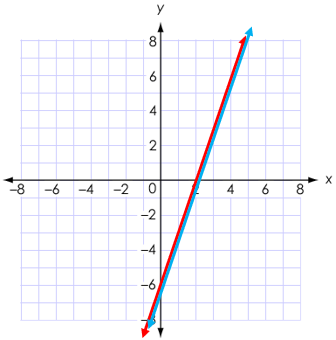
o
The equations produce identical lines.
Thus, there are infinite solutions.
For a further
explanation on number of solutions for systems:
Let’s practice.
System of
Equations Word Problems
·
If a word problem gives you a system of equations, simply graph them
and find the point of intersection. Be
sure to answer what the question is asking for.
·
If you need to write a system of equations from a word problem:
o
Identify your variables
o
Identify your rate(s) of change,
§ If there is just
one rate of change, it is often the slope (m).
§ It is usually multiplied by one or both
variables.
o
If you are given a starting value, that is usually your y-intercept
(b).
o
If given a slope and y-intercept into the equation, y = mx + b
o
Identify the total, which is usually a number or a variable.
Example F:
At “Cory’s Health Club”, you must pay
an initial $80 fee, as well as $30 per month.
George’s Gym costs $35 per month with no membership fee.
Part A: Write
a system of equations showing the relationship between the number of months as
a member (M) and the total membership cost (T) for both places. Then find the number of months when the costs
are equal.
·
Create
your equations using the variables T and M:
o Corey’s Health Club: T =
30M + 80 → $30 per month, plus a one-time $80 fee
o George’s Gym: T = 35M → $35 per month, no fee
Part B: At how
many months are the costs of the two gyms equal?
A. 12 months B. 16 months C. 20 months D. 24 months
·
You
could graph these, but it is hard to be precise with such large numbers. If you plug in the answers for both
equations, you will find that 16 months
produces the same cost:
o Corey’s Health Club: T =
30M + 80 → T = 30 • 16 + 80 =
$560
o George’s Gym: T = 35M → T = 35 • 16 = $560
Example G:
120 tickets
were sold for the school play. Adult
tickets (A) cost $8 each. Student
tickets (S) cost $3 each. Total ticket sales were $720.
Part A: Write a system for this scenario
·
Create
your equations using the variables A and S:
o 120 total tickets sold (adults +
students): A + S = 120
o $720 of tickets sold(adult
sales + students sales): 8A + 3S = 720
Part B: What are the number of tickets sold?
A. 72 adult tickets and 48 student
tickets
B.
80 adult tickets and 20 student tickets
C. 45
adult tickets and 100 student tickets
D.
63 adult tickets and 57 student tickets
·
Check
the solutions with the equations.
o You can quickly eliminate B and C,
since they don’t add up to 120 tickets sold
o Answer A (72 adult tickets and 48 student tickets) is
the correct answer
§ A + S = 120 →72 + 48 =120 → true
§ 8A + 3S = 720 → 8 • 72 + 3 • 48 = 720 → true
o Answer D: the total cost is wrong → 8 • 63 +
3 • 57 = 675
·
You
could graph these, but it is hard to be precise with such large numbers.
o Here is what the graph looks like
using the Desmos graphing calculator that you will use in the Algebra I Ohio
State Test:
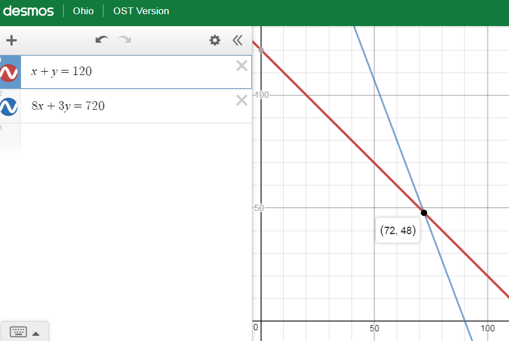
o They cross at 72, 48 à 72 adult tickets and 48 student
tickets.
For a
further explanation and practice on system word problems:
Let’s
practice.