Graphing Linear Functions


 

Unit Overview

In this unit, students will be able to:

·        graph linear functions in slope-intercept and standard form by finding solutions

·        identify solutions for 2-variable functions

·        graph one variable equations

Key Concepts

·        graphing solutions for linear functions

Connection to previous units

·        Unit 6:  Functions → Linear Functions

·        Unit 7:  Proportional Relationships → Linear Functions

Ohio’s Learning Standards

·        8.F.2 Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change.

·        8.F.4 Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values

Calculators

·        Here is a link to the Desmos scientific calculator that is provided for the Ohio State Test for 8th Grade Mathematics in the spring.

·        You are strongly encouraged to use the Texas Instruments TI-30XIIS handheld scientific calculator.  It is extremely user friendly.

 

Linear Function

·        A linear function is a two-variable equation (usually x and y) that forms a straight line when graphed

·        A linear function most commonly written in two forms:

o   Slope-intercept form (y =mx + b, where m and b are numbers), where y is by itself on one side of the equation.  Here are several examples

§  y = -5x                             

§  y = 2x + 3                             

§   

o   Standard form (Ax + By = C, where A, B, and C are numbers), where x and y are on the same side of the equation.  Here are several examples:

§  x + y = 6

§  2x + 4y = 10

§  x – 2y = 20

·        A solution to a linear function is any ordered pair that makes the equation true. 

·        A Linear function has an infinite number of solutions. 

·        The graphed line of a linear function is a visual representation of all of its solutions.

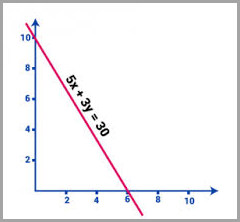
Example A:  Let’s look at an example:

o   x + y = 10

solutions

Checking the solutions for x + y = 10

(5, 5)

5 + 5 = 10

(2, 8)

2 + 8 = 10

(0, 10)

0 + 10 = 10

(12, -2)

12 + (-2) = 10

 

When graphing those solutions, notice that they form a straight line:



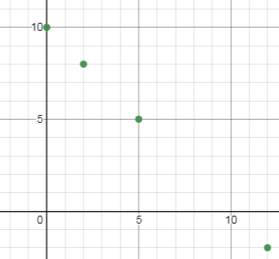
When graphing the entire equation, x + y = 10, a line shows every ordered pair solution that makes the equation true.  In this case, every ordered pair on the line adds up to 10, including ordered pairs with decimals like (7.5, 2.5).

 

 

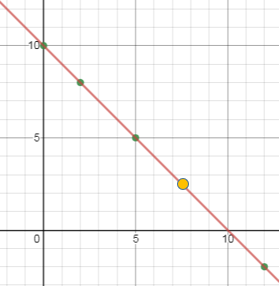
      Example B:  Let’s look at another example, this time in slope-intercept form:

o   y = 2x – 1

solutions

Checking the solutions for y = 2x – 1

(5, 9)

9 = 2•5 – 1

(1, 1)

1 = 2•1 – 1

(0, -1)

-1 = 2•0 – 1

(3, 5)

5 = 2•3 – 1


 

When graphing those solutions, notice that they form a straight line.

 

 

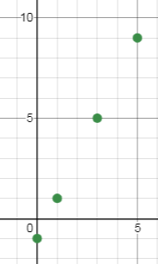
When graphing the entire equation, y = 2x − 1, a line shows every ordered pair solution that makes the equation true, including a ordered pairs with decimals like (2.5, 4).

     

 

 

 

 

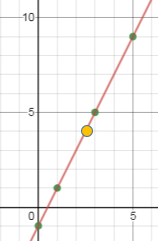
HOW TO GRAPH LINEAR EQUATIONS

·        The traditional algebraic process for graphing a linear function is:  

o   1st: Find at least two ordered pairs (points) that are solutions for the function (using an x-y table).

o   2nd: Graph those ordered pairs and draw a line through them.

·       Example C:   Graph this slope-intercept form function:      y = -4x + 6

1st:  find two points that are solutions. Since y is by itself, you should pick any number to put in for x, then solve for y.  I suggest using 0 and 1 for x:

x

y

0

?

1

?

 

y = -4•0+6  à   y = 6

y = -4•1+6  à   y = 2

x

y

0

6

1

2

 

2nd: graph those two points, then draw a line through them. 

 

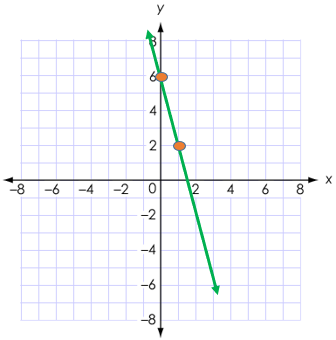
o   This line represents all solutions for y = -4x + 6

§  Solutions such as (2, -2), (3, -6), (1.5, 0) and (-1, 10) all fall on this line.

     

 

·    Example D:   Graph this slope-intercept form function: 

1st:  find two points that are solutions. Since y is by itself, you should pick any number to put in for x, then solve for y.  Since you have a fraction, I suggest you use 0, as well as the denominator of the fraction (to avoid getting a fraction answer to graph).

put in for x, then solve for y.  I suggest using 0 and 1 for x:

x

y

0

?

3

?

 

 

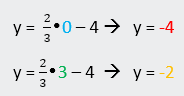
x

y

0

-4

3

-2

 

2nd: graph those two points, then draw a line through them. 


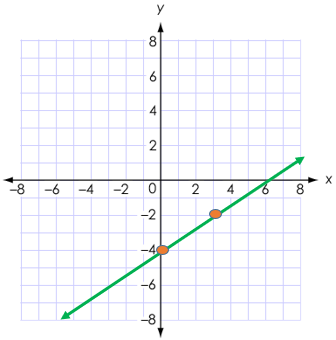
o    This line represents all solutions for  

§     Solutions such as and (6, 0) all fall on this line.

 

·      Example E:    Let’s look at a function in standard form:  2x + 4y = 12

o   First, find two points.  Since y is not by itself, I suggest putting in 0 for x, then solving for y. Then putting in 0 for y, then solve for x:

 

x

y

0

?

?

0

 

2x + 4y = 12

2•0 + 4y = 12 

            4y = 12

              y = 3

2x + 4y = 12

2x + 4•0 = 12 

            2x = 12

              x = 6

 

x

y

0

3

6

0

 

 

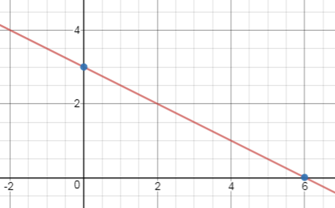
o   This line represents all solutions for 2x + 4y = 12

§  Solutions such as (1, 2.5), (2, 2), (3, 1.5) and (-2, 4) all fall on this line.

 

For a further explanation of graphing linear equations:

 

 

Let’s practice graphing equations. 




Checking Solutions

·        To check if an ordered pair is a solution to a function, you can either:

o   Graph the function, and see if the point is on the line

o   Substitute the ordered pair into the function and see if it makes the equation true.

Example F:    For the function,  which ordered pairs are solutions?

 

            A. (9, 12)                  B.  (8, 10)            

 

I first graphed the function, as well as the points.



You will notice that (9, 12) and are solutions since they are both on the line.  (8, 10) is not a solution, since it is not located on the line.    

We can also check if those ordered pairs are solutions by substituting the x and y values into the function:

 

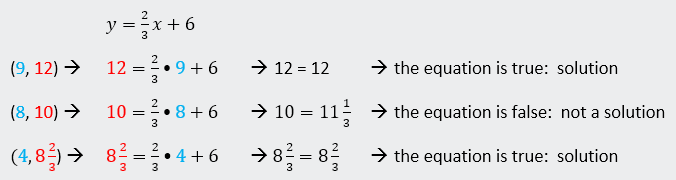
For a further explanation and practice on checking solutions for linear equations:

 

 

 

 

Let’s practice checking solutions for functions. 

 

 

 

 

 

 

Graphing One-Variable Equations:  linear equations sometimes use just one variable. 

Example G:    Graph  y = 2

·        For this equation, there are no requirements of the x-coordinate, but all of the solution points on the line have 2 as a y-coordinate.  Here are a few:

 

 

 

 

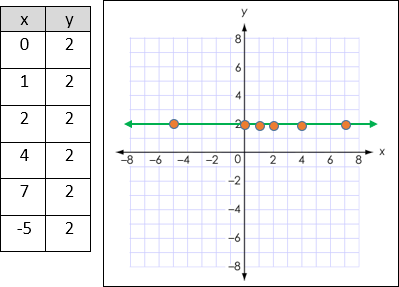
·        A shortcut for graphing y = 2 is to go to 2 on the y-axis and draw a horizontal line through it.

·        This equation is a function

o    each input (x) has just one output (y). 

o   No x-value has two different y-values.

o    It also passes the Vertical Line Test.

Example H:    Graph the equation, x = 4.

·        In this case, all the x-values must be 4. 

·        The y-values can be anything.



 

 

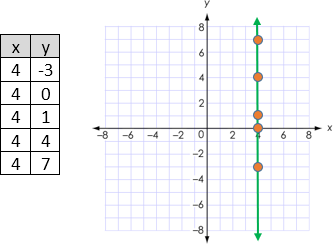
·        A shortcut for graphing x = 4 is to go to 4 on the x-axis and draw a vertical line through it.

·        This equation is NOT a function

o    one input (the x-value of 4) has multiple different outputs

o    This line also does not pass the vertical line test, since it is a vertical line.

 

 

For a further explanation on one-variable linear equations:


 



Let’s practice working with one-variable equations.