Integer
Operations
Unit Overview
In this
unit, students will be able to perform various operations with integers.
Key Concepts
·
Add, subtract, multiply, and divide integers
·
Apply order of operations
Ohio’s
Learning Standards
·
7.NS.1 Apply and extend previous understandings of addition and
subtraction to add and subtract rational numbers; represent addition and
subtraction on a horizontal or vertical number line diagram.
·
7.NS.2 Apply and extend previous understandings of multiplication and
division and of fractions to multiply and divide rational numbers.
Calculators:
·
Here is a link to the Desmos scientific calculator that is provided for the Ohio State Test for 8th
Grade Mathematics in the spring.
·
You are strongly encouraged to use the Texas Instruments TI-30XIIS
handheld scientific calculator. It is
extremely user friendly.
Introduction
The integer number set is defined as whole numbers and their opposites
…, -3, -2, -1, 0,
1, 2, 3, …
While
performing operations with integers is taught at earlier grade levels--and
calculator use is allowed at the 8th grade level, the understanding
of how integer calculations work is extremely important for many math concepts
in 8th grade and beyond.
Adding Integers
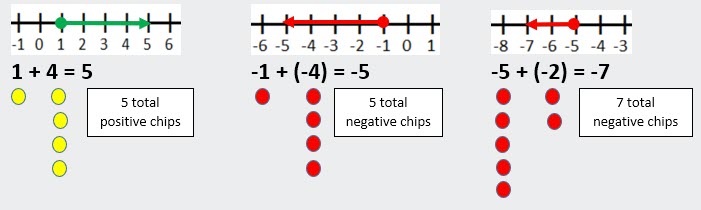
·
Example A Set: Same-signed numbers using integer chips and
number lines
 |
o
When adding same-signed numbers, total
them up (add)
·
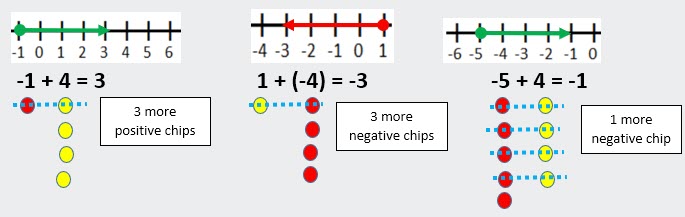
Example B Set: different-signed numbers using integer chips
and number lines
o
-1 + 1 = 0 → this is known as a zero pair. The opposites
cancel
→
![]()
 |
o
When adding different-signed numbers, cancel out zero pairs (subtract)
Click on the words Adding
Integers for a further explanation:
Subtracting
Integers → change to adding the
opposite
·
Example C Set: subtracting (taking away) positives → value decreases (goes down)
 |
§ You can change each
of these subtraction problems to adding the opposite:
5 – 2 = 3 -5 – 2 = -7 1 – 4 = -3
5 + (-2) = 3 -5 + (-2) = -7 1 + (-4) = -3
|
·
Example D Set: subtracting (taking away) negatives → value increases (goes up)
 |
§ You can change
these subtraction problems to adding the opposite:
-5 – (-2) = -3 4 – (-2) = 6 -1
– (-4) = 3
|
Click on
the words Subtracting
Integers for a further explanation:
Let’s
practice.
Multiplying Integers
§ EXAMPLE E Set: positive # • negative #
o
To show the resulting sign values, let’s re-write these problems as
addition.
-5 • 2 = -5 + (-5) = -10
-2 • 5 = -2 + (-2) + (-2)
+ (-2) + (-2) = -10
3 • (-7) = -7 + (-7)
+ (-7) = -21
o positive # • negative # → the answer is always negative
·
EXAMPLE F Set: negative # • negative #
o
Multiplying with 1 negative (like above) changes the answer sign a
negative
o
Multiplying with 2 negatives changes the answer sign back to a
positive.
-5 • (-7) = 35 -6 • (-1) = 6 -10 • (-6) = 60
o negative # • negative # → the answer is always positive
·
EXAMPLE G Set: multiplying any amount of negative numbers → partner up negative pairs to become positive
o
even number of negative numbers = positive answer
→ all negatives have
partner
o
odd number of negative
numbers = negative answer → one negative has
no partner
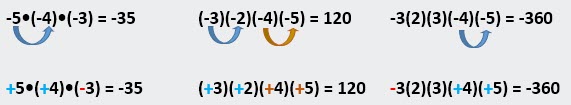 |
Dividing Integers → the exact same rules as multiplication (since in
earlier grades with fractions), we learned that any division can be re-written
as multiplication
§ EXAMPLE H Set:
Click on
the words Multiplying
and Dividing Integers for a further explanation:
Let’s
practice.
Using Order
of Operations → PEMDAS: “Please Excuse My Dear Aunt Sally”
| Parentheses → any grouping
symbols
|
| Exponents → we will cover this
topic in detail in a later unit
|
Multiply
|
Add
|
EXAMPLE I Set:
8 – 4(-6) = ? 5
– 2 + 3 = ? -4•5
- 3•2 = ? -3 + 4(2 – 5) = ?
8 – 4(-6) 5 – 2 +
3 -4•5 -
3•2 -3
+ 4(2 – 5)
8 – (-24) 3 + 3 = 6 -20 – 6 -3
+ 4(-3)
8 + (+ 24) = 32 -20
+ -6
= -26 -3
+ (-12) = -15
Click on
the words Order
of Operations for a further explanation:
Let’s practice.