MATRICES

Unit Overview

Matrices can neatly organize and store data that is represented in a table. This unit will teach you how you can use matrices to display data from a table and how you can manipulate data using matrices. You will learn to add, subtract, and multiply matrices.

Matrices

A matrix is an array of numbers represented with horizontal rows and vertical columns, which represent the dimensions of the matrix.

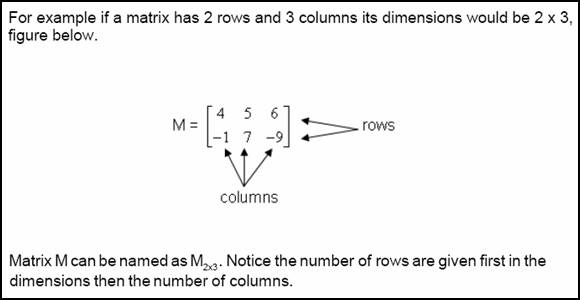
Each number in a matrix is known as an entry or element. Each entry has an address or location in a matrix and is denoted by the row number and the column number. In matrix M above, the entry 6 has an address of row 1 column 3 and can be written as m₁₃.

Now take a look at how data from a table can be written using a matrix. The given table represents a clothing store’s inventory of a brand of t-shirts and sweatshirts. It includes sales and re-orders for the month of May. We are going to represent the May inventory data in a matrix.

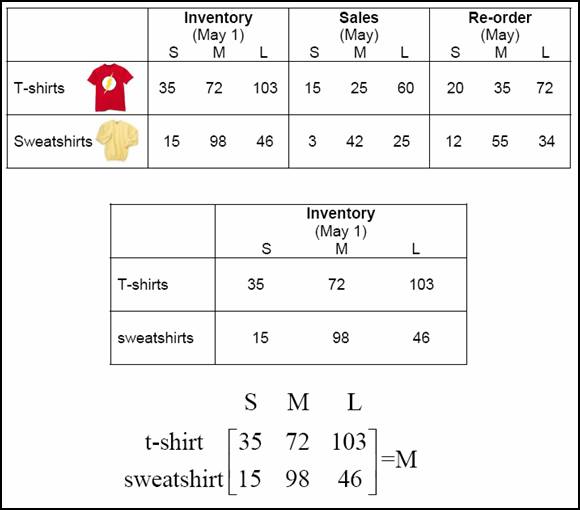
In matrix M above if you locate m₂₃, you will see that it is equal to 46 because the number that is in row 2 column 3 is 46. This means that in May, 46 large sweatshirts were in the store.

Adding and Subtracting Matrices

Matrices can be added or subtracted if they have the same dimensions. Each element of one matrix is added to or subtracted from the corresponding element of another matrix.

In the table we used for the t-shirts and sweatshirts we can use matrices to determine the number of t-shirts and sweatshirts the store has in stock after the May sales and reorders.

We will label the inventory matrix I, the sales matrix S, and the re-order matrix R. If we subtract the sales from the inventory and then add the re-orders, we will have the total number of small, medium, and large t-shirts and sweatshirts the store has left at the end of the month.

Multiplying Matrices

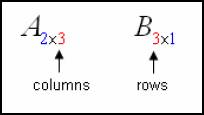
Matrices can be multiplied together if the number of columns of the first matrix match the number of rows in the second matrix.

Let’s take a closer look at how this works. Since the number of columns in matrix A (3) match the number of rows in matrix B (3), we can multiply the two matrices together. The resulting matrix will have dimensions of 2 x 1, which are the numbers left from the dimensions.

To multiply matrices, you will multiply the entire first row of matrix A with each of the elements in matrix B. Each product will be added together to produce the elements in the product matrix. Follow along with the example below.

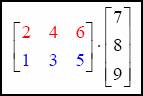
Multiply the first row 2, 4, 6 with the column 7, 8, 9. What you will do is match the elements of row 1 with the elements in the column.

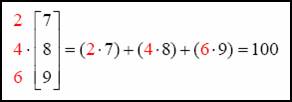
Do the same thing with the second row.

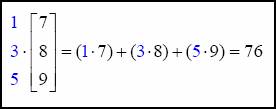
Now put it all together.

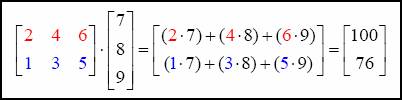
Look at how multiplying matrices can be used in our t-shirt and sweatshirt store. We are going to find out how much money the store made on the t-shirts and sweatshirts. We will do this by multiplying the sales matrix by another matrix representing the cost of each small, medium, and large shirt.

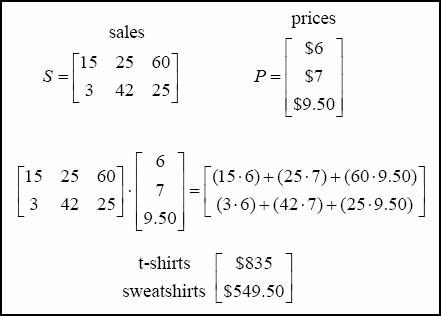
The total revenue made from the t-shirts and sweatshirts was $835 and $549.50 respectively.

Below are additional educational resources and activities for this unit.

Unit 12 Matrix Basics Worksheet

Unit 12 Matrix Multiplication Worksheet

Unit 12 Matrix Multiplication Worksheet