COMBINATIONS AND PERMUTATIONS

Unit Overview
This unit will introduce you to nutritional facts that represent a balanced diet. Using these facts, you will use combinations and permutations to determine how many different meals can be arranged.
Combinations
A well-planned meal or balanced diet gives you all the nutrients you need each day. To plan a balanced diet, you need to select foods from each of the main food groups. The food pyramid below is a practical tool to help you make food choices that are consistent with the Dietary Guidelines for Americans. The color-coded stripes are different widths to show how much of a person's daily food intake should be made up of that food group. Notice that the orange band (grain) is much wider than the yellow one (oil) because people need to eat many more grains than fats and oils.

To make the most of the pyramid you need to know what makes up a serving.
|
What
makes a serving? |
|
|
Vegetables |
1 cup raw, leafy vegetables ½ cup cooked or chopped raw
vegetables ¾ cup vegetable juice |
|
Grains |
1 slice of bread ½ bagel or English muffin 1 ounce ready-to-eat cereal ½ cup cooked cereal, rice, or
pasta 5-6 small crackers |
|
Fruits |
1 medium piece of fruit ½ cup mixed fruit ¾ cup fruit juice |
|
Milk |
1 cup milk or yogurt 1½ ounces natural cheese 2 ounces processed cheese |
|
Meat & Beans |
2-3 ounces cooked lean meat,
poultry, or fish (about the size of a deck of cards) ½ cup cooked dry beans 1 egg 2 tablespoons peanut butter 1/3 cups nuts |
Now that you are familiar with the nutritional aspect of your diet, let’s take a look at going to the grocery store and finding the best buy on some food that will produce a well-balanced meal. We are going to use the example of a girl named Hanna who is planning a dinner for some friends. She wants to make sure that her dinner includes foods from all the food groups and that her guests have a choice of meals. Hanna also wants to make sure that she is getting the best buy at the grocery store.
To determine if she is getting the best buy at the grocery store, Hanna must do some mathematics to determine the unit price of each of her items. To find the best buy, she will have to make comparisons, called ratios, using the price and the unit of food. She will then have to find the unit rate by reducing the ratio until the denominator is equal to 1.
| Example 1: |
 |
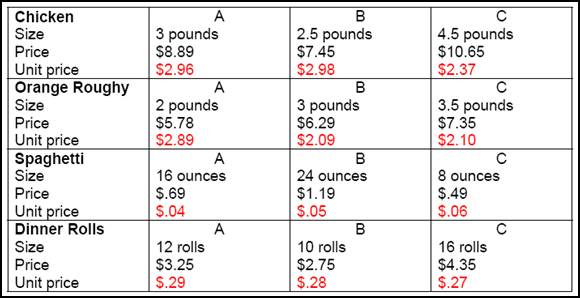
Now let’s take a look at Hanna’s grocery list and help her find the best buy for some of the items on her list below.

The chart below shows the unit prices for the items on Hanna’s list. There are three different sizes given for each item. The unit prices are listed in red.
Now look at the different types of foods Hanna has for her friends and separate them into the food groups:
|
Vegetables |
spaghetti sauce, lettuce |
|
Grains |
spaghetti, brown rice, crackers,
dinner rolls |
|
Fruits |
mixed fruit, peaches |
|
Milk |
milk, cheese |
|
Meat & Beans |
chicken, fish, mixed nuts |
If Hanna wants to know how many combinations of total possible meals she has, she will multiply the number of each type as shown below:
|
Number of vegetables |
x |
Number of dairy |
x |
Number of grains |
x |
Number of fruits |
x |
Number of meats |
= |
Total possible meals |
|
2 |
x |
2 |
x |
4 |
x |
2 |
x |
3 |
= |
96 |
Hanna could plan 96 different meals.
This example is an introduction to combinations, an arrangement of objects in which order is not important. Such situations may occur when choosing members for a committee, numbers drawn for bingo, or determining your chances of winning the lottery. The following formula for combinations is given below.
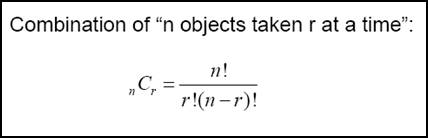
To understand this formula, you need to understand the symbolism. The symbol ! is a mathematical expression called factorial. This means that for an integer n, n! means to multiply all integers 1, 2, 3, 4, …, n together to produce a result called n factorial.
| Example 2 and Example 3: |
 |
That brings us back to our original formula.
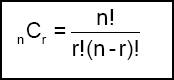
The n represents the number of things that are available. The r represents the number of things you are choosing.
| Example 4: |
 |
Sometimes you will need to find combinations of more than one thing at a time. In this case, what you want to do is multiply the combinations together to find the total number of combinations.
Let’s go back to the pizza example and add some cheese toppings to the list of choices. Follow the example below.
| Example 5: |
 |
Permutations
Another way of arranging objects is called permutations. A permutation is an arrangement of objects in a specific order. Such arrangements could include the batting order of a softball team, seating arrangements of students in a classroom, or the arrangements in a store display. The following is the formula for finding the number of permutations of n objects taken r at a time.
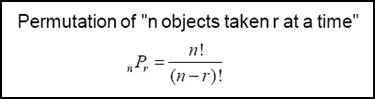
| Example 6: |
 |
To learn more about combinations and permutations, watch the video below.
 |
| Unit 11 Permutations vs Combinations Worksheet |
| Unit 11 Permutations and Combinations Worksheet |