CIRCLES
ARCS AND CENTRAL ANGLES
|
Unit Overview
In this unit, students will identify and describe relationship among central angles and arcs.
Key Vocabulary
Arcs and Central Angles
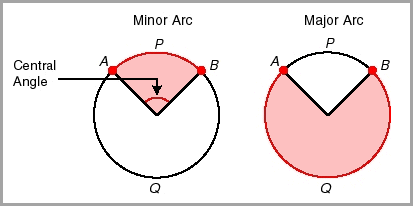
An angle whose vertex is at the center of a circle is called a central angle. A central angle separates a circle into two arcs called a minor arc and a major arc. In the circle above, ÐAPB is the central angle.
An arc is a section of a circle. The semicircle is an arc that measures 180°. A minor arc is smaller than a semicircle and a major arc is larger than a semicircle.
A minor arc is composed of two endpoints on the circle and the points on the circle that are on the interior of its central angle. In the circles above, points A and B and all points of the circle interior to ÐAPB form a minor arc called arc AB. The measure of the minor arc is equal to the measure of its central angle.
A major arc is composed of two endpoints and the points on the circle that are not on interior of the central angle. In the circle above, points A and B and all points of the circle exterior to ÐAPB form a major arc called arc AQB. The measure of a major arc is equal to 360° minus of its central angle.
A semicircle is an arc whose endpoints are the endpoints of a diameter of a circle. The measure of a semicircle is 180°.
Click on the link to watch a video on Intro to Arc Measures.
Hint: When given two letters it will be the minor arc and when given three letters it will be the major arc.
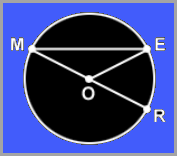
Let's Practice - Vocabulary Identification
Use Circle O below to identify the correct vocabulary word that describes each of the following figures. Use the Key Vocabulary list in the beginning of the unit.
 |
|
 Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
|
Move the mouse cursor over the figure to check the answer. |
Minor and Major Arcs
A central angle is the angle formed by two radii with its vertex at the center of the circle. A minor arc is an arc that is greater than 0° and less than 180°. A major arc is an arc that is greater than 180° and less than 360°.
Put this in practice by clicking on the word Arc to identify the difference between a major and minor arc. Once, you practice recognizing the differences click on the word Calculate to measure the minor and major arcs of a circle.
Let's Practice - Minor and Major Arcs
Identify each arc as either major arc, minor arc, or semicircle.
Segment BD and AC are diameters of circle O.
 |
|
|
|
|
| Move the mouse cursor over the figure to check the answer. |
11.) Find the measure of arc AXB.
|
| Move the mouse cursor over the figure to check the answer. |
12.) Find the value of x°.
|
| Move the mouse cursor over the figure to check the answer. |
Central Angle Properties
Look at the figure below and the properties of central angles and arcs.
 |
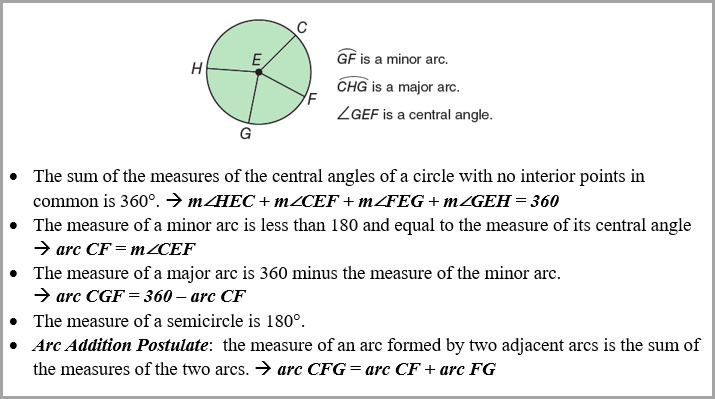Click on the words Central Angle Properties to watch a video demonstration on the measures of arcs.
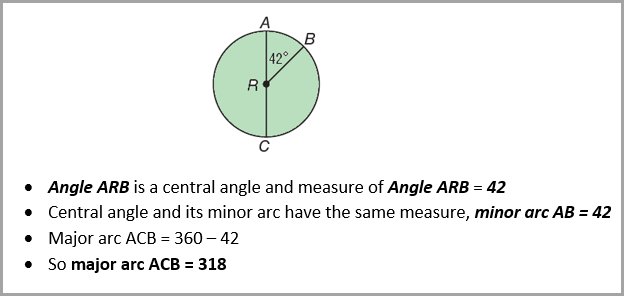
Example A - Find minor arc AB and major arc ACB.
Segment AC is a diameter of circle R.
 |
Example B - Find minor arc OK.
 |
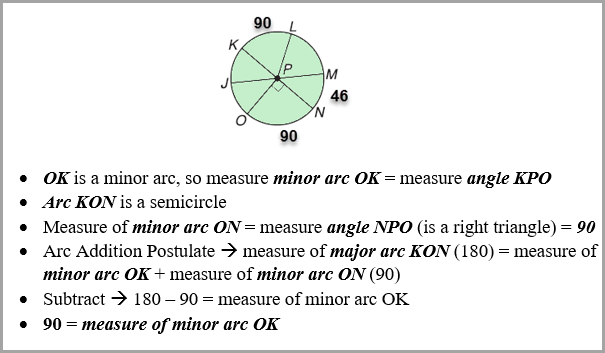Let's Practice - Central Angle Relationships
13.) Segment AC is a diameter. Find the measure of minor arc BC.
|
| Move the mouse cursor over the figure to check the answer. |
14.) Find the measure of major arc JKO.
|
| Move the mouse cursor over the figure to check the answer. |
15.) Find the measure of minor arc RT.
|
| Move the mouse cursor over the figure to check the answer. |
16.) Find the measure of major arc TSR.
|
| Move the mouse cursor over the figure to check the answer. |
Summary - Arcs and Central Angles
Arcs are sections of a circle. The letters used to label an arc are the points on the circle. There are three main types of arcs.
 |
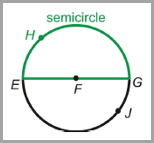minor arc BC and major arc BDC |
The central angle divides the circle into two arcs: either two semicircles or one major arc and one minor arc.
Arc Addition Postulate: The measure of the arc formed by two adjacent arcs is the sum of measure of the two arcs. BC and CD are adjacent arcs. Arc CDB = Arc CD + Arc DB
Let's Practice - Summary
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
|
| Move the mouse cursor over the figure to check the answer. |
 |
|
 Click on the icon to the left to watch a video and complete a quiz on Circles. |
 Click on the icon to the left to watch a video explanation of a Radius, Diameter, Circumference and Pi. |
|
| Practice 2: Central Angles and Arcs |
